⚡ こんな疑問を持っていませんか?
- 「抵抗率ρ」と「導電率σ」って何が違うの?
- 単位の「Ω・m」と「S/m」の意味がよくわからない…
- 電験三種の問題でρとσを使い分けられない!
- 温度で抵抗が変わるのはなぜ?
💡 この記事でわかること
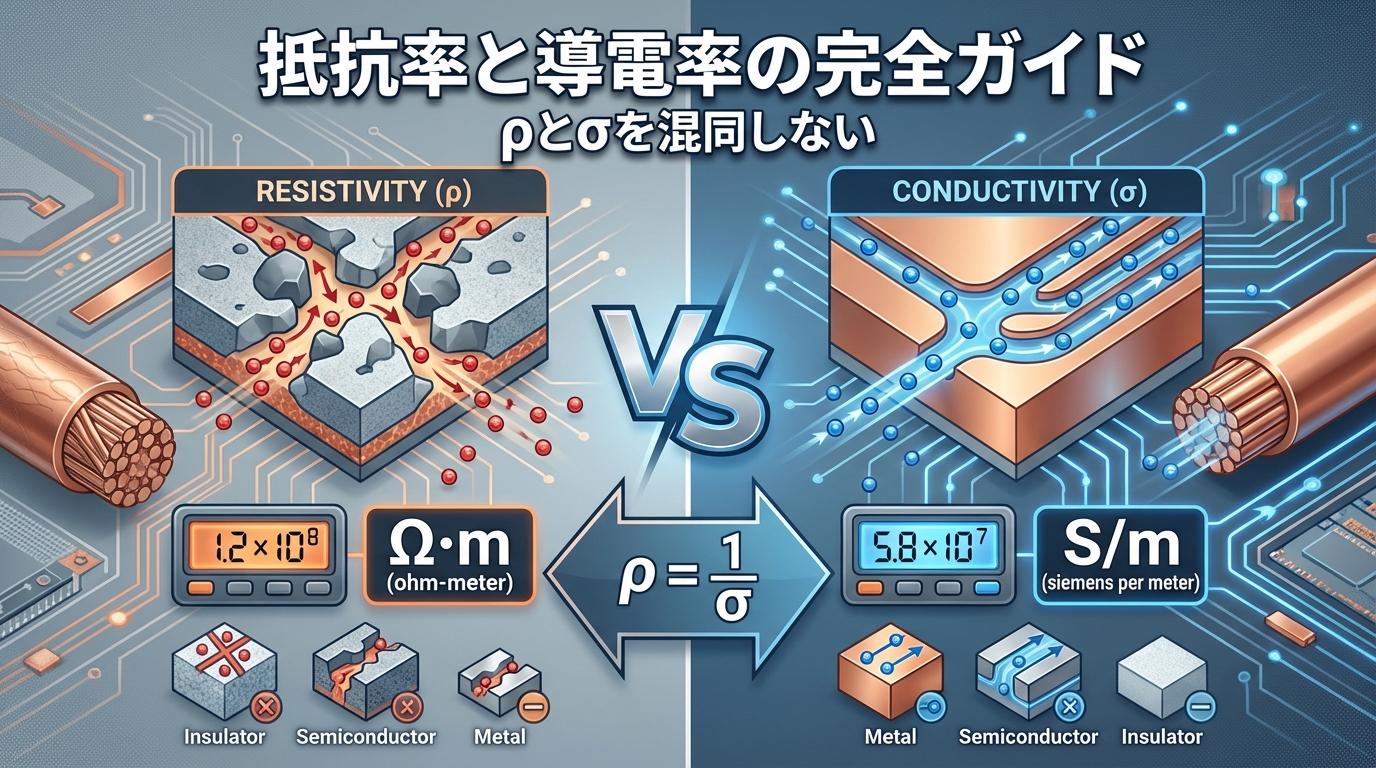
抵抗率ρ(オーム・メートル)と導電率σ(ジーメンス毎メートル)は、材料の電気特性を表す「表裏一体の関係」です。ρは「電気の流れにくさ」、σは「電気の流れやすさ」を示し、σ = 1/ρという逆数の関係にあります。
この記事では、初心者でも絶対に混同しないように、単位の意味から温度の影響、実務での使い分けまで、図解でわかりやすく解説します!
目次
1️⃣ 抵抗率ρと導電率σの基本的な違い
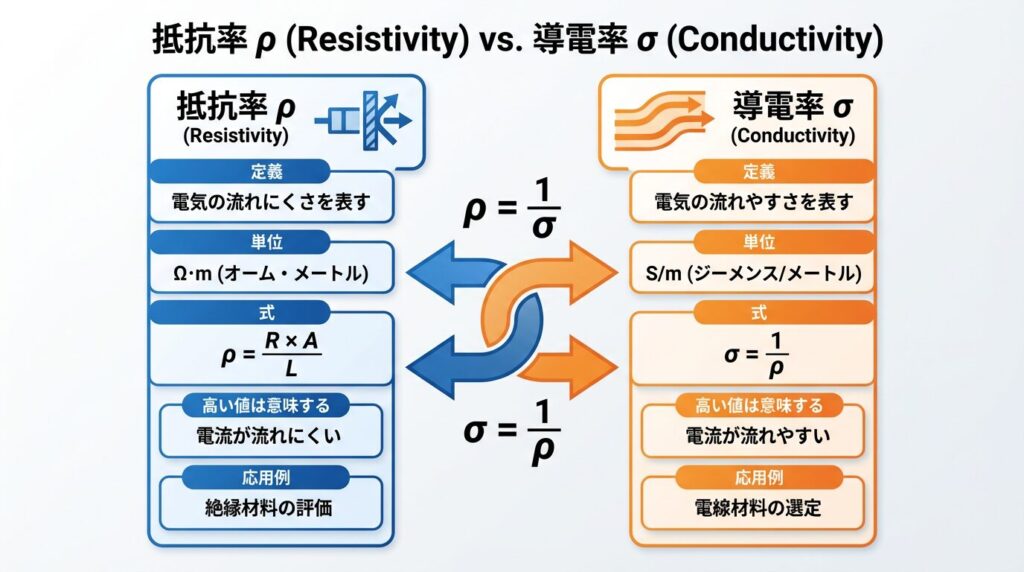
🔍 抵抗率ρ(Resistivity)とは?
抵抗率ρ(ロー)は、「材料が電流をどれだけ通しにくいか」を表す指標です。
📏 単位: Ω・m(オーム・メートル)
📊 数値の意味: 値が大きいほど電気を通しにくい(絶縁体ほど大)
🧮 公式: ρ = R × A / L
※ R:抵抗(Ω)、A:断面積(m²)、L:長さ(m)
⚡ 導電率σ(Conductivity)とは?
導電率σ(シグマ)は、「材料が電流をどれだけ通しやすいか」を表す指標です。
📏 単位: S/m(ジーメンス毎メートル)
📊 数値の意味: 値が大きいほど電気を通しやすい(導体ほど大)
🧮 公式: σ = 1 / ρ
※ 抵抗率の逆数
🔄 ρとσの関係性(超重要!)
σ = 1 / ρ または ρ = 1 / σ
抵抗率と導電率は「逆数の関係」にあります。つまり:
✅ 抵抗率ρが大きい材料 → 導電率σは小さい(電気を通しにくい)
✅ 抵抗率ρが小さい材料 → 導電率σは大きい(電気を通しやすい)
同じ材料の特性を、見方を変えて表現しているだけなのです!
💡 実務での使い分けポイント
| 使用する場面 | 使う指標 | 理由 |
|---|---|---|
| 絶縁材料の評価 | 抵抗率ρ | 値が大きいほど性能良好 |
| 電線材料の選定 | 導電率σ | 値が大きいほど性能良好 |
| 半導体材料の研究 | どちらも使用 | 文脈により使い分け |
🔗 関連記事:
📖 統計の基礎知識│データ分析の第一歩
📖 電験三種「理論」科目攻略法
📖 YouTubeで電験三種を制する独学インプット法
2️⃣ 単位の意味を完全理解│Ω・mとS/mの正体
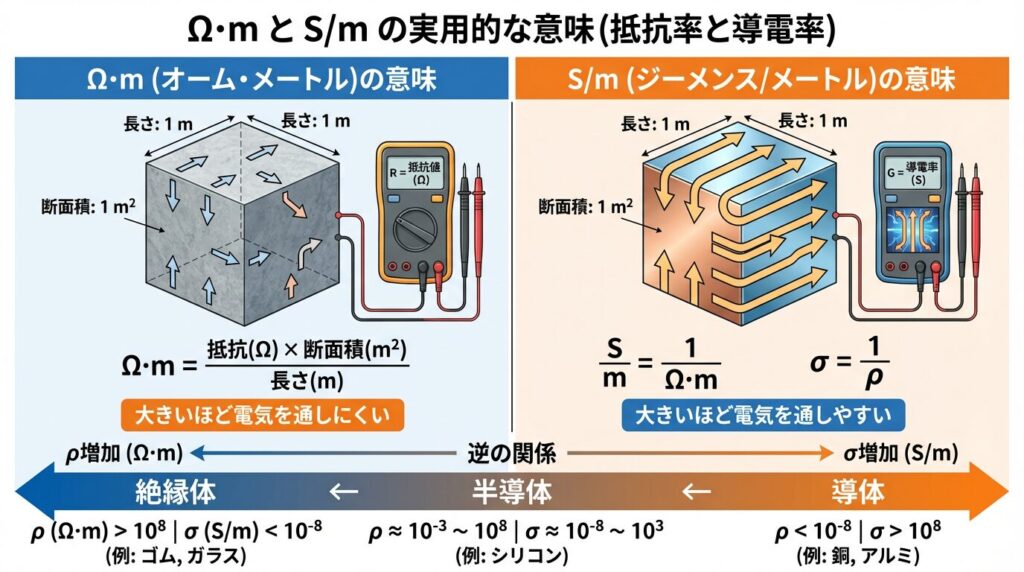
📏 Ω・m(オーム・メートル)の意味
抵抗率の単位「Ω・m」は、「1m³の立方体材料の対向する面間の抵抗値」を表します。
🧮 公式の詳細:
ρ = R × A / L
➡ R = ρ × L / A
具体例で考えると:
• 断面積A = 1m²
• 長さL = 1m
の材料の抵抗Rが、その材料の抵抗率ρ[Ω・m]になります。
※ 実際には非常に大きな断面積なので、現実的には小さなサンプルで測定してρを算出します
📏 S/m(ジーメンス毎メートル)の意味
導電率の単位「S/m」は、抵抗率の逆数単位で、「1m³の立方体材料の導電性の高さ」を表します。
📚 単位の関係:
• S(ジーメンス) = 1/Ω(コンダクタンス)
• σ[S/m] = 1 / ρ[Ω・m]
覚え方のコツ:
✅ S(ジーメンス)は「抵抗の逆数」を表す単位
✅ だから導電率σ = 1/ρ も「抵抗率の逆数」
✅ 単位も値も、すべて「逆数の関係」で統一されています!
🔢 単位換算の具体例
例題:銅の抵抗率と導電率
【与えられた値】
銅の抵抗率: ρ = 1.68 × 10⁻⁸ Ω・m
【導電率を求める】
σ = 1 / ρ
σ = 1 / (1.68 × 10⁻⁸)
σ = 5.95 × 10⁷ S/m
つまり、銅は「約6000万S/m」という高い導電率を持つ優秀な導体!
🔗 関連記事:
📖 電験三種「理論」科目の計算問題攻略法
📖 電験三種の公式暗記術
📖 電験三種とは?資格の全体像
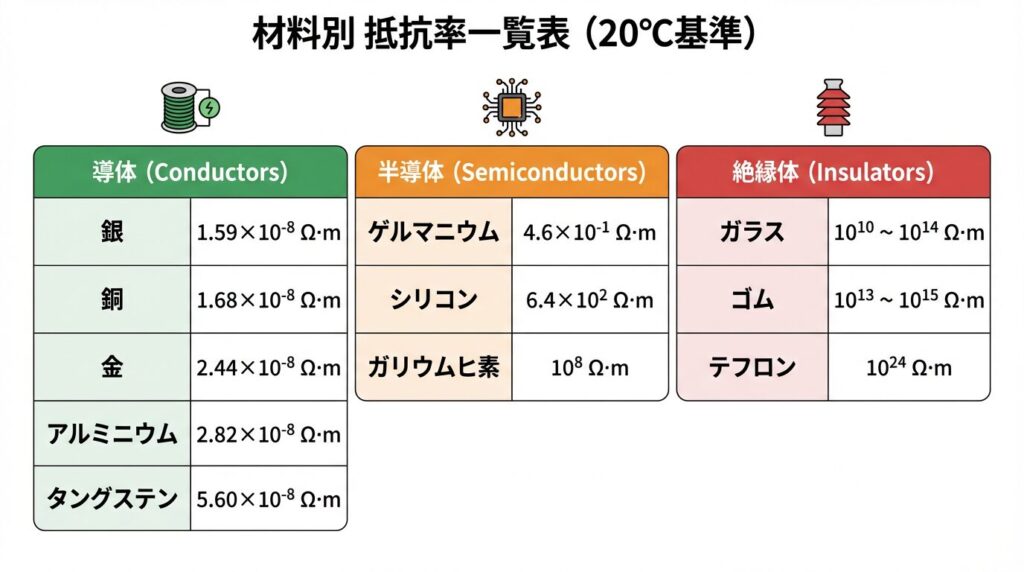
3️⃣ 材料別の抵抗率一覧表(20℃基準)
⚡ 導体(Conductors)の抵抗率
導体は抵抗率が極めて小さい(10⁻⁸ Ω・mオーダー)のが特徴です。
| 材料 | 抵抗率ρ[Ω・m] | 特徴・用途 |
|---|---|---|
| 銀(Ag) | 1.59 × 10⁻⁸ | 最高の導電性/高価 |
| 銅(Cu) | 1.68 × 10⁻⁸ | 電線の標準材料 |
| 金(Au) | 2.44 × 10⁻⁸ | 耐食性に優れる/接点 |
| アルミニウム(Al) | 2.82 × 10⁻⁸ | 軽量/送電線 |
| タングステン(W) | 5.60 × 10⁻⁸ | 高融点/電球フィラメント |
🔶 半導体(Semiconductors)の抵抗率
半導体は導体と絶縁体の中間の抵抗率を持ち、温度やドーピングで大きく変化します。
| 材料 | 抵抗率ρ[Ω・m] | 特徴・用途 |
|---|---|---|
| ゲルマニウム(Ge) | 4.6 × 10⁻¹ | 初期のトランジスタ材料 |
| シリコン(Si) | 6.4 × 10² | 現代半導体の主役 |
| ガリウムヒ素(GaAs) | 10⁸ | 高速デバイス/LED |
🛡️ 絶縁体(Insulators)の抵抗率
絶縁体は抵抗率が極めて大きい(10¹⁰ Ω・m以上)のが特徴で、電流をほとんど通しません。
| 材料 | 抵抗率ρ[Ω・m] | 特徴・用途 |
|---|---|---|
| ガラス | 10¹⁰ ~ 10¹⁴ | 電気絶縁・光学用途 |
| ゴム | 10¹³ ~ 10¹⁵ | 電線被覆材 |
| テフロン | 10²⁴ | 最高級の絶縁性 |
💡 覚えておくべき数値:
• 銅の抵抗率: 約1.7 × 10⁻⁸ Ω・m(電験頻出!)
• アルミの抵抗率: 約2.8 × 10⁻⁸ Ω・m(送電線で重要)
• 銀>銅>金>アルミの順で導電性が高い(抵抗率が低い)
• 半導体は温度で抵抗率が大きく変わる!
🔗 関連記事:
📖 電験三種「電力」科目攻略│送電線の材料選定
📖 電験三種「機械」科目攻略│半導体の基礎
📖 電験三種「理論」科目の頻出分野
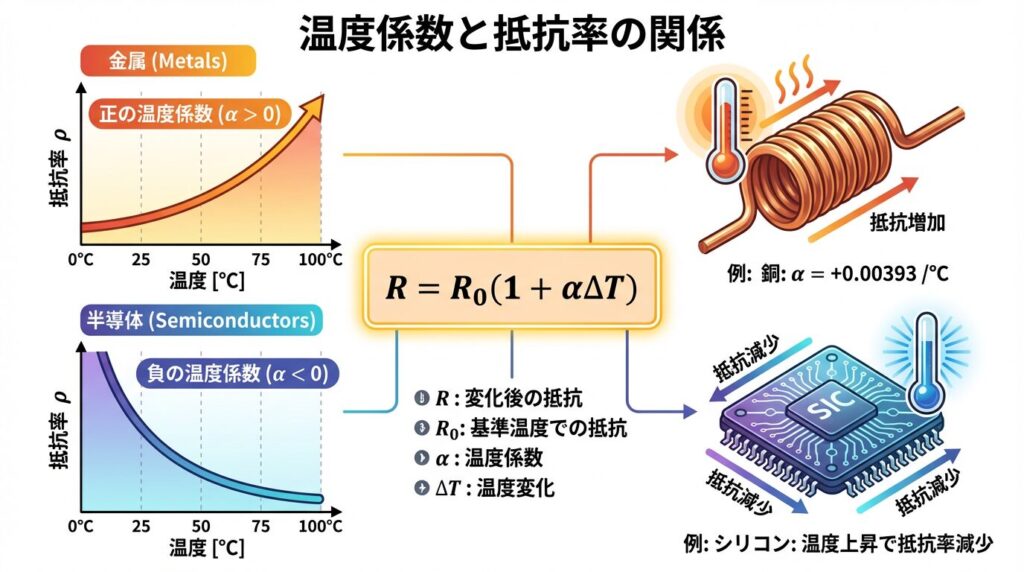
4️⃣ 温度係数と抵抗の変化
🌡️ 温度係数α(アルファ)とは?
温度係数αは、「温度が1℃上昇したときの抵抗率の変化率」を表す指標です。
🧮 温度による抵抗変化の公式:
記号の意味:
• R: 温度変化後の抵抗[Ω]
• R₀: 基準温度(通常20℃)での抵抗[Ω]
• α: 温度係数[/℃]
• ΔT: 温度変化[℃] (= T - T₀)
🔥 金属(正の温度係数)
金属は温度が上がると抵抗率が増加(α > 0)します。これは「正の温度係数」と呼ばれます。
| 材料 | 温度係数α[/℃] | 20℃→100℃で |
|---|---|---|
| 銅(Cu) | +0.00393 | 抵抗が約31%増加 |
| アルミ(Al) | +0.00403 | 抵抗が約32%増加 |
| タングステン(W) | +0.0045 | 抵抗が約36%増加 |
💡 理由: 温度上昇で金属原子の熱振動が激しくなり、電子が流れにくくなるため。
❄️ 半導体(負の温度係数)
半導体は温度が上がると抵抗率が減少(α < 0)します。これは「負の温度係数」と呼ばれます。
| 材料 | 温度特性 | 応用例 |
|---|---|---|
| シリコン(Si) | 温度↑で抵抗↓ | 温度センサー |
| ゲルマニウム(Ge) | 温度↑で抵抗↓ | サーミスタ |
💡 理由: 温度上昇でキャリア(電子・正孔)が増加し、電流が流れやすくなるため。
📊 温度による抵抗変化の計算例
【例題】銅線の温度による抵抗変化
【条件】
• 基準温度T₀ = 20℃での抵抗 R₀ = 10Ω
• 銅の温度係数 α = 0.00393 /℃
• 使用温度T = 100℃
【解答】
ΔT = 100 - 20 = 80℃
R = R₀(1 + αΔT)
R = 10 × (1 + 0.00393 × 80)
R = 10 × (1 + 0.3144)
R = 10 × 1.3144
➡ 温度が80℃上昇すると、抵抗は約31%増加!
🔗 関連記事:
📖 電験三種「理論」科目│温度と抵抗の計算問題
📖 電験三種の重要公式集
📖 YouTube動画で学ぶ電験三種
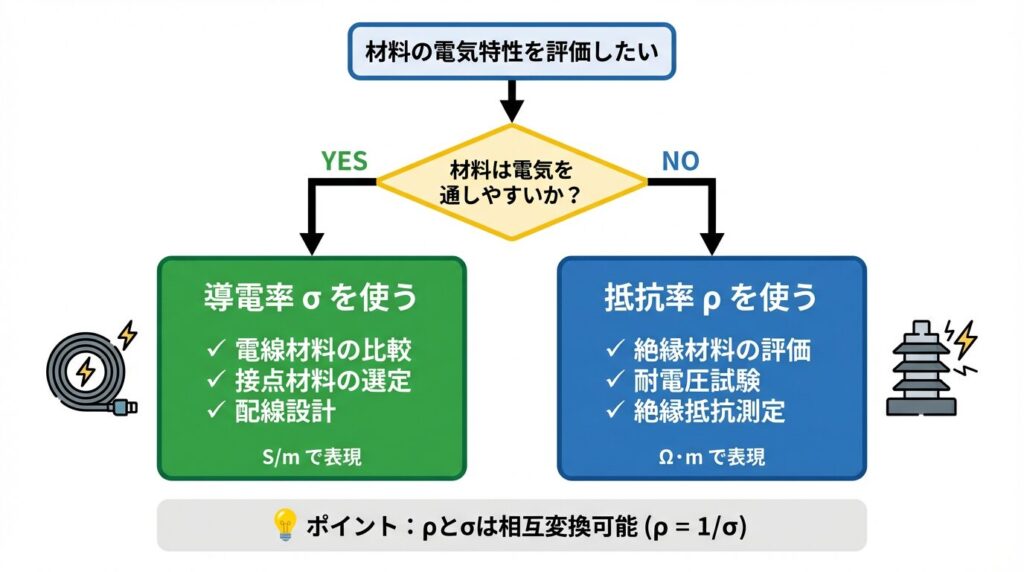
5️⃣ 実務でのρとσの使い分け
🧭 どちらを使うべきか?判断基準
基本的な判断ルール:
✅ 抵抗率ρを使う場面
• 絶縁材料の性能評価(値が大きいほど良い)
• 絶縁抵抗測定
• 耐電圧試験
• 「電気を通しにくさ」を強調したいとき
✅ 導電率σを使う場面
• 導電材料の性能評価(値が大きいほど良い)
• 電線・ケーブルの材料選定
• 接点材料の比較
• 「電気の通しやすさ」を強調したいとき
💼 具体的な実務例
【ケース1】電線材料の選定
目的: 電力損失の少ない電線を選びたい
使用指標: 導電率σ(大きいほど良い)
比較例:
• 銅: σ = 5.95 × 10⁷ S/m ← 優秀!
• アルミ: σ = 3.55 × 10⁷ S/m ← コスト重視なら選択肢
結論: 導電率で比較すると、銅のほうが約1.7倍電気を通しやすい!
【ケース2】絶縁材料の評価
目的: 高電圧機器の絶縁材料を選びたい
使用指標: 抵抗率ρ(大きいほど良い)
比較例:
• ガラス: ρ = 10¹⁰ ~ 10¹⁴ Ω・m ← 一般用途OK
• テフロン: ρ = 10²⁴ Ω・m ← 超高性能!
結論: 抵抗率で比較すると、テフロンは圧倒的に高性能!
【ケース3】電験三種の問題
問題文のヒント:
• 「電線の抵抗を求めよ」→ 抵抗率ρを使う
• 「導体の性能を比較せよ」→ 導電率σのほうが直感的
• 「絶縁材料の評価」→ 抵抗率ρを使う
💡 どちらが与えられていても、σ = 1/ρで変換可能!
📝 電験三種でよく出る計算パターン
【頻出パターン】導体の抵抗計算
【問題】
長さL = 100m、断面積A = 10mm²の銅線の抵抗を求めよ。
ただし、銅の抵抗率ρ = 1.7 × 10⁻⁸ Ω・mとする。
【解答】
まず単位を揃える:
• L = 100m
• A = 10mm² = 10 × 10⁻⁶ m² = 1.0 × 10⁻⁵ m²
抵抗の公式を使う:
R = ρL / A
R = (1.7 × 10⁻⁸) × 100 / (1.0 × 10⁻⁵)
R = 1.7 × 10⁻⁶ / 1.0 × 10⁻⁵
🔗 関連記事:
📖 電験三種「理論」科目の頻出計算問題
📖 電験三種で使える公式暗記術
📖 電験三種の合格率と難易度
📚 まとめ│ρとσを二度と混同しないために
🎯 この記事の重要ポイント
- 抵抗率ρは「電気の流れにくさ」を表し、単位はΩ・m
- 導電率σは「電気の流れやすさ」を表し、単位はS/m
- ρとσは逆数の関係(σ = 1/ρ)
- 絶縁材料の評価にはρ、導電材料の評価にはσを使う
- 金属は温度上昇で抵抗増加(α>0)、半導体は抵抗減少(α<0)
- 銅の抵抗率は約1.7×10⁻⁸ Ω・m(電験頻出!)
💪 次のステップ
初心者のあなたへ:
まずは「ρとσは逆数の関係」と「銅の抵抗率1.7×10⁻⁸ Ω・m」を覚えましょう。これだけで電験三種の問題の半分は解けます!
電験三種受験者のあなたへ:
過去問で「R = ρL/A」と「R = R₀(1+αΔT)」の計算問題を5問ずつ解いてみましょう。手を動かせば完璧です!
🔗 あわせて読みたい関連記事
📖 電験三種「理論」科目の完全攻略ガイド
📖 独学者のための電験三種試験対策
📖 電験三種の公式暗記術
📖 電験三種とは?資格の全体像を解説
📖 30代未経験から電験三種で年収500万円を目指す方法
📖 統計学の基礎│品質管理への応用