💡 こんな悩みはありませんか?
✅「二元配置実験の計算、どこから手をつければいいの?」
✅「交互作用の平方和って、なぜあんな計算式になるの?」
✅「分散分析表の数字が何を意味しているのか、イメージできない…」
🎯 この記事を読むとわかること
✔ 二元配置実験の計算を「0から完成まで」手を動かして学べる
✔ 交互作用の計算式の「なぜ」が直感的に理解できる
✔ 分散分析表の各項目(因子A・因子B・交互作用・誤差)を自分で計算できる
✔ F検定で「どの効果が有意か」を判定する方法
目次
🌟 はじめに:二元配置実験とは?
二元配置実験(Two-way ANOVA)とは、2つの因子を同時に調べ、それぞれの主効果と交互作用を分析する実験です。
【具体例】製品の強度を高めたい
🌡️ 因子A:加熱温度(低温/高温)
⏱️ 因子B:加熱時間(短時間/長時間)
❓ 疑問:「温度と時間の組み合わせで、ベストな条件は?」「温度と時間に相性(交互作用)はある?」
一元配置実験では1つの因子しか調べられませんが、二元配置実験なら2因子の相乗効果(交互作用)も分析できます。
この記事では、実際のデータを使って、二元配置実験の分散分析表を1から完成させる全手順を解説します!
📋 今回使う実験データ
実験の設定
実験データ(引張強度)
| 温度\時間 | B1(短時間) | B2(長時間) | 行合計 | ||||
|---|---|---|---|---|---|---|---|
| 1回目 | 2回目 | 小計 | 1回目 | 2回目 | 小計 | ||
| A1(低温) | 45 | 47 | 92 | 52 | 54 | 106 | 198 |
| A2(高温) | 50 | 48 | 98 | 46 | 44 | 90 | 188 |
| 列合計 | — | 190 | — | 196 | 386 | ||
📊 データの読み方
🔹 セル(A1, B1):低温×短時間の組み合わせ → 45, 47(平均46.0)
🔹 セル(A1, B2):低温×長時間の組み合わせ → 52, 54(平均53.0)
🔹 総データ数:N = 2水準 × 2水準 × 2回 = 8
📊 【STEP 0】分散分析の全体像を理解する
データのばらつきを4つに分解する
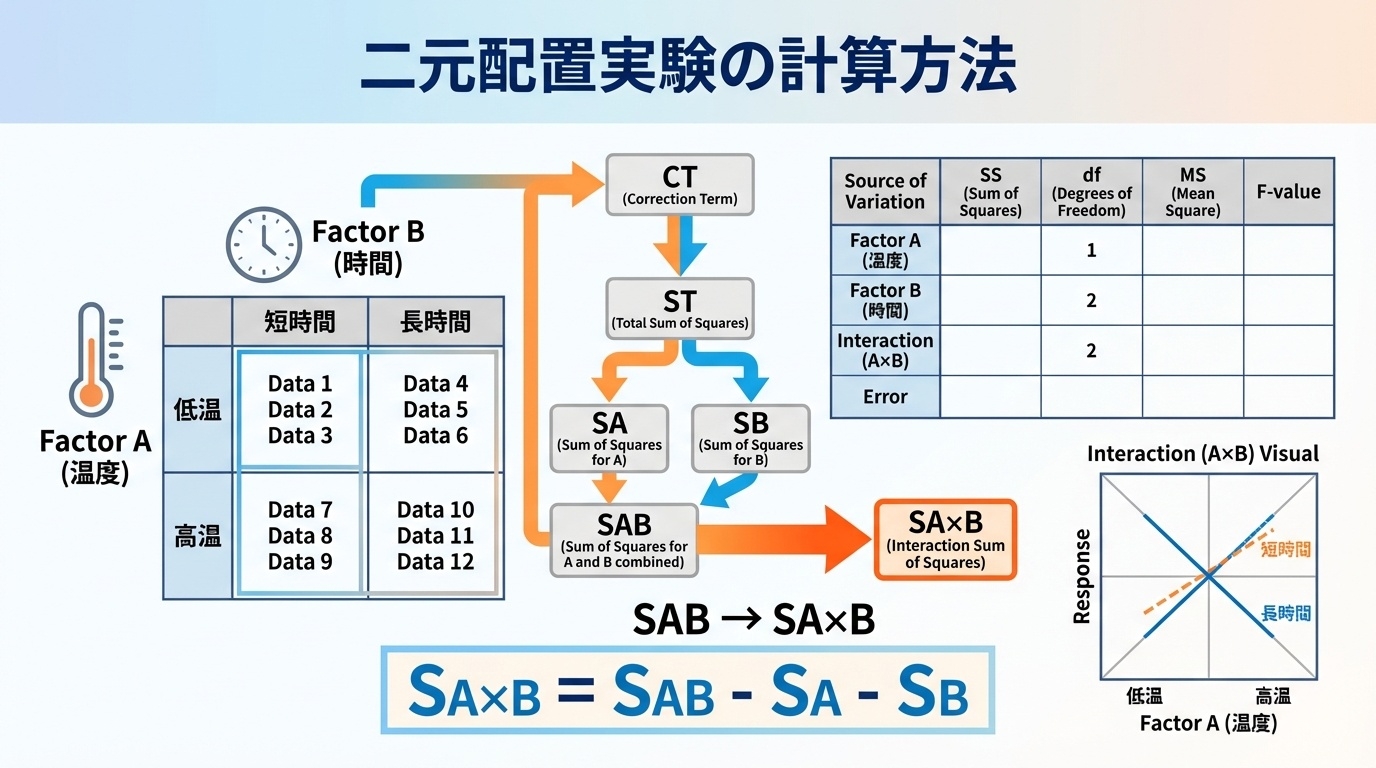
二元配置実験では、総平方和(ST)を4種類のばらつきに分解します。
📐 平方和の分解式
ST = SA + SB + SA×B + Se
🔹 SA:因子A(温度)の効果
🔹 SB:因子B(時間)の効果
🔹 SA×B:交互作用(温度と時間の相性)
🔹 Se:誤差(偶然のばらつき)
分散分析表の完成形(ゴール)
| 要因 | 平方和(S) | 自由度(φ) | 平均平方(V) | F値 |
|---|---|---|---|---|
| 因子A(温度) | ? | ? | ? | ? |
| 因子B(時間) | ? | ? | ? | ? |
| 交互作用(A×B) | ? | ? | ? | ? |
| 誤差(e) | ? | ? | ? | — |
| 総計(T) | ? | ? | — | — |
👉 交互作用とは?で交互作用の基礎を理解しておくと、この先の計算がスムーズです。
🔢 【STEP 1】修正項(CT)の計算
修正項(CT)は、一元配置と同じように計算します。
📐 修正項の計算式
CT = T² / N
🔢 計算
総和(T)= 386、データ数(N)= 8
CT = 386² / 8 = 148,996 / 8
CT = 18,624.5
🔢 【STEP 2】総平方和(ST)の計算
📐 総平方和の計算式
ST = Σ(各データ²) - CT
🔢 計算
45² + 47² + 52² + 54² + 50² + 48² + 46² + 44² = 18,710
ST = 18,710 - 18,624.5
ST = 85.5
🔢 【STEP 3】因子Aの平方和(SA)の計算
因子Aの平方和とは?
因子A(温度)の平方和は、「温度を変えた効果」によるばらつきを表します。
📐 因子Aの平方和の計算式
SA = Σ(各A水準の合計² / その水準のデータ数) - CT
💡 ポイント:A1とA2の「行合計」を使います
🔢 計算
A1(低温)の行合計:198(データ数4個)
A2(高温)の行合計:188(データ数4個)
SA = (198² / 4) + (188² / 4) - CT
SA = (39,204 / 4) + (35,344 / 4) - 18,624.5
SA = 9,801 + 8,836 - 18,624.5
SA = 18,637 - 18,624.5
SA = 12.5
🔢 【STEP 4】因子Bの平方和(SB)の計算
因子Bの平方和とは?
因子B(時間)の平方和は、「時間を変えた効果」によるばらつきを表します。
📐 因子Bの平方和の計算式
SB = Σ(各B水準の合計² / その水準のデータ数) - CT
💡 ポイント:B1とB2の「列合計」を使います
🔢 計算
B1(短時間)の列合計:190(データ数4個)
B2(長時間)の列合計:196(データ数4個)
SB = (190² / 4) + (196² / 4) - CT
SB = (36,100 / 4) + (38,416 / 4) - 18,624.5
SB = 9,025 + 9,604 - 18,624.5
SB = 18,629 - 18,624.5
SB = 4.5
🔥 【STEP 5】交互作用の平方和(SA×B)の計算 ← 最重要!
交互作用とは何か?
交互作用とは、「AとBの組み合わせによって生じる追加効果」です。
🔥 交互作用の具体例
もし交互作用がなければ:
・低温で+5の効果、長時間で+7の効果
・低温×長時間なら +5+7=+12 のはず
しかし実際には:
・低温×長時間で +15 の効果(+3の追加効果!)
→ この「+3」が交互作用です
なぜこの計算式になるのか?
交互作用の平方和は、「セル(組み合わせ)のばらつき」から「AとBの単独効果」を引いたものです。
📐 交互作用の平方和の計算式
SA×B = SAB - SA - SB
まずSAB(セルの平方和)を計算します:
SAB = Σ(各セルの合計² / 繰り返し数) - CT
💡 なぜこの式で交互作用が求まるのか?
【考え方】
1. SAB:全ての組み合わせ効果(A+B+交互作用)
2. SA:Aの単独効果
3. SB:Bの単独効果
SABから「SA」と「SB」を引けば、「組み合わせによる追加効果」だけが残るのです!
STEP 5-1: セルの平方和(SAB)を計算
📊 各セル(組み合わせ)の合計
セル(A1, B1):92(繰り返し2回)
セル(A1, B2):106(繰り返し2回)
セル(A2, B1):98(繰り返し2回)
セル(A2, B2):90(繰り返し2回)
🔢 SABの計算
SAB = (92² / 2) + (106² / 2) + (98² / 2) + (90² / 2) - CT
SAB = (8,464 / 2) + (11,236 / 2) + (9,604 / 2) + (8,100 / 2) - 18,624.5
SAB = 4,232 + 5,618 + 4,802 + 4,050 - 18,624.5
SAB = 18,702 - 18,624.5
SAB = 77.5
STEP 5-2: 交互作用の平方和を計算
🔢 交互作用の計算
SA×B = SAB - SA - SB
SA×B = 77.5 - 12.5 - 4.5
SA×B = 60.5
🔥 この結果の意味
交互作用の平方和(60.5)が非常に大きい!
→ 温度と時間の「組み合わせ効果」が強いことを示しています。
→ 「温度だけ」「時間だけ」で考えるのではなく、「どの組み合わせが最適か」を見極める必要があります。
👉 交互作用の詳しい解説で、グラフを使った理解を深めましょう。
🔢 【STEP 6】誤差の平方和(Se)の計算
誤差の平方和とは?
誤差(Se)は、偶然のばらつき(測定誤差など)を表します。
📐 誤差の平方和の計算式
Se = ST - SA - SB - SA×B
(引き算で簡単に求まります!)
🔢 誤差の計算
Se = ST - SA - SB - SA×B
Se = 85.5 - 12.5 - 4.5 - 60.5
Se = 8.0
🔢 【STEP 7】自由度の計算
自由度は、各要因の「自由に決められる数の個数」です。
📐 自由度の計算式
総自由度:φT = N - 1 = 8 - 1 = 7
因子Aの自由度:φA = a - 1 = 2 - 1 = 1
因子Bの自由度:φB = b - 1 = 2 - 1 = 1
交互作用の自由度:φA×B = (a-1) × (b-1) = 1 × 1 = 1
誤差の自由度:φe = ab(r-1) = 2×2×(2-1) = 4
✅ 確認
φT = φA + φB + φA×B + φe
7 = 1 + 1 + 1 + 4 ✅ 正しい!
🔢 【STEP 8】平均平方(V)とF値の計算
平均平方の計算
📐 平均平方の計算式
V = S / φ(平方和 ÷ 自由度)
🔢 各平均平方の計算
VA:12.5 / 1 = 12.5
VB:4.5 / 1 = 4.5
VA×B:60.5 / 1 = 60.5
Ve:8.0 / 4 = 2.0
F値の計算
📐 F値の計算式
F = V(要因) / Ve(誤差)
🔢 各F値の計算
FA:12.5 / 2.0 = 6.25
FB:4.5 / 2.0 = 2.25
FA×B:60.5 / 2.0 = 30.25
📊 分散分析表の完成!
| 要因 | 平方和(S) | 自由度(φ) | 平均平方(V) | F値 |
|---|---|---|---|---|
| 因子A(温度) | 12.5 | 1 | 12.5 | 6.25 |
| 因子B(時間) | 4.5 | 1 | 4.5 | 2.25 |
| 交互作用(A×B) | 60.5 | 1 | 60.5 | 30.25 |
| 誤差(e) | 8.0 | 4 | 2.0 | — |
| 総計(T) | 85.5 | 7 | — | — |
🎉 分散分析表が完成しました!
次は、このF値を使って「統計的に有意かどうか」を判定します。
🔍 【STEP 9】F検定による判定
F分布表で臨界値を確認
有意水準5%のF分布表から臨界値を確認します。
| 要因 | 自由度 | F値 | F0.05の臨界値 | 判定 |
|---|---|---|---|---|
| 因子A | (1, 4) | 6.25 | 7.71 | 有意でない |
| 因子B | (1, 4) | 2.25 | 7.71 | 有意でない |
| 交互作用 | (1, 4) | 30.25 | 7.71 | 有意! |
✅ 判定結果
❌ 因子A(温度):単独では有意でない(6.25 < 7.71)
❌ 因子B(時間):単独では有意でない(2.25 < 7.71)
✅ 交互作用(A×B):有意差あり!(30.25 > 7.71)
結果の解釈
🔥 この結果が意味すること
✅ 温度だけで強度を高めることはできない
✅ 時間だけで強度を高めることもできない
✅ しかし「温度と時間の組み合わせ」が重要!
→ 最適な組み合わせを見つけることが鍵です
最適条件の決定
| 組み合わせ | 平均強度 |
|---|---|
| 低温×短時間 | 46.0 |
| 低温×長時間 | 53.0 ⭐ |
| 高温×短時間 | 49.0 |
| 高温×長時間 | 45.0 |
✅ 結論
最適条件:低温×長時間(平均強度53.0)
この組み合わせで製品の引張強度を最大化できます。
👉 F検定の判定方法で、F分布表の使い方を詳しく学べます。
📝 まとめ
✅ この記事のポイント
🔹 二元配置実験では、2つの因子とその交互作用を同時に分析できる
🔹 交互作用の計算は「SAB - SA - SB」で、組み合わせの追加効果を表す
🔹 交互作用が有意なら、因子の組み合わせを重視すべき
🔹 F検定で各効果の統計的有意性を判定できる
🎓 さらに学びを深めるには
📌 二元配置実験とは?で概念を復習
📌 交互作用とは?グラフが交差する本当の意味で視覚的に理解
📌 一元配置実験の計算方法で基礎を固める
📌 分散分析表の作り方完全ガイドで理論を深める
📌 実験計画法の学習マップで体系的に学習
🚀 次の記事へ
📖 次はこちらの記事がおすすめ!
二元配置実験の計算をマスターした次は、「さらに多くの因子を効率的に調べる方法」を学びましょう。
👉 次の記事:直交配列表とは?実験回数を劇的に削減する方法
🔹 直交配列表を理解すると、3つ以上の因子でも少ない試行回数で実験できるようになります!
📚 実験計画法の「挫折」を救う2冊
「数式を見た瞬間に本を閉じた」
そんな経験がある私だからこそ推せる、厳選のバイブルです。