- 乱塊法の分散分析表は作れるけど、その後の計算がわからない
- 通常の二元配置実験と何が違うの?ブロック因子ってどう扱えばいい?
- 「差の点推定値」「差の信頼区間」って何?なぜ「差」を使うの?
- ブロック因子の母分散σ²ᵣの求め方が意味不明…
- E(Vᵣ)の式が出てきたけど、なぜこの形になるのかわからない
- 乱塊法と通常の二元配置実験の「決定的な違い」
- ブロック因子がある場合の最適水準の選び方
- なぜ「差」の推定を行うのか、その理由と計算方法
- ブロック因子の母分散σ²ᵣを推定する公式の意味と導出
乱塊法(Randomized Block Design)は、実験計画法の中でも実務で非常によく使われる手法です。
例えば「2日間に分けて実験する」「3台の機械で実験する」「4人の作業者で実験する」など、実験環境に避けられないばらつきがある場合に使います。
分散分析表を作るところまでは、通常の二元配置実験や三元配置実験と同じ手順なので、比較的スムーズにできる方が多いです。
しかし、その後の「最適水準の選び方」「点推定」「信頼区間」「ブロック分散の推定」になると、急に難しく感じる方が多いのではないでしょうか。
この記事では、乱塊法特有の考え方を「なぜそうするのか」から丁寧に解説していきます。
目次
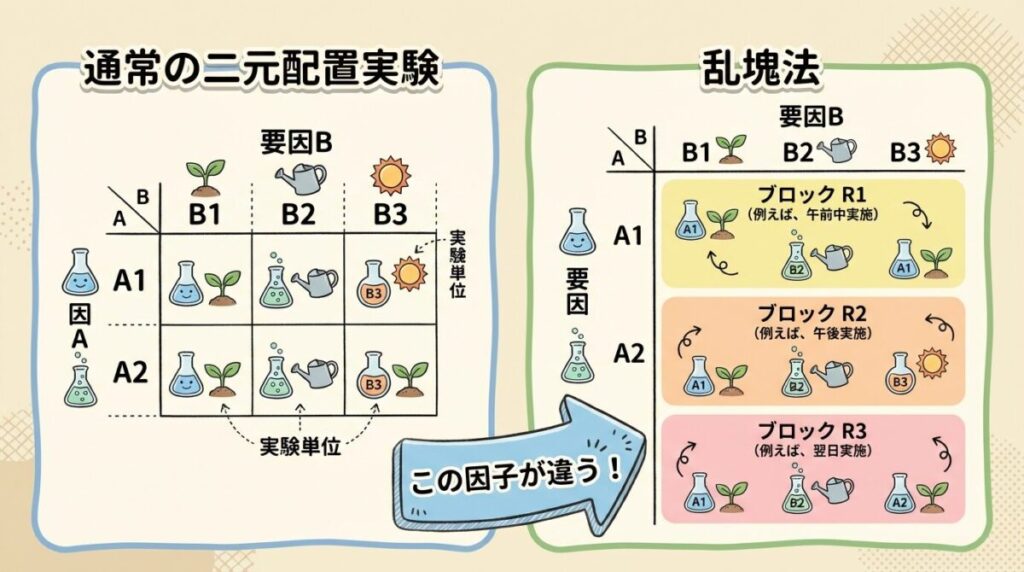
乱塊法と通常の二元配置実験の「決定的な違い」
まず、乱塊法が通常の実験計画とどう違うのかを明確にしましょう。この違いを理解しないと、後の計算の意味がわかりません。
通常の二元配置実験
因子A:温度(A₁=100℃、A₂=120℃)← 調べたい因子
因子B:時間(B₁=10分、B₂=20分、B₃=30分)← 調べたい因子
→ AもBも「どの水準が最適か知りたい」因子
乱塊法(ブロック因子がある場合)
因子A:温度(A₁=100℃、A₂=120℃)← 調べたい因子
因子B:時間(B₁=10分、B₂=20分、B₃=30分)← 調べたい因子
因子R(ブロック因子):実験日(R₁=1日目、R₂=2日目)← 調べたくないけど影響がある因子
→ Rは「環境ノイズを吸収するため」に入れた因子。最適水準を選ぶ対象ではない!
ブロック因子とは何か?
ブロック因子を理解するために、具体例で考えてみましょう。
あなたはパンケーキの最適なレシピを調べる実験をしています。
- 因子A(調べたい):砂糖の量(A₁=少なめ、A₂=多め)
- 因子B(調べたい):焼き時間(B₁=2分、B₂=3分、B₃=4分)
しかし、1日で全ての実験ができないので、2日間に分けて実験することになりました。
問題:1日目と2日目で「室温」「湿度」「フライパンの状態」などが微妙に違う可能性がある!
解決策:「実験日」をブロック因子Rとして分析に組み込む。こうすることで、日によるばらつきを「誤差」から分離できる。
ブロック因子は「興味はないけど、影響がある因子」です。
- 「R₁(1日目)とR₂(2日目)のどちらが良いか」には興味がない
- でも、日によるばらつきが結果に影響するのは事実
- だから、その影響を分離して取り除くためにブロック因子として扱う
乱塊法とは?実験条件にばらつきがあるときの設計法 →
【例題】乱塊法の実験データ
ここからは、具体的な例題を使って乱塊法の分析手順を解説していきます。
製品の強度を調べる実験を行った。
- 因子A(材料):2水準(A₁、A₂)
- 因子B(加工法):3水準(B₁、B₂、B₃)
- 因子R(ブロック:実験日):2水準(R₁=1日目、R₂=2日目)
- 目的:強度を最大にしたい(望大特性)
- 現行条件:A₁B₁
1日に最大6回しか実験できないため、2日間に分けて計12回の実験を行った。
実験データ(表1)
| 因子B(加工法) | ||||
|---|---|---|---|---|
| B₁ | B₂ | B₃ | ||
| R₁ (1日目) |
A₁ | 18 | 24 | 22 |
| A₂ | 25 | 32 | 35 | |
| R₂ (2日目) |
A₁ | 22 | 28 | 26 |
| A₂ | 28 | 36 | 40 | |
計算補助表(各水準の合計値)
ブロック因子R
| R₁ | 156 |
| R₂ | 180 |
因子A × 因子B
| B₁ | B₂ | B₃ | 合計 | |
| A₁ | 40 | 52 | 48 | 140 |
| A₂ | 53 | 68 | 75 | 196 |
| 合計 | 93 | 120 | 123 | 336 |
分散分析表(既に完成しているとする)
| 要因 | 平方和 S | 自由度 φ | 分散 V | F₀ | 判定 |
|---|---|---|---|---|---|
| R | 48.0 | 1 | 48.0 | 24.0 | 有意 ** |
| A | 261.3 | 1 | 261.3 | 130.7 | 有意 ** |
| B | 90.5 | 2 | 45.3 | 22.6 | 有意 ** |
| A×B | 12.2 | 2 | 6.1 | 3.05 | 有意 * |
| E(誤差) | 10.0 | 5 | 2.0 | − | − |
| T(総計) | 422.0 | 11 | − | − | − |
- ブロック因子R(日間変動):有意 → 日によるばらつきがある
- 因子A(材料):有意
- 因子B(加工法):有意
- 交互作用A×B:有意 → AとBは組み合わせで考える必要あり
【Step 1】最適水準の選び方|ブロック因子は無視する!
分散分析の結果、交互作用A×Bが有意でした。では、最適水準はどう選べばよいでしょうか?
乱塊法での最適水準選択ルール
【ルール1】ブロック因子Rは最適水準の選択に使わない
→ R₁とR₂のどちらが良いかは考えない。将来の実験がどの「日」に行われるかはコントロールできないから。
【ルール2】AとBについては通常どおり
- 交互作用A×Bが有意 → 組み合わせで選ぶ
- 交互作用A×Bが有意でない → 単独で選ぶ
この例題での最適水準
交互作用A×Bが有意なので、AとBの「組み合わせ」で最適水準を選びます。
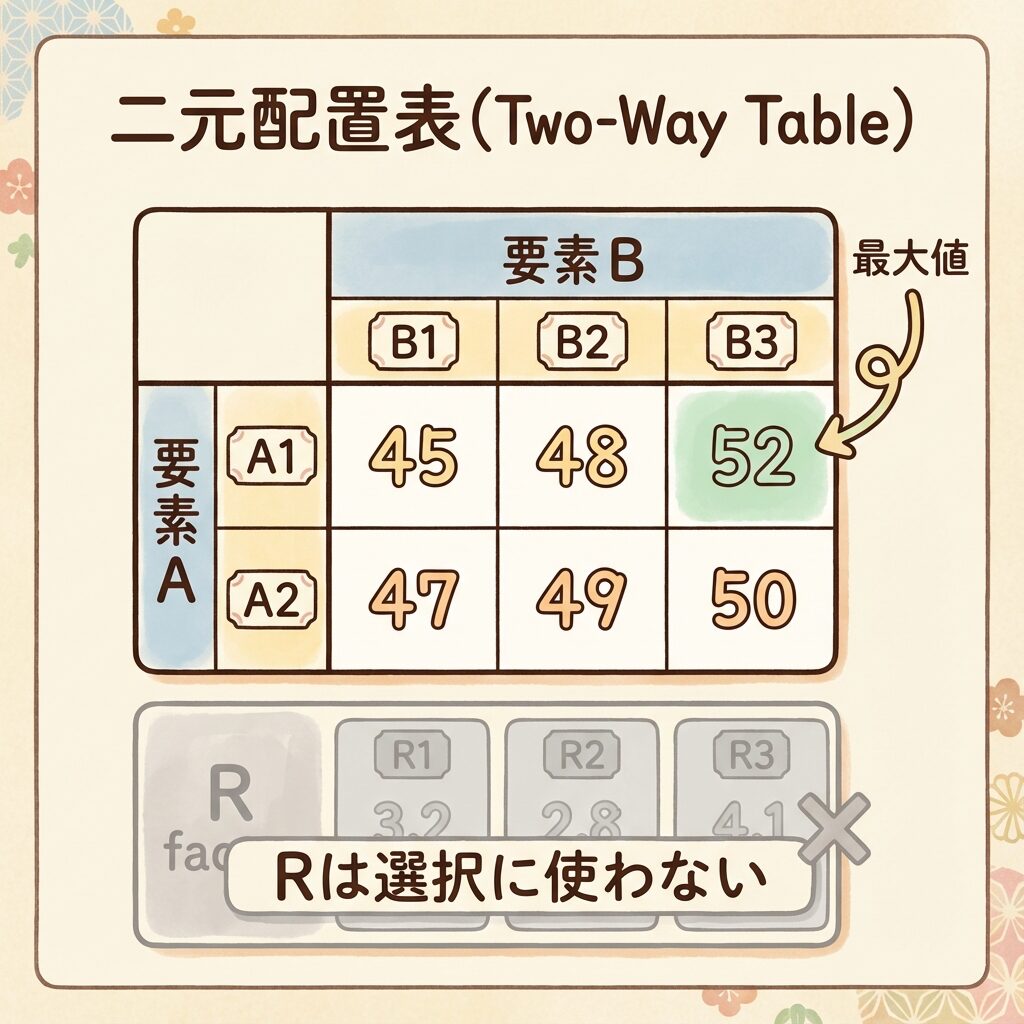
計算補助表のA×Bの部分を見て、最大値を探します:
| B₁ | B₂ | B₃ | |
| A₁ | 40 | 52 | 48 |
| A₂ | 53 | 68 | 75 ← 最大! |
最適水準は「A₂B₃」
※ブロック因子R(実験日)については言及しない
ブロック因子は「制御できない環境要因」だからです。
「R₂(2日目)の方が結果が良かったから、今後はR₂で実験しよう」とは言えませんよね。将来の実験がどんな日(天気、湿度、作業者の調子など)に行われるかは、事前にコントロールできません。
だから、AとBの組み合わせだけを最適化し、Rの影響は「平均的に」考えるのです。
【Step 2】なぜ「差」の推定を行うのか?|乱塊法の核心
ここが乱塊法で最も重要かつ多くの人が混乱するポイントです。
通常の実験計画法では「最適水準での母平均μ̂」を点推定しますが、乱塊法では「最適水準と現行条件の差」を推定することが多いです。
なぜでしょうか?
理由:「差」を取るとブロック効果が消える
これを理解するために、まず「単独の点推定」をした場合の問題点を見てみましょう。
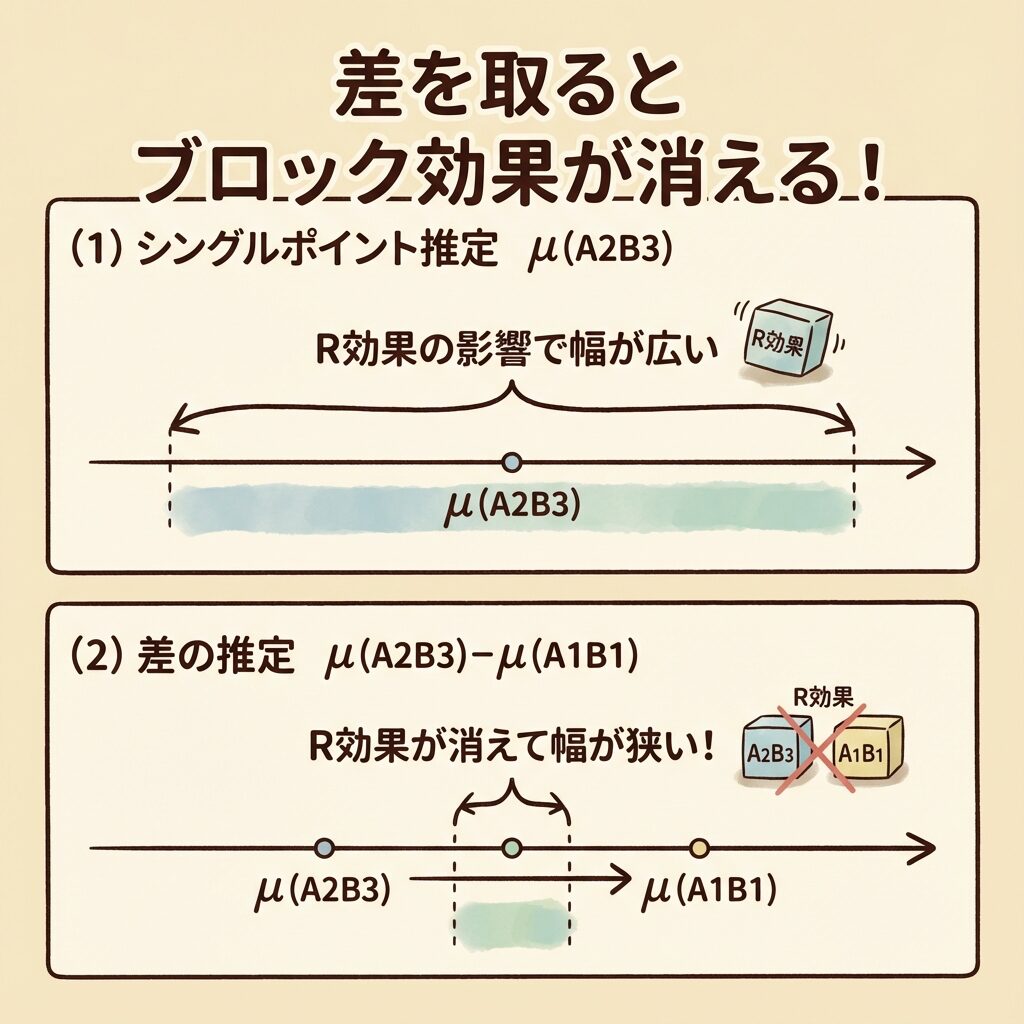
問題:単独の点推定だと区間が広くなる
もし「A₂B₃での母平均」を単独で推定しようとすると、その信頼区間にはブロック因子Rの不確実性も含まれてしまいます。
A₂B₃のデータは「R₁での35」と「R₂での40」の2つ。
→ この5の差には、「A₂B₃の真の効果」+「日によるばらつき(R効果)」が混ざっている
→ 信頼区間を計算すると、Rの効果の分だけ幅が広くなってしまう
解決策:「差」を取るとR効果が相殺される
ここで「最適水準A₂B₃」と「現行条件A₁B₁」の差を考えてみましょう。
R₁(1日目)での差:
A₂B₃の値 − A₁B₁の値 = 35 − 18 = 17
R₂(2日目)での差:
A₂B₃の値 − A₁B₁の値 = 40 − 22 = 18
→ どちらの日でも、差はほぼ同じ(17〜18)になっている!
これはなぜでしょうか?
R₁(1日目)はすべての実験に「+0」の影響を与え、
R₂(2日目)はすべての実験に「+4」の影響を与えたとします(分散分析でRが有意だったので)。
R₁での差:
(A₂B₃の真の値 + 0) − (A₁B₁の真の値 + 0) = A₂B₃の真の値 − A₁B₁の真の値
R₂での差:
(A₂B₃の真の値 + 4) − (A₁B₁の真の値 + 4) = A₂B₃の真の値 − A₁B₁の真の値
→ どちらも同じ!Rの効果(+0や+4)が相殺されて消えるのです。
この性質を利用して、乱塊法では「差」の点推定と信頼区間を求めるのです。
【Step 3】差の点推定値の計算
では、実際に「最適水準A₂B₃と現行条件A₁B₁の差」の点推定値を計算してみましょう。
差の点推定値の公式
x̄₂₃.:A₂B₃のデータの平均(Rは全水準をまとめて平均)
x̄₁₁.:A₁B₁のデータの平均(Rは全水準をまとめて平均)
計算例
Step 1:各組み合わせの平均を求める
A₂B₃の合計 = 75(計算補助表より)
A₂B₃のデータ数 = 2(R₁とR₂の2回)
x̄₂₃. = 75 / 2 = 37.5
A₁B₁の合計 = 40(計算補助表より)
A₁B₁のデータ数 = 2(R₁とR₂の2回)
x̄₁₁. = 40 / 2 = 20.0
Step 2:差を計算する
差の点推定値 = x̄₂₃. − x̄₁₁. = 37.5 − 20.0 = 17.5
最適水準A₂B₃は、現行条件A₁B₁よりも強度が平均17.5高くなると推定されます。
この計算ではブロック因子Rの効果を使っていません。
A₂B₃の平均もA₁B₁の平均も、R₁とR₂の両方のデータを含んでいるので、差を取ると自然にRの効果が相殺されます。
【Step 4】差の信頼区間の計算|ここが乱塊法のヤマ場
差の点推定値が求まったら、次は信頼区間を計算します。これが乱塊法で最も出題されやすい計算です。
差の信頼区間の公式
VE:誤差分散(分散分析表から)
r:ブロック因子Rの水準数
φE:誤差の自由度
t(φE, 0.05):t分布の上側2.5%点
なぜこの公式になるのか?(導出の解説)
この公式を丸暗記するのではなく、なぜこの形になるのかを理解しましょう。
ポイント1:差の分散は「和」になる
2つの独立な確率変数の差の分散は、それぞれの分散の和になります。
V(x̄₂₃. − x̄₁₁.) = V(x̄₂₃.) + V(x̄₁₁.)
ポイント2:各平均の分散はVE/rで近似
x̄₂₃.(A₂B₃の平均)は、r個のデータ(ブロック数分)の平均なので:
V(x̄₂₃.) = VE / r
V(x̄₁₁.) = VE / r
ポイント3:合わせると2VE/r
V(x̄₂₃. − x̄₁₁.) = VE/r + VE/r = 2VE/r
この平方根を取ったものが、信頼区間の「幅」の計算に使われるのです。
2VE/rの「2」は、2つの平均の差を取っているから。
r(ブロック数)で割るのは、各平均がr個のデータから計算されているから。
分散と標準偏差|「バラつき」を数値化する魔法の公式 →
計算例:信頼区間を求める
- 差の点推定値:17.5
- 誤差分散 VE = 2.0(分散分析表から)
- 誤差の自由度 φE = 5
- ブロック因子Rの水準数 r = 2
- t(5, 0.05) = 2.571
Step 1:差の標準誤差を計算
差の分散 = 2VE / r = 2 × 2.0 / 2 = 2.0
差の標準誤差 = √2.0 = 1.414
Step 2:信頼区間の幅を計算
幅 = t(5, 0.05) × √(2VE/r)
= 2.571 × 1.414
= 3.64
Step 3:95%信頼区間を計算
下限 = 17.5 − 3.64 = 13.86
上限 = 17.5 + 3.64 = 21.14
最適水準A₂B₃と現行条件A₁B₁の強度の差は、95%の信頼度で
13.86 ≦ μ(A₂B₃) − μ(A₁B₁) ≦ 21.14
の範囲にあると推定されます。
信頼下限は13.86(信頼下限 = 点推定値 − 幅 = 17.5 − 3.64)
信頼下限が正(13.86 > 0)なので、「A₂B₃がA₁B₁より確実に良い」と言えます。
もし信頼区間が0をまたいでいたら(例:−2 〜 +15)、「本当に良いかどうかは断言できない」となります。
【Step 5】ブロック因子の母分散σ²ᵣの推定|なぜこの公式?
乱塊法では、もう一つ重要な計算があります。それは「ブロック因子Rの母分散σ²ᵣ」の推定です。
これは「日によるばらつきがどれくらいあるのか」を数値化するものです。
ブロック分散の推定公式
VR:ブロック因子Rの分散(分散分析表から)
VE:誤差分散(分散分析表から)
a:因子Aの水準数
b:因子Bの水準数
なぜこの公式になるのか?(導出の解説)
この公式を理解するために、平均平方の期待値E(V)という概念を使います。
平均平方の期待値とは?
分散分析表で計算する「分散V」は、「真の分散σ²」の推定値です。
「Vを何度も計算したときの平均値」が期待値E(V)であり、これは真の分散σ²と関係しています。
誤差分散の期待値:
E(VE) = σ²E
ブロック因子Rの分散の期待値:
E(VR) = σ²E + (a × b) × σ²R
なぜE(VR)に「a × b」が掛かるのか?
これが最も理解しにくいポイントです。直感的に説明しましょう。
ブロック因子R(例:1日目 vs 2日目)の各水準には、a × b 個のデータが含まれています。
この例では:
・R₁(1日目)のデータ:A₁B₁, A₁B₂, A₁B₃, A₂B₁, A₂B₂, A₂B₃ → 6個(= 2 × 3)
・R₂(2日目)のデータ:A₁B₁, A₁B₂, A₁B₃, A₂B₁, A₂B₂, A₂B₃ → 6個(= 2 × 3)
R₁とR₂の「差」を計算するとき、この6個分のデータが使われます。
つまり、Rの効果は「6倍に増幅されて」VRに含まれているのです。
だから、σ²Rを取り出すには「a × b = 6」で割る必要があります。
公式の導出
E(VR) = σ²E + (a × b) × σ²R より:
(a × b) × σ²R = E(VR) − σ²E
σ²R = {E(VR) − σ²E} / (a × b)
実際の推定では、E(V)の代わりにVを使うので:
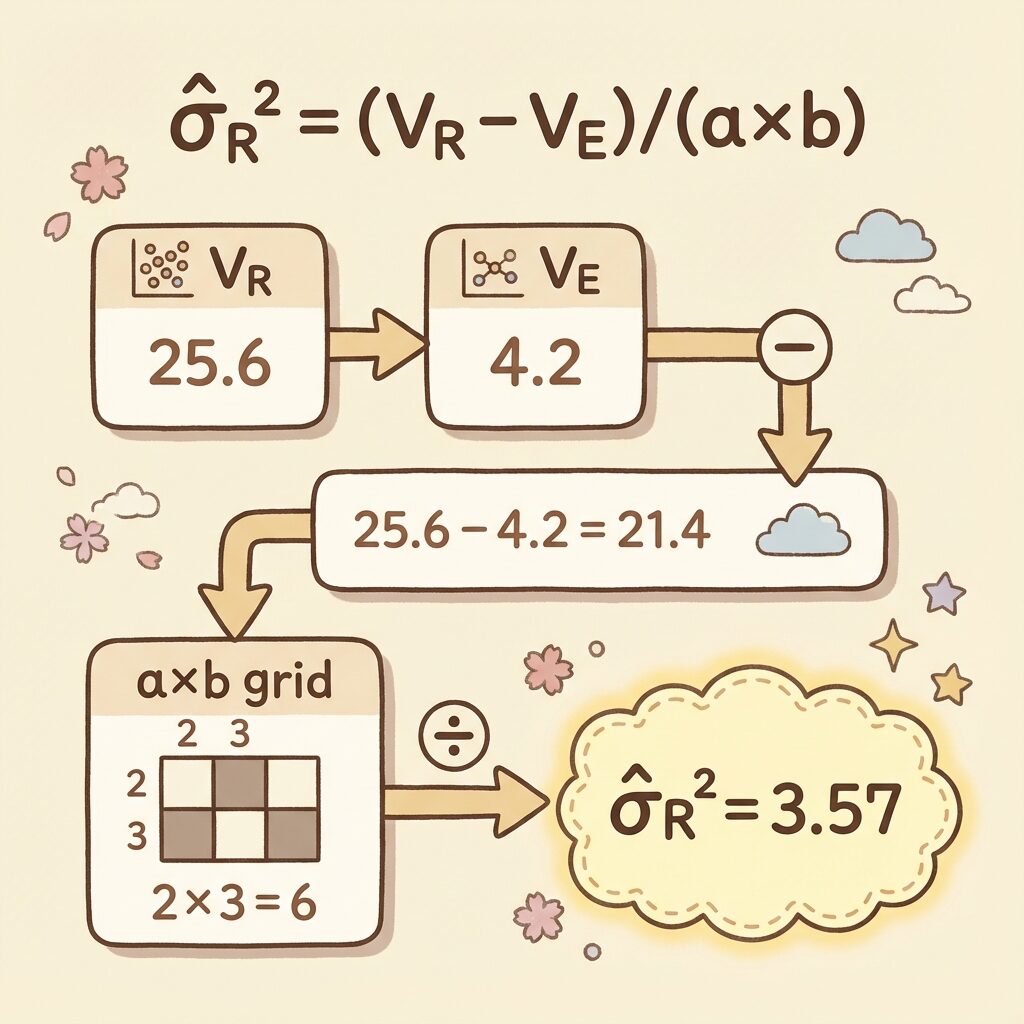
σ̂²R = (VR − VE) / (a × b)

計算例:ブロック分散σ̂²ᵣを求める
- VR = 48.0(分散分析表から)
- VE = 2.0(分散分析表から)
- 因子Aの水準数 a = 2
- 因子Bの水準数 b = 3
計算:
σ̂²R = (VR − VE) / (a × b)
= (48.0 − 2.0) / (2 × 3)
= 46.0 / 6
= 7.67
日間変動(ブロック因子R)の母分散は約7.67と推定されます。
これは「日によって、平均的に±√7.67 ≒ ±2.8程度のばらつきがある」ことを意味します。
この値が大きいほど、「日によるばらつきが大きい」ことを意味します。
もしσ̂²Rが誤差分散VEより大きければ、「日による影響を減らす対策」を検討する価値があります(例:空調管理、原料ロット管理など)。
【まとめ】乱塊法 vs 通常の二元配置実験 比較表
最後に、乱塊法と通常の二元配置実験の違いを一覧表でまとめます。
| 項目 | 通常の二元配置実験 | 乱塊法 |
|---|---|---|
| 因子の種類 | A, B(どちらも興味あり) | A, B(興味あり)+ R(ブロック因子) |
| 最適水準の選び方 | AとBから選ぶ | AとBから選ぶ(Rは無視) |
| 点推定の対象 | 最適水準の母平均 μ̂ | 差の推定(最適 − 現行)が有用 |
| 信頼区間の公式 | μ̂ ± t × √(VE/ne) | 差 ± t × √(2VE/r) |
| 追加で求めるもの | (特になし) | ブロック分散 σ̂²R |
| σ̂²Rの公式 | − | (VR − VE) / (a × b) |
計算のチェックリスト
ブロック因子Rも含めてF検定を行う
AとBのみで選ぶ(Rは無視)、交互作用の有意性に応じて組み合わせ or 単独
x̄(最適) − x̄(現行)
差 ± t × √(2VE/r)、rはブロック数
σ̂²R = (VR − VE) / (a × b)
【保存版】公式早見表
乱塊法の公式一覧
| 差の点推定値 | x̄(最適) − x̄(現行) |
| 差の分散 | 2VE / r (r = ブロック数) |
| 差の95%信頼区間 | 差 ± t(φE, 0.05) × √(2VE/r) |
| ブロック分散の推定 | σ̂²R = (VR − VE) / (a × b) |
| E(VR)の式 | E(VR) = σ²E + (a × b) × σ²R |
覚えておくべきポイント
- ブロック因子は最適水準の選択に使わない
- 「差」を取るとブロック効果が相殺される
- 差の分散の「2」は、2つの平均の差を取るから
- σ̂²Rの「a × b」は、各ブロックに含まれるデータ数
📚 次に読むべき記事
乱塊法の基本概念を復習したい方へ
E(V)の考え方をもっと深く理解したい方へ
実験計画法の全体像を把握したい方へ
交互作用の基本を復習したい方へ
乱塊法では、ブロック因子(日間変動など)を「興味のない環境要因」として扱います。最適水準の選択ではブロック因子を無視し、推定では「差」を取ることでブロック効果を相殺するのがポイントです。公式を丸暗記するのではなく、「なぜそうするのか」を理解することで、応用問題にも対応できるようになります。