「1つの因子だけでは物足りない...」
実際の現場では、複数の要因が同時に結果に影響することがほとんどです。
🍛 例えば「カレーの美味しさ」は、肉の種類だけでなくスパイスの量にも左右されます。
そんなときに活躍するのが「二元配置実験」!
2つの因子を同時に分析して、相乗効果(交互作用)まで明らかにできる最強の実験手法です!
📌 この記事で分かること
- 二元配置実験と一元配置実験の違いが一目瞭然
- 主効果と交互作用の概念を完全理解
- カレー評価データを使った具体的な計算手順(8ステップ)
- 分散分析表の読み方と結果の解釈方法
一元配置実験では、「1つの因子」だけを調べました。
しかし実際の現場では、複数の因子が同時に影響することが多いですよね。
「肉の種類を変えると味が変わる」のは分かった。
でも、「スパイスの量も同時に変えたら、どうなるんだろう?」
「もしかして、豚肉×スパイス多という組み合わせが特別に美味しいんじゃないか?」
💡 そんな「組み合わせの特別な効果」を調べられるのが、二元配置実験なのです!
目次
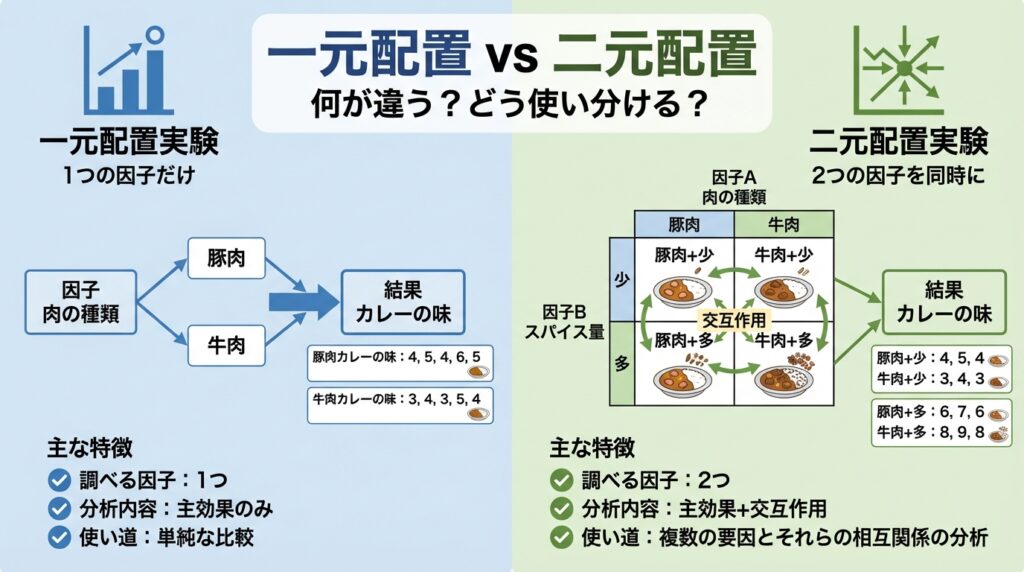
一元配置 vs 二元配置:何が違う?
まずは、一元配置実験と二元配置実験の違いを整理しましょう。
この違いを理解すれば、どちらを使うべきかすぐに判断できます!
💡 ポイント
- 一元配置は1つの因子の効果だけを調べる
- 二元配置は2つの因子を同時に調べられて効率的
- 二元配置なら、因子の「組み合わせ」による特別な効果(交互作用)も分かる
二元配置実験とは?定義と構造
📚 二元配置実験の定義
二元配置実験とは
2つの因子(例えば肉の種類とスパイス量)を同時に変えたとき、結果にどう影響するかを調べる実験。
二元配置実験では、以下の3つの効果を評価できます:
🍛 実験例:カレーの味評価
今回は、カレーの美味しさを例に考えてみましょう。
調べたい因子は以下の2つです:
- 因子A:肉の種類(水準1:豚肉、水準2:牛肉)
- 因子B:スパイス量(水準1:少、水準2:多)
この2つの因子を組み合わせると、2×2=4通りの条件ができます。
各条件で2回ずつ測定(繰り返し)するので、合計8個のデータを取得します。
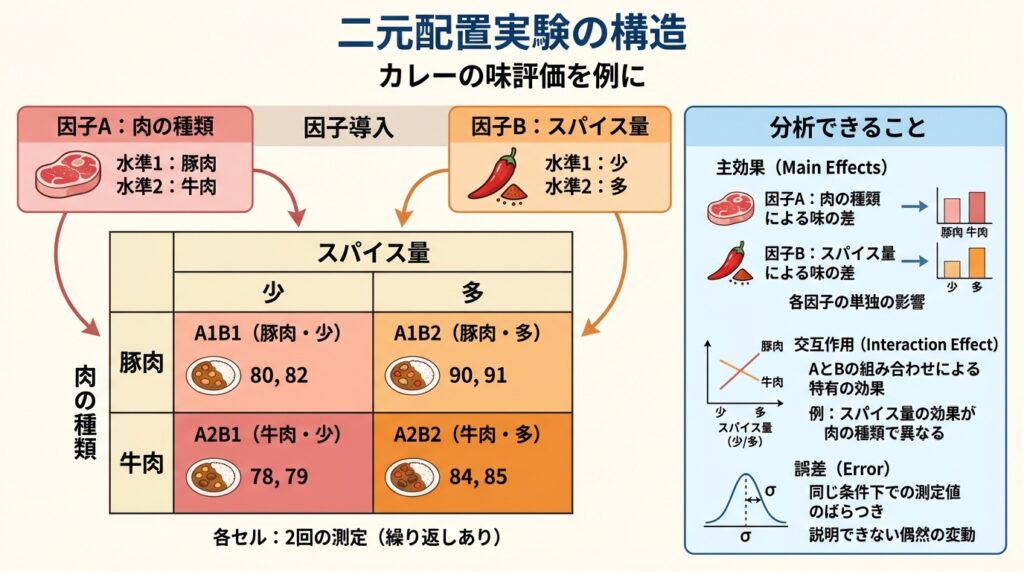
🔍 データの読み方
- 豚肉×スパイス少:80点と82点(平均81.0)
- 豚肉×スパイス多:90点と91点(平均90.5)
- 牛肉×スパイス少:78点と79点(平均78.5)
- 牛肉×スパイス多:84点と85点(平均84.5)
→ 豚肉×スパイス多の組み合わせが、平均90.5点で最も高評価ですね!
主効果と交互作用の違い
二元配置実験で最も重要なのが、「主効果」と「交互作用」の理解です。
これが分かれば、実験結果を正しく解釈できます!
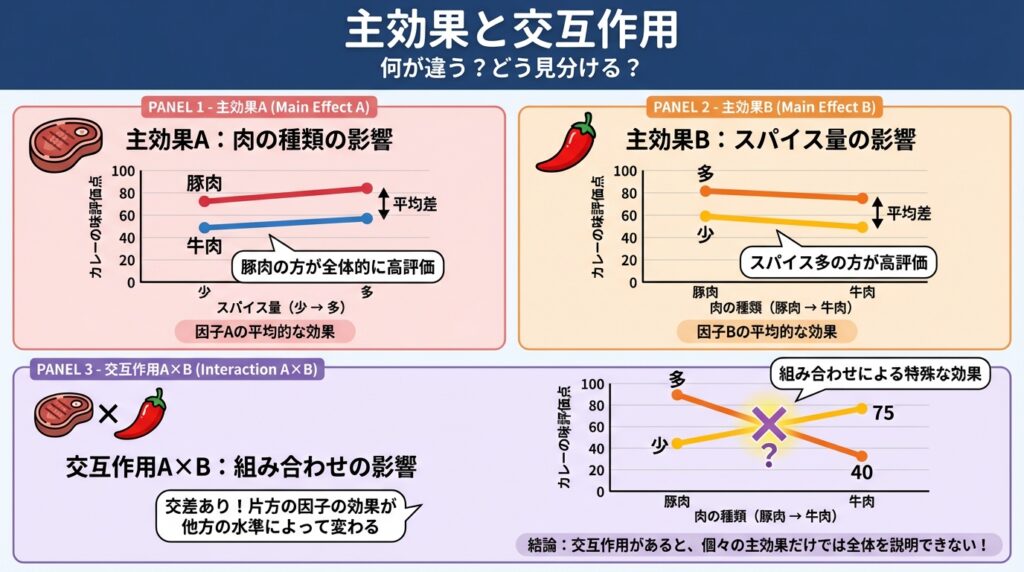
📊 主効果とは?
主効果とは、各因子が単独で与える影響のことです。
主効果A(肉の種類)
スパイス量に関わらず、豚肉と牛肉で平均的にどれだけ差があるか
主効果B(スパイス量)
肉の種類に関わらず、スパイス少と多で平均的にどれだけ差があるか
✕ 交互作用とは?
交互作用とは、因子の組み合わせによって生まれる特別な効果のことです。
交互作用A×B
「豚肉×スパイス多」という特定の組み合わせが特別に美味しい!
→ これは主効果だけでは説明できない相乗効果です
☕ コーヒーブレイク
交互作用の見分け方は簡単!
グラフで2本の線が平行なら交互作用なし、交差したり大きく離れたら交互作用ありです。
図3を見ると、豚肉の線の傾きが牛肉より急なので、交互作用があると分かりますね!
二元配置分散分析の計算手順(8ステップ)
それでは、実際に分散分析(ANOVA)を行って、主効果と交互作用が統計的に有意かどうかを検定しましょう!
計算は8つのステップに分けて進めます。
一つひとつ丁寧に見ていきましょう!
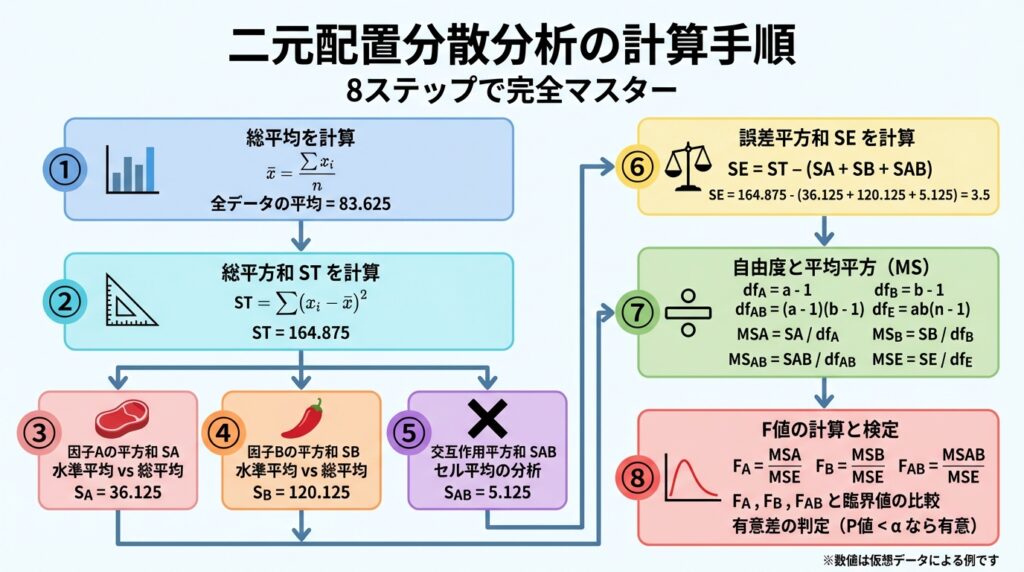
① 総平均を計算
まず、全データの平均を求めます。
総平均 = (80 + 82 + 90 + 91 + 78 + 79 + 84 + 85) ÷ 8 = 83.625
② 総平方和 ST を計算
総平方和は、各データと総平均との差を2乗して合計します。
ST = Σ(xi - x̄)²
各データごとに計算すると:
- (80 - 83.625)² = 13.14
- (82 - 83.625)² = 2.64
- (90 - 83.625)² = 40.14
- (91 - 83.625)² = 54.14
- (78 - 83.625)² = 31.64
- (79 - 83.625)² = 21.14
- (84 - 83.625)² = 0.14
- (85 - 83.625)² = 1.89
ST = 164.875
③ 因子A(肉の種類)の平方和 SA
まず、各水準の平均を求めます:
- 豚肉の平均:(80 + 82 + 90 + 91) ÷ 4 = 85.75
- 牛肉の平均:(78 + 79 + 84 + 85) ÷ 4 = 81.5
因子Aの平方和は、各水準の平均と総平均との差から計算します:
SA = 4 × [(85.75 - 83.625)² + (81.5 - 83.625)²]
SA = 4 × (4.516 + 4.516) = 36.125
④ 因子B(スパイス量)の平方和 SB
同様に、スパイス量の各水準の平均を求めます:
- スパイス少の平均:(80 + 82 + 78 + 79) ÷ 4 = 79.75
- スパイス多の平均:(90 + 91 + 84 + 85) ÷ 4 = 87.5
SB = 4 × [(79.75 - 83.625)² + (87.5 - 83.625)²]
SB = 4 × (15.016 + 15.016) = 120.125
⑤ 誤差平方和 SE を計算
誤差平方和は、各データとそのセル平均との差から計算します。
例えば、豚肉×スパイス少のセル平均は81.0なので:
- (80 - 81.0)² = 1.0
- (82 - 81.0)² = 1.0
全てのセルで同様に計算して合計すると:
SE = 1.0 + 1.0 + 0.25 + 0.25 + 0.25 + 0.25 + 0.25 + 0.25 = 3.5
⑥ 交互作用平方和 SAB を計算
交互作用の平方和は、残り成分として計算します:
SAB = ST - SA - SB - SE
SAB = 164.875 - 36.125 - 120.125 - 3.5 = 5.125
💡 平方和の分解
ST = SA + SB + SAB + SE
164.875 = 36.125 + 120.125 + 5.125 + 3.5 ✓
⑦ 各分散(平均平方)を計算
- 因子Aの自由度:2 - 1 = 1
- 因子Bの自由度:2 - 1 = 1
- 交互作用の自由度:(2-1) × (2-1) = 1
- 誤差の自由度:8 - 4 = 4
VA = 36.125 ÷ 1 = 36.125
VB = 120.125 ÷ 1 = 120.125
VAB = 5.125 ÷ 1 = 5.125
VE = 3.5 ÷ 4 = 0.875
⑧ F値を計算して検定
最後に、F値を計算して、各効果が統計的に有意かどうかを判定します:
F = 各因子の分散 ÷ 誤差分散
FA = 36.125 ÷ 0.875 = 41.3 ✅ 有意!
FB = 120.125 ÷ 0.875 = 137.3 ✅ 有意!
FAB = 5.125 ÷ 0.875 = 5.857 ✅ 有意!
🎉 結果の解釈
すべてのF値が大きいので、以下が統計的に有意です:
✅ 肉の種類は味に影響する
✅ スパイス量は味に影響する(効果が最大!)
✅ 肉とスパイスの組み合わせにも特別な効果がある
分散分析表の見方と結果の解釈
計算結果を分散分析表にまとめると、一目で結果が分かります!
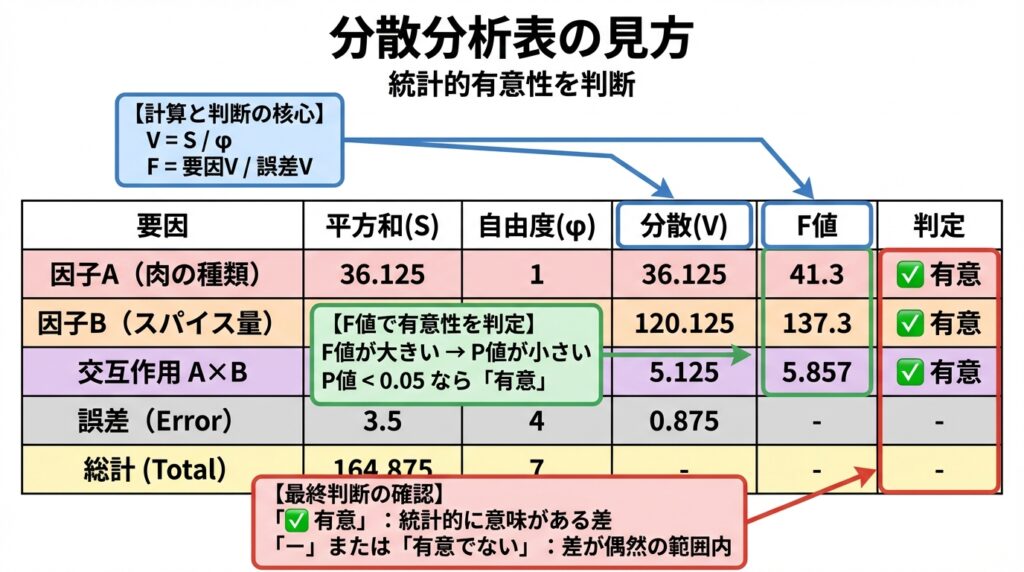
📊 この結果から分かること
- スパイス量の効果が最大(F=137.3)
→ スパイスを増やすと味が大きく向上! - 肉の種類も重要(F=41.3)
→ 豚肉の方が牛肉より高評価 - 交互作用あり(F=5.857)
→ 「豚肉×スパイス多」の組み合わせが特別に美味しい!
まとめ:二元配置実験の強み
📝 この記事のまとめ
- 二元配置実験は2つの因子を同時に調べられる効率的な手法
- 主効果は各因子の単独の影響、交互作用は組み合わせの特別な効果
- 計算は8ステップ:平方和の分解 → 分散の計算 → F検定
- 分散分析表を見れば、どの効果が統計的に有意かすぐに分かる
- 一元配置より情報量が多く、実践的!
二元配置実験をマスターすれば、実験計画法の世界がぐっと広がります!
次のステップでは、さらに多くの因子を効率的に調べられる「直交配列表」について学びましょう!
🔗 あわせて読みたい関連記事
📊 一元配置実験の基礎
まずはシンプルな一元配置から学ぶ
記事を読む →
✕ 交互作用とは?
組み合わせの特別な効果を深掘り
記事を読む →
📐 平方和の基礎
分散分析の計算の土台を理解
記事を読む →
📚 実験計画法をもっと学びたいあなたへ
当サイトでは、実験計画法(DOE)の基礎から実践まで、初心者でも分かりやすく解説しています。
品質管理や統計的品質管理に興味がある方は、ぜひ他の記事もチェックしてみてください!