こんにちは、シラスです。
前回、回帰分析とは「未来を予測するために、データの中に一本の直線を引くことだ」とお話ししました。
しかし、ここで一つ疑問が湧きます。
適当に定規で引いてるわけじゃないよね?」
もちろん、適当ではありません。
統計学では、ある数学的なルールに従って、世界でたった一本の「最もふさわしい線」を計算で導き出しています。
そのルールの名前が、「最小二乗法(さいしょうにじょうほう)」です。
今日は、この少し難しそうな名前の手法について、数式をほとんど使わず、「バネの力」に例えて直感的に解説します。
目次
1. 「良い線」とは何か?
バラバラに散らばった点(データ)の中に直線を引くとき、どんな線が「良い線」だと思いますか?
おそらく、多くの人がこう答えるでしょう。
正解です。
つまり、「点と線のズレ(距離)」ができるだけ小さい線が、理想的な回帰直線です。
2. ズレをどう計算する?(残差の話)
この「点と線のズレ」のことを、専門用語で「残差(ざんさ)」と呼びます。
「じゃあ、すべての点の残差を足し算して、それが最小になる線を探せばいいじゃん!」
そう思うかもしれませんが、これには大きな落とし穴があります。
⚠️ 単純に足し算してはいけない理由
線の「上にある点」はプラス(+3cm)、線の「下にある点」はマイナス(-3cm)になります。
これらを単純に足すと、プラスとマイナスが打ち消し合って「合計ゼロ」になってしまうのです。
(めちゃくちゃズレているのに、計算上はズレていないことになってしまう!)
3. 解決策:二乗してプラスにする
マイナスを消すためにどうするか?
統計学者が選んだ方法は、「二乗する」ことでした。
- $(+3)^2 = 9$
- $(-3)^2 = 9$
これなら、上でも下でも「プラスの数字」として評価できます。
そして、全ての点の「残差の二乗」を合計し、それが最小(ミニマム)になるような線を引く。
これが「最小二乗法(Least Squares Method)」の名前の由来です。
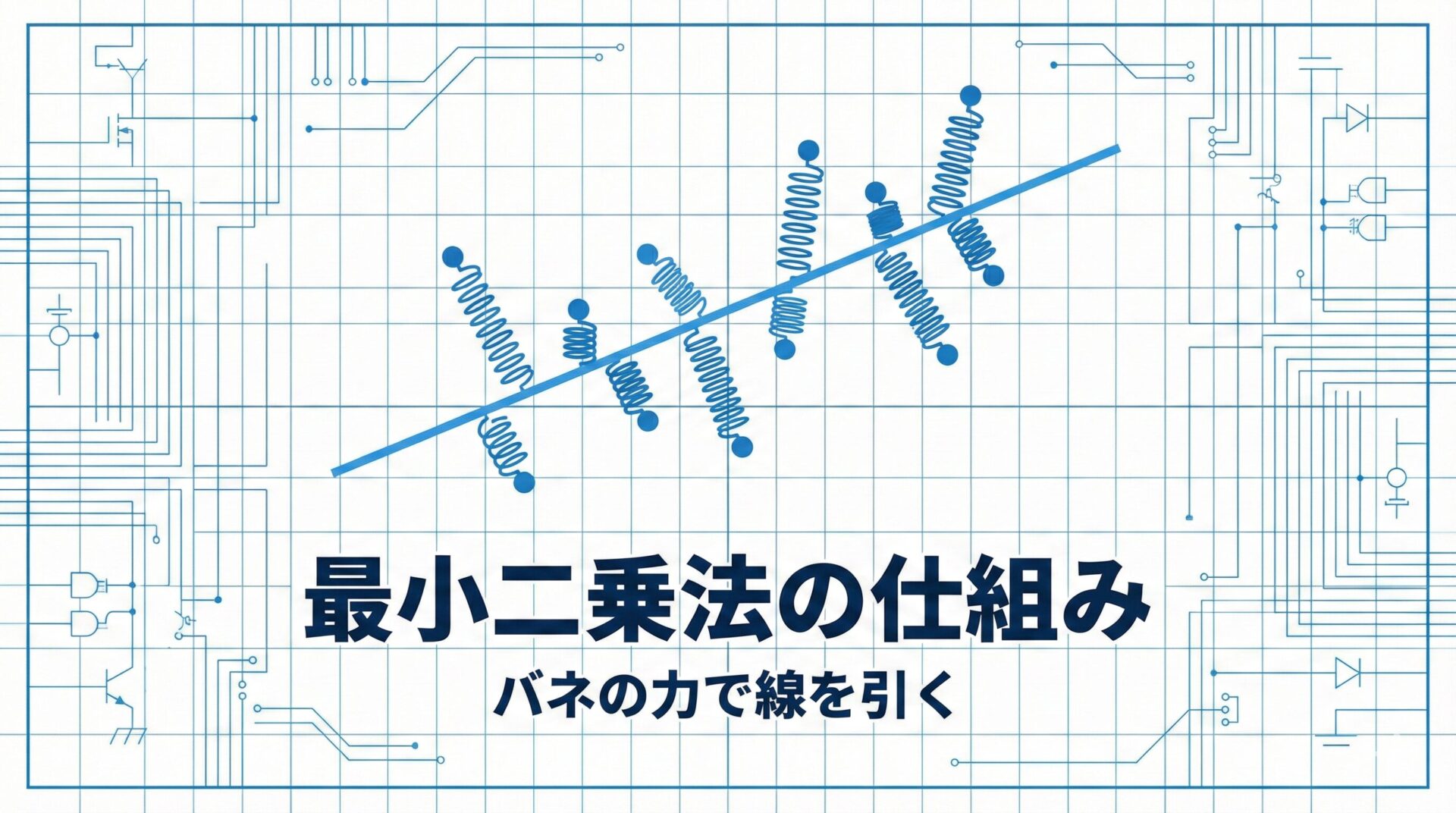
4. イメージ図解:バネの力で安定させる
数式の話ばかりだと疲れるので、物理的なイメージで捉えてみましょう。
回帰直線は、「バネで吊るされた棒」のようなものです。
🔩 物理的な安定点
① 散らばった点(データ)の一つ一つに「バネ」が付いていると想像してください。
② そのバネを、一本の「棒(直線)」に繋ぎます。
③ 手を離すと、棒はバネに引っ張られて動きますが、最終的に「力が釣り合う場所」でピタッと止まります。
二乗するということは、「遠くにある点ほど、強力なバネ(強い力)で棒を引っ張る」という意味になります。
だから、外れ値(極端に離れた点)があると、直線はそっちにグイッと引っ張られてしまうのです。
まとめ
この計算によって、誰がやっても世界でたった一本の「最適な予測線」が引けるようになります。
さて、線を引くことはできました。
しかし、その線が「どれくらい信用できるのか?」は別の話です。
「気温で売上を予測できる!」と言っても、その精度がボロボロだったら意味がありませんよね?
次回は、回帰分析の通知表とも言える指標、「決定係数($R^2$)」について解説します。
📚 回帰分析を「武器」にする3冊
数式アレルギーだった私でも読破できた、厳選の良書です。