📌 この記事の位置づけ
「実験計画法の基礎概念シリーズ」第11回。前回は「誤差」の正体を学びました。今回は混同しやすい「残差」と「誤差」の違いをスッキリ解説します。
「残差と誤差って、同じ意味じゃないの?」
「教科書で両方出てくるけど、使い分けがわからない…」
この2つ、似ているようで決定的に違います。
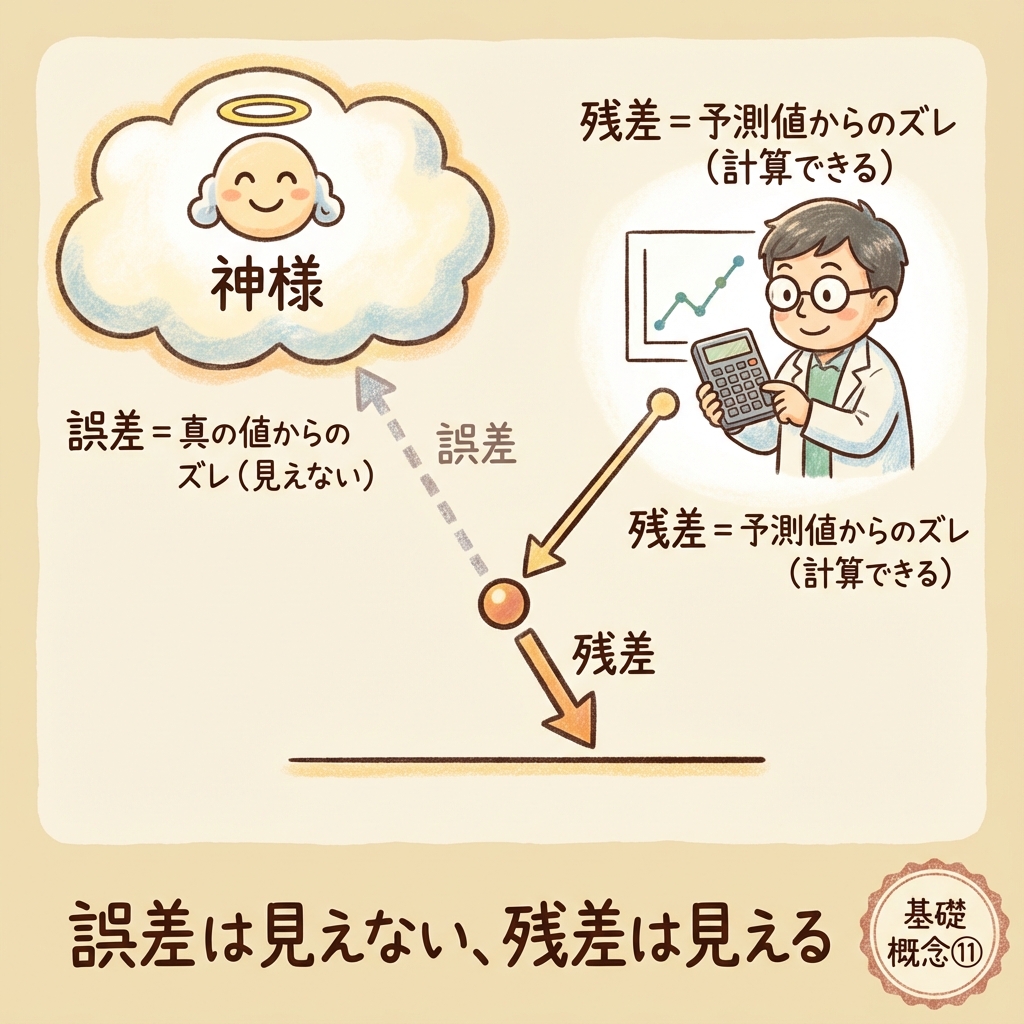
一言で言うと、誤差は「見えないズレ」、残差は「見えるズレ」です。
目次
結論:誤差は神様、残差は人間
まず結論をお伝えします。
誤差とは?【真の値からのズレ】
誤差とは、真の値(本当の値)と実測値の差です。
📖 誤差の定義
誤差 = 実測値 − 真の値
問題は、「真の値」は誰にもわからないこと。
だから誤差は計算できない。
🤔 なぜ真の値はわからないのか?
たとえば、ある部品の「本当の長さ」を測りたいとします。
10回測定しました。
📏 10回の測定結果(mm)
10.02, 9.98, 10.01, 9.99, 10.03, 10.00, 9.97, 10.02, 10.01, 9.99
平均は10.002mm。でも「本当の長さ」は10.002mmなの?
平均値は10.002mmですが、これが「真の値」かどうかはわかりません。
もし100回測ったら、平均は10.001mmになるかもしれない。1000回なら10.0005mmかもしれない。
無限回測定しないと「真の値」には辿り着けないのです。だから誤差は「神様だけが知る値」なのです。
残差とは?【予測値からのズレ】
残差とは、予測値(モデルから計算した値)と実測値の差です。
📖 残差の定義
残差 = 実測値 − 予測値
予測値は計算で求められる。
だから残差は計算できる。
📊 具体例:カレーの実験で考える
カレーの実験で、「牛肉×スパイス多め」の条件を3回繰り返したとします。
| 回 | 実測値 | 予測値(平均) | 残差 |
|---|---|---|---|
| 1回目 | 88点 | 90点 | −2 |
| 2回目 | 92点 | 90点 | +2 |
| 3回目 | 90点 | 90点 | 0 |
予測値(この場合は平均値90点)からのズレが残差です。
残差は実際のデータから計算できるので、分析に使えるのです。
誤差と残差の関係
誤差は計算できないので、私たちは残差を使って誤差を「推定」します。
誤差と残差の関係
分散分析では、残差の平方和を使って「誤差分散」を推定します。
残差は誤差の「代理」として働いてくれるのです。
比較表で整理
| 項目 | 誤差(Error) | 残差(Residual) |
|---|---|---|
| 定義 | 実測値 − 真の値 | 実測値 − 予測値 |
| 基準となる値 | 真の値(わからない) | 予測値(計算できる) |
| 計算可能? | ❌ できない | ⭕ できる |
| イメージ | 神様だけが知る値 | 人間が計算できる値 |
| 用途 | 理論上の概念 | 誤差の推定・モデル診断 |
なぜ残差を分析するのか?
残差を分析することで、以下のことがわかります。
✅ 残差分析でわかること
- モデルが適切か?:残差に偏りがあればモデルに問題あり
- 外れ値はないか?:極端に大きい残差は外れ値の可能性
- 誤差の大きさは?:残差から誤差分散を推定できる
分散分析表の「誤差」の行に出てくる値は、実は残差から計算した推定値なのです。
まとめ
📌 この記事のポイント
- 誤差=真の値からのズレ(神様だけが知る、計算できない)
- 残差=予測値からのズレ(人間が計算できる)
- 誤差は計算できないので、残差で誤差を推定する
- 分散分析の「誤差」は、実は残差から推定した値
次の記事では、「交絡」について解説します。因子が混ざり合って「真犯人」がわからなくなる危険な現象です。
📚 次に読む記事
「アイスが売れると水難事故が増える」——でもアイスが事故の原因じゃないですよね?複数の因子が混ざり合って「真犯人」がわからなくなる現象、それが「交絡」です。
交絡とは?|基礎概念⑫ →関連記事【あなたの悩みを解決】
🤔「誤差の基本を復習したい」
→ 誤差とは?実験で避けられないバラつきの正体|基礎概念⑩🤔「残差の検討(残差分析)のやり方を知りたい」
→ 残差の検討(残差分析)|実験の「健康診断」を行う🤔「回帰分析での残差について詳しく知りたい」
→ 【完全図解】残差と誤差の違い|見えるズレと見えないズレを徹底解説🤔「分散分析表の作り方を知りたい」
→ 一元配置実験の計算方法を完全図解|分散分析表を1から作る全手順🤔「群間平方和と群内平方和の分解を知りたい」
→ 群間平方和と群内平方和の分解|データを「効果」と「誤差」に切り分ける🤔「実験計画法の全体像を把握したい」
→ 【完全版】実験計画法の学習マップ|基礎から応用まで体系的に学ぶ🤔「QC検定対策として学びたい」
→ 【合格体験記】知識ゼロから半年でQC検定2級に合格した勉強法🤔「不偏分散について詳しく知りたい」
→ 不偏分散はなぜn-1で割る?バラつき過小評価の正体