こんにちは、シラスです。
SNSを見ていると、こんな投稿が流れてくることがあります。
「えっ、待って。無料10連でSSR3枚抜きしたんだけど!?今年の運使い果たしたかも😭✨」
#神引き #ガチャ
これを見て、「うわぁ、すごい確率!選ばれた人間だ!」と羨ましくなるかもしれません。
一方で、自分のガチャ結果を見て「なんで自分だけ爆死するんだ…」と落ち込むこともあるでしょう。
しかし、統計学的に見れば、この神引きは「奇跡」でも何でもありません。
何万人ものプレイヤーがいれば、誰かには「必ず(必然的に)」起こる現象なのです。
今日は、ガチャという身近な運試しを題材に、確率のカラクリと人間の心理バイアスについて解説します。
1. 「1%」の本当の意味
まず、ガチャの確率計算をしてみましょう。
例えば、SSR(最高レア)の排出率が「1%」だとします。
「100回引けば1回は当たるだろう」
多くの人は直感的にそう考えますが、現実はもっとシビアです。
100連で1枚も当たらない確率
$(0.99)^{100} \approx 0.366$
つまり、約37%(3人に1人)は爆死します。
逆に言えば、63%の人は当たります。
しかし、「3人に1人は1万円使っても何も得られない」というのは、確率的にはごくありふれた日常なのです。
2. 「10連で3枚抜き」の確率は?
では、冒頭の「10連で1%のSSRが3枚出る」確率はどれくらいでしょうか?
これは「二項分布」を使って計算できます。
- 計算式: $_{10}C_3 \times (0.01)^3 \times (0.99)^7$
- 答え: 約 0.00011
- パーセント: 約 0.01%(1万人に1人)
「0.01%!やっぱり奇跡じゃないか!」
そう思いますよね。
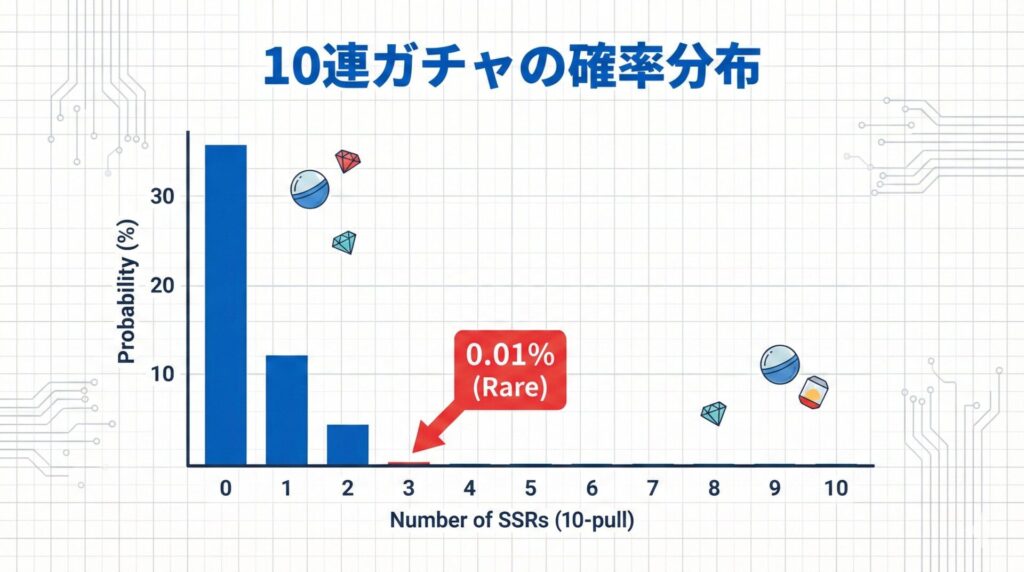
しかし、ここで視点を「個人」から「全体」に変えてみましょう。
プレイヤー数という分母
人気ゲームのアクティブユーザー数が100万人だと仮定します。
全員が10連ガチャを一回引いたとしたら、どうなるでしょうか?
なんと、100人ものプレイヤーが「10連3枚抜き」を達成することになります。

その100人のうち、何人かが嬉しくてSNSにスクショを投稿します。
あなたのタイムラインに「神引き報告」が流れてくるのは、奇跡でも何でもなく、「大数の法則(試行回数の暴力)」による必然なのです。
3. なぜ「自分だけ運が悪い」と感じるのか?
SNSでは神引きばかりが目立ちますが、その裏には「何も当たらなかった99.99%の沈黙」があります。
- 当たった人は、嬉しくて投稿する(生存者バイアス)。
- 外れた人は、何も投稿しない(死人に口なし)。
このフィルターを通した情報だけを見ていると、脳が錯覚を起こします。
「みんな当たってるのに、なんで俺だけ…」
いいえ、安心してください。
あなたと同じように外れた何十万人もの同志たちが、画面の向こうで静かにスマホを閉じているのです。
まとめ
確率の仕組みを知っていれば、他人の神引きを見ても「ああ、今日は君の番だったんだね」と冷静でいられます。
そして、自分が爆死しても「まあ、37%の確率で起きる普通の現象だしな」とダメージを減らせます。
統計学は、感情が揺さぶられがちな現代社会において、心を平穏に保つための「精神安定剤」にもなるのです。
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


