こんにちは、シラスです。
統計データを見るときに出てくる「決定係数($R^2$)」。
教科書には「回帰変動を全変動で割ったもの」と難しく書かれていますが、もっと直感的なイメージで捉えてみましょう。
今回は数式を一切使わず、「メーター」と「面積」でその正体を視覚化します。
1. 視覚で見る「0〜1」の評価基準
決定係数は、あなたの作った予測モデルの「的中精度メーター」だと思ってください。
予測線の上に全てのデータが乗っている状態。現実にはほぼあり得ない「神の予言」。
実務レベルで「使える」ライン。傾向がはっきりと読み取れる。
予測式が全く役に立っていない。サイコロを振っているのと同じ。
2. 正体は「解明できた謎の割合」
なぜ「寄与率」とも呼ばれるのか?
それは、$R^2$ が「データのバラつき(謎)」のうち、どれだけ原因を特定できたかを表しているからです。
例えば、「ラーメン屋の売上のバラつき」を分析するとします。
📊 売上の変動(全データのバラつき)
■ 青い部分: あなたの計算式で説明がついた部分(気温が暑いから売れた、寒いから売れた)。
■ 灰色の部分: 計算式では説明できない誤差(たまたま団体客が来た、店長の機嫌など)。
つまり、青い部分(説明できた部分)が多ければ多いほど、決定係数は1に近づきます。
逆に、灰色の部分(謎の誤差)ばかりだと、決定係数は0に近づきます。
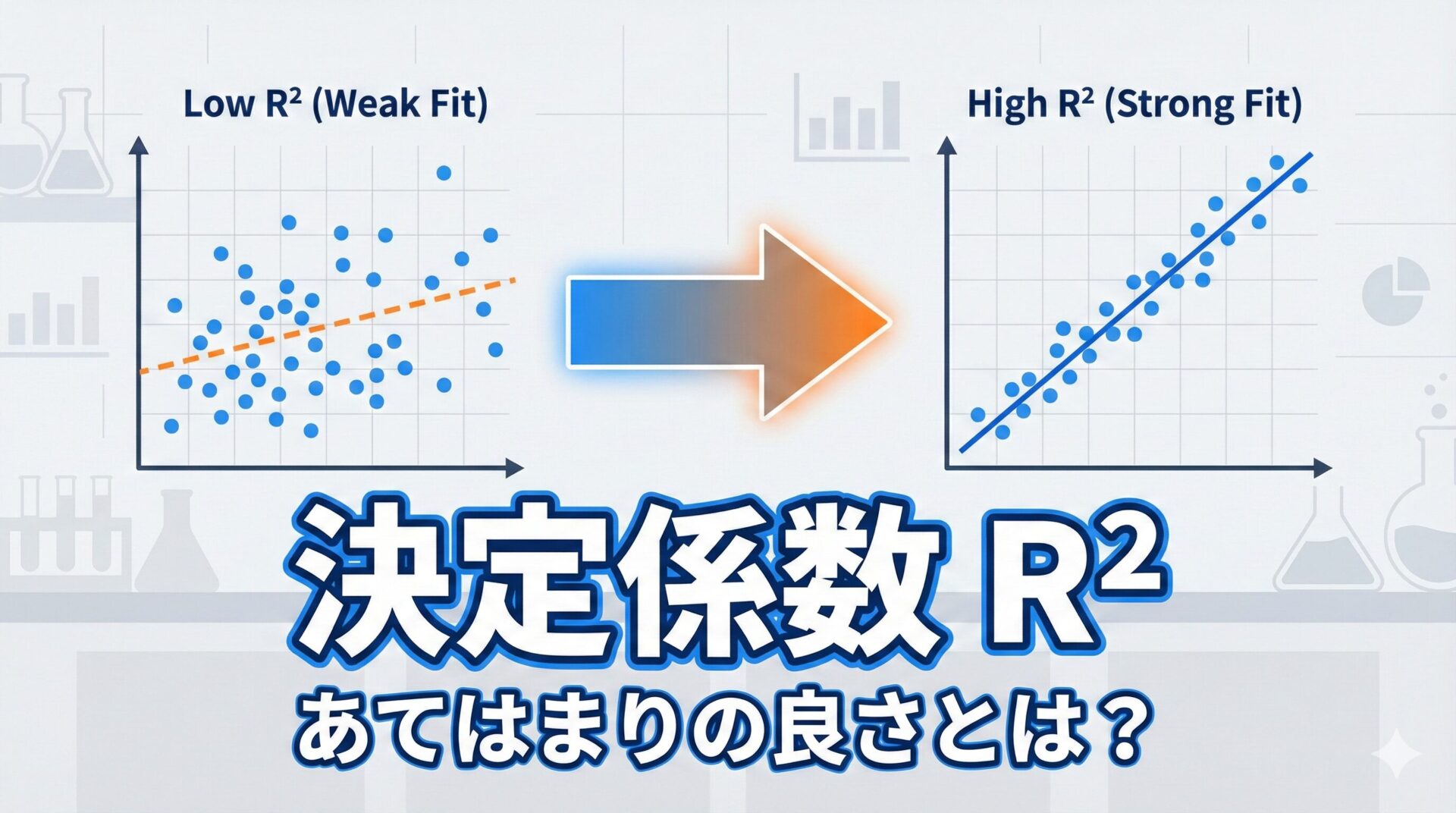
3. グラフでの見た目比較
実際にグラフにしたとき、決定係数の違いは「点の散らばり具合」として現れます。
$R^2$ が高い (0.9)
点が予測線(直定規)の周りに
「ビシッ!」と集まっている。
予測線を使えば、未来を高精度で当てられる。
$R^2$ が低い (0.2)
点が予測線の周りに
「バラバラ」に散らばっている。
この線を信じて予測すると大怪我をする。
まとめ
- $R^2$ は「的中精度メーター」: 1に近いほど優秀。
- 正体は「面積の割合」: データのバラつきのうち、「理由がわかった部分」の割合。
- 目安: 0.8以上ならかなり信頼できる。0.2以下なら作り直し。
難しい数式を覚える必要はありません。
Excelで $R^2$ を見たら、この「青とグレーのバー」を頭に思い浮かべて、「どれくらい謎が解明できたかな?」と考えてみてください。