✅ こんな悩みを抱えていませんか?
- 「∮H・dlって何を積分してるの?」
- 「アンペールの法則の物理的意味がわからない…」
- 「ソレノイドの磁界計算が苦手…」
電験三種の「理論」科目で頻出するアンペールの周回積分の法則。特にソレノイドの磁界計算は、毎年のように出題される超重要テーマです。
でも安心してください。この記事では、∮H・dl = NI の物理的意味から、無限長ソレノイド・環状ソレノイドの磁界計算まで、まるで目の前で見ているような図解で完全解説します。
💡 この記事で完全マスターできること
- アンペールの周回積分の法則の物理的意味
- 無限長ソレノイドの磁界 H = nI の導出
- 環状ソレノイドの磁界 H = NI/(2πr) の計算
- 試験で狙われる実践計算問題の解法
それでは、磁界の「渦」を一周なぞる「見えない積分」を、一緒に可視化していきましょう!
目次
📐 アンペールの周回積分の法則とは?
📖 法則の数式表現
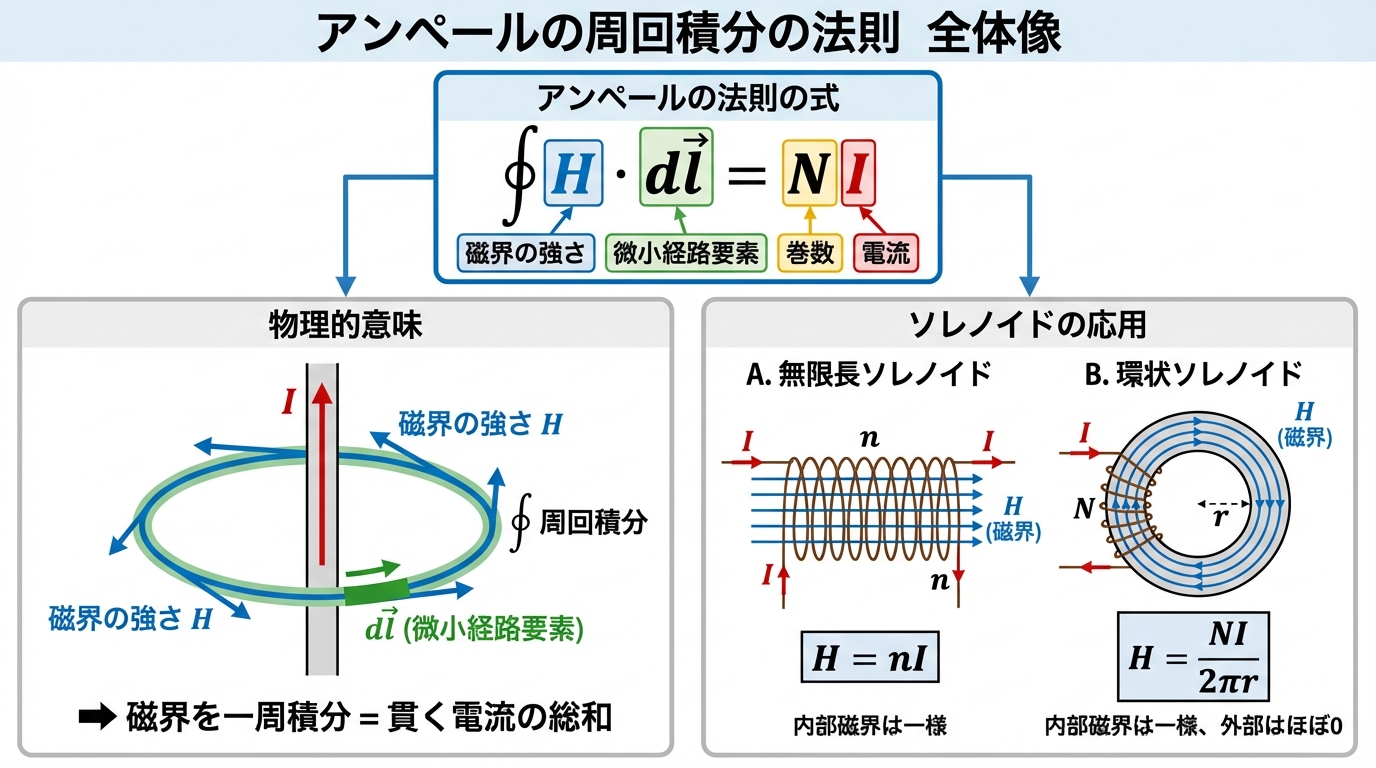
⚡ アンペールの周回積分の法則
∮H・dl = NI
(磁界Hを閉曲線に沿って一周積分 = 閉曲線を貫く電流の総和)
この式の各記号の意味を確認しましょう。
| 記号 | 意味 | 単位 |
|---|---|---|
| ∮ | 閉曲線に沿った周回積分 | — |
| H | 磁界の強さ(ベクトル) | A/m |
| dl | 経路の微小線素(ベクトル) | m |
| N | 閉曲線を貫く導体の数(巻数) | 回 |
| I | 1本あたりの電流 | A |
🔍 物理的意味を理解する
アンペールの法則の物理的意味を、左辺と右辺に分けて見ていきましょう。
⚡ 左辺 ∮H・dl の意味
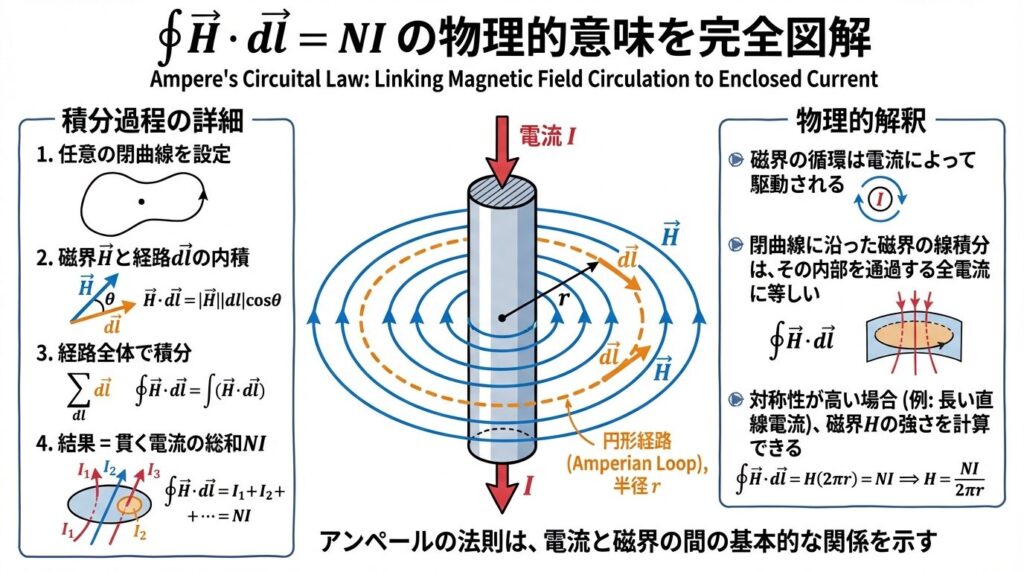
- 任意の閉曲線を設定する(どんな形でもOK)
- 閉曲線に沿って磁界Hを一周なぞる(周回積分)
- H・dlは内積(Hの接線成分×dlの長さ)
- これを一周分足し合わせる = 磁界の「渦」の強さ
⚡ 右辺 NI の意味
- 閉曲線を貫く電流の総和
- N本の導体がそれぞれI [A]流れている → 合計NI [A]
- 閉曲線の外側の電流は関係ない!
- 電流の向きが逆なら符号が逆(相殺される)
💡 イメージで覚えよう
アンペールの法則 = 渦巻きの強さ測定器
磁界の「渦」を閉曲線で一周ぐるっとなぞると、その強さは渦の中心を貫く電流の量で決まる!というルールです。
⚙️ アンペールの法則の使い方
アンペールの法則を使って磁界Hを求める一般的な手順は以下の通りです。
⚡ 磁界計算の3ステップ
- Step1: 周回経路を設定 → Hが一定で、経路に平行or垂直になる経路を選ぶ
- Step2: 左辺を計算 → ∮H・dlを経路に沿って計算(平行部分だけ寄与)
- Step3: 等式を解く → ∮H・dl = NI からHを求める
それでは、この手順を無限長ソレノイドに適用してみましょう!
🔋 無限長ソレノイドの磁界 H = nI
📖 無限長ソレノイドとは?
無限長ソレノイドとは、非常に長い円筒状のコイルのこと。長さが直径に比べて十分長い場合、内部の磁界は一様(どこでも同じ)になります。
⚡ 無限長ソレノイドの特徴
- 内部磁界: 一様(軸方向に平行)
- 外部磁界: ほぼゼロ(漏れ磁束なし)
- 磁界の強さ: 巻数密度nと電流Iのみで決まる
- 長さに依存しない!
🔬 H = nI の導出
アンペールの法則を使って、無限長ソレノイドの内部磁界Hを導出します。
⚡ 無限長ソレノイドの磁界導出
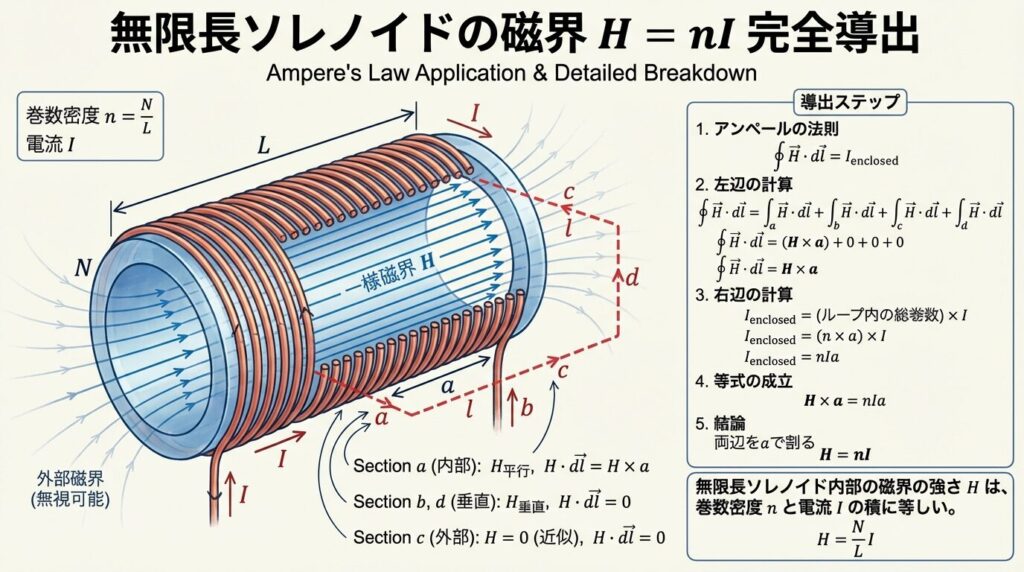
- Step1: 周回経路を設定
→ ソレノイド内部に長さaの辺を持つ長方形ループを設定
→ 辺a(内部・軸方向)、辺b・d(垂直)、辺c(外部) - Step2: 左辺 ∮H・dl を計算
→ 辺a: Hは平行で一定 → H・dl = H×a
→ 辺b・d: Hは垂直 → H・dl = 0
→ 辺c: 外部でH≈0 → 0
→ 合計: ∮H・dl = H×a - Step3: 右辺 NI を計算
→ 長さaの区間にn×a回のコイルが貫く
→ 各コイルにI [A]流れている
→ 合計: NI = (n×a)×I - Step4: 等式を解く
→ H×a = (n×a)×I
→ aで割ると → H = nI [A/m]
💡 H = nI の重要ポイント
- n = N/L: 巻数密度(1mあたりの巻数) [回/m]
- I: コイルに流れる電流 [A]
- ソレノイドの長さLは関係ない!(nに含まれる)
- 内部磁界は一様(どこでも同じ値)
✏️ 練習問題①(無限長ソレノイド)
📖 例題
長さ0.5 mの無限長ソレノイドに、500回のコイルが巻かれている。このコイルに2 Aの電流を流したとき、内部の磁界の強さHを求めよ。
✅ 解答と解説
【解答】
Step1: 巻数密度nを計算
n = N/L = 500 / 0.5 = 1000 回/m
Step2: H = nI に代入
H = 1000 × 2 = 2000 A/m
答え: H = 2000 A/m
🍩 環状ソレノイドの磁界 H = NI/(2πr)
📖 環状ソレノイドとは?
環状ソレノイド(トロイダルコイル)とは、ドーナツ型のコイルのこと。磁界がトーラス内部に完全に閉じ込められるため、外部への漏れ磁束がありません。
⚡ 環状ソレノイドの特徴
- 磁界はトーラス内部に集中(外部磁界ゼロ)
- 磁界は円周方向(トーラスの中心軸周りに周回)
- 半径rが小さいほど磁界が強い
- 変圧器やインダクタに応用
🔬 H = NI/(2πr) の導出
アンペールの法則を使って、環状ソレノイドの内部磁界Hを導出します。
⚡ 環状ソレノイドの磁界導出
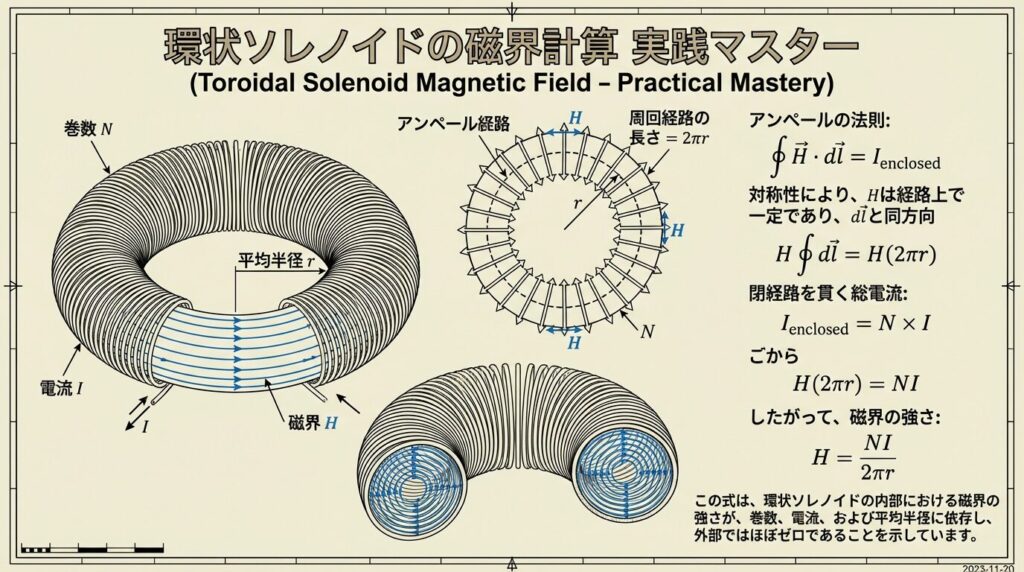
- Step1: 周回経路を設定
→ トーラスの中心軸から半径rの位置に円形ループを設定
→ 周回経路の長さ = 2πr - Step2: 左辺 ∮H・dl を計算
→ Hは経路に平行で一定
→ ∮H・dl = H × 2πr - Step3: 右辺 NI を計算
→ 円形ループをN回のコイルが全て貫く
→ 各コイルにI [A]流れている
→ 合計: NI - Step4: 等式を解く
→ H × 2πr = NI
→ H = NI/(2πr) [A/m]
💡 H = NI/(2πr) の重要ポイント
- N: 総巻数 [回]
- I: コイルに流れる電流 [A]
- r: トーラスの平均半径(中心軸からコイル中心まで) [m]
- rが小さいほどHは大きい(反比例)
✏️ 練習問題②(環状ソレノイド)
📖 例題
平均半径0.1 mの環状ソレノイドに、1000回のコイルが巻かれている。このコイルに2 Aの電流を流したとき、内部の磁界の強さHを求めよ。
✅ 解答と解説
【解答】
Step1: 公式に代入
H = NI/(2πr)
H = (1000 × 2) / (2π × 0.1)
H = 2000 / (2 × 3.14 × 0.1)
H = 2000 / 0.628
H ≈ 3183 A/m
答え: H ≈ 3183 A/m
📊 無限長vs環状の比較
| 項目 | 無限長ソレノイド | 環状ソレノイド |
|---|---|---|
| 形状 | 直線状(円筒) | ドーナツ状(トーラス) |
| 磁界の公式 | H = nI | H = NI/(2πr) |
| 使用するパラメータ | 巻数密度n [回/m] | 総巻数N [回]、半径r [m] |
| 内部磁界 | 一様(軸方向) | 円周方向(rで変化) |
| 外部磁界 | ほぼゼロ | 完全にゼロ |
| 応用例 | 電磁石、リニアモータ | 変圧器、インダクタ |
📚 まとめ|アンペールの法則を完全攻略
✅ この記事で覚えるべき3つのポイント
- アンペールの周回積分の法則: ∮H・dl = NI(磁界の渦 = 貫く電流)
- 無限長ソレノイド: H = nI(n = N/L、内部磁界一様)
- 環状ソレノイド: H = NI/(2πr)(rで逆比例)
⚡ 試験で狙われる5つのポイント
- ∮H・dl = NIの物理的意味(閉曲線内の電流のみカウント)
- H = nIの導出過程(長方形ループを使う)
- 巻数密度n = N/Lの計算
- H = NI/(2πr)の導出過程(円形ループを使う)
- 無限長vs環状の違い(公式の使い分け)
アンペールの周回積分の法則は、磁界の「渦」を一周なぞるという直感的なイメージが重要です。周回経路の設定さえマスターすれば、ソレノイドの磁界計算は簡単に解けます!
この記事が、あなたの電験三種合格への一歩になれば嬉しいです。アンペールの法則を完全攻略して、理論科目を得点源にしましょう! ⚡✨