💡 こんな悩み、抱えていませんか?
- 「v = Vmsinωtって何?暗号にしか見えない…」
- 「瞬時値って聞くけど、イメージが全然わかない」
- 「位相差と初期位相…違いが混乱する!」
- 「公式は覚えたけど、実際に何を表してるのか理解できてない」
こんにちは、シラスです。
電験三種の「理論」で最初にぶつかる壁が、この交流の式 v = Vmsinωtですよね。
結論から言うと、この式は「ブランコが揺れる様子」を数式で表しただけなんです。
難しそうに見えますが、実は中学生でも理解できる内容です。 この記事では、「観覧車」「マラソン」「信号機」といった身近な例えを使って、交流の本質を徹底的にイメージできるように解説します。
✅ この記事を読めば...
- 瞬時値が「ブランコの高さ」でイメージできる
- v = Vmsinωtが「観覧車の動き」で理解できる
- 初期位相が「マラソンのスタート位置」で納得できる
- 位相差が「信号機のズレ」で感覚的につかめる
それでは、一緒に交流の世界を冒険しましょう!
目次
⚡ 瞬時値(しゅんじち)とは?|「今この瞬間」の電圧
まず、交流を理解する上で最も大切な「瞬時値」から見ていきましょう。
📌 瞬時値の定義
ある特定の時刻 t における、電圧や電流の値のこと
記号: v (小文字) または i (小文字)
🪁 ブランコで理解する「瞬時値」
瞬時値を理解するには、公園のブランコを想像してください。
🌟 ブランコの例え
- ブランコは前後に揺れ続けます → これが交流の「振動」
- 最高点まで振れる高さ → これが「最大値 Vm」
- 今この瞬間、ブランコがどの高さにいるか → これが「瞬時値 v」
💡 つまり、時計の針が動くように、瞬時値も常に変化し続けているのです。
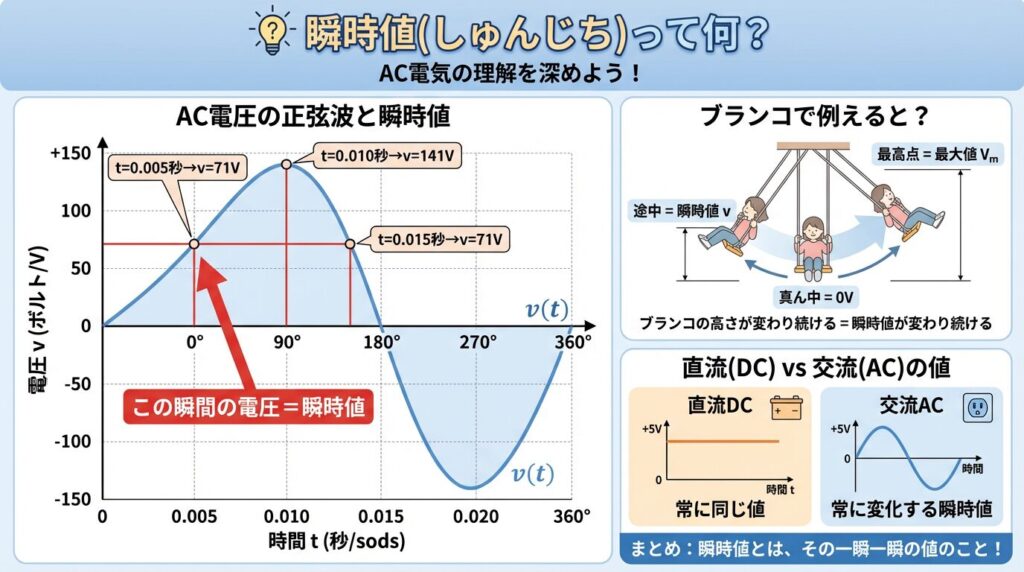
🔌 直流 vs 交流|何が違う?
ここで、直流と交流の決定的な違いを見てみましょう。
| 項目 | 直流 (DC) | 交流 (AC) |
|---|---|---|
| 電圧の変化 | 常に一定 (例: 100V) |
時々刻々と変化 (0V〜141V) |
| グラフの形 | 水平な直線 ━━━ | 波打つ曲線 ∿∿∿ |
| 瞬時値 | いつでも同じ値 | 時刻で変わる |
| 身近な例 | 乾電池 | 家のコンセント |
🔑 ここが重要!
直流は「止まっている看板」、交流は「回転している観覧車」です。
交流では「今どこにいるか?(瞬時値)」を常に意識する必要があるんですね。
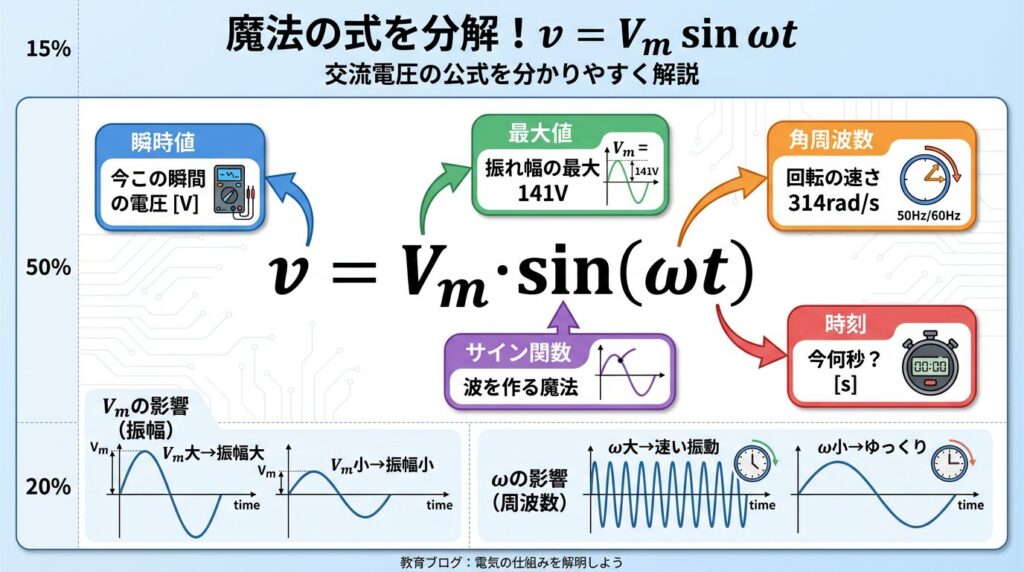
📐 魔法の式「v = Vmsinωt」を完全分解!
さあ、いよいよ交流の核心である瞬時値の式を分解していきましょう。
v = Vm sin ωt
この式1つで、交流の全ての動きがわかる!
🔍 式の各パーツを分解
📌 v (小文字) | 瞬時値
意味: 今この瞬間の電圧
例: 「t = 0.01秒のとき、v = 50V」のように、時刻によって変わる値
イメージ: ブランコが「今いる高さ」
📌 Vm (大文字+m) | 最大値
意味: 電圧が振れる最大の振り幅
例: 家庭用コンセント(AC100V)の場合、Vm ≈ 141V
イメージ: ブランコが一番高く振れたときの高さ
📌 sin (サイン) | 上下振動を作る魔法
意味: -1 〜 +1 の範囲で滑らかに振動する関数
役割: 直線的な「時間」を、波打つ「正弦波」に変換する
イメージ: 観覧車に乗って、高さが上下するような動き
📌 ω (オメガ) | 角周波数
意味: 1秒間に何ラジアン回転するか(振動の速さ)
公式: ω = 2πf (f は周波数 [Hz])
例: 日本の商用電源は f = 50Hz → ω = 314 rad/s
イメージ: 観覧車が回る速さ
📌 t (ティー) | 時刻
意味: 今何秒経過したか
単位: 秒 [s]
例: t = 0.01秒、t = 0.5秒 など
イメージ: ストップウォッチの針
🎯 式を日本語で読むと?
📣 「今この瞬間(t)の電圧(v)は、
最大値(Vm) × 角周波数(ω)と時刻(t)で決まる角度のサイン(sin)」
🧮 実際に計算してみよう!
📝 計算例題
家庭用コンセント(50Hz)の電圧を考えます。
最大値 Vm = 141V、角周波数 ω = 314 rad/s
問: t = 0.005秒 のとき、瞬時値 v はいくらか?
v = Vm sin ωt
v = 141 × sin(314 × 0.005)
v = 141 × sin(1.57)
v = 141 × 1.0 (※ sin(π/2) ≈ 1)
v ≈ 141V
✅ 答え: 約141V (ちょうど最大値!)
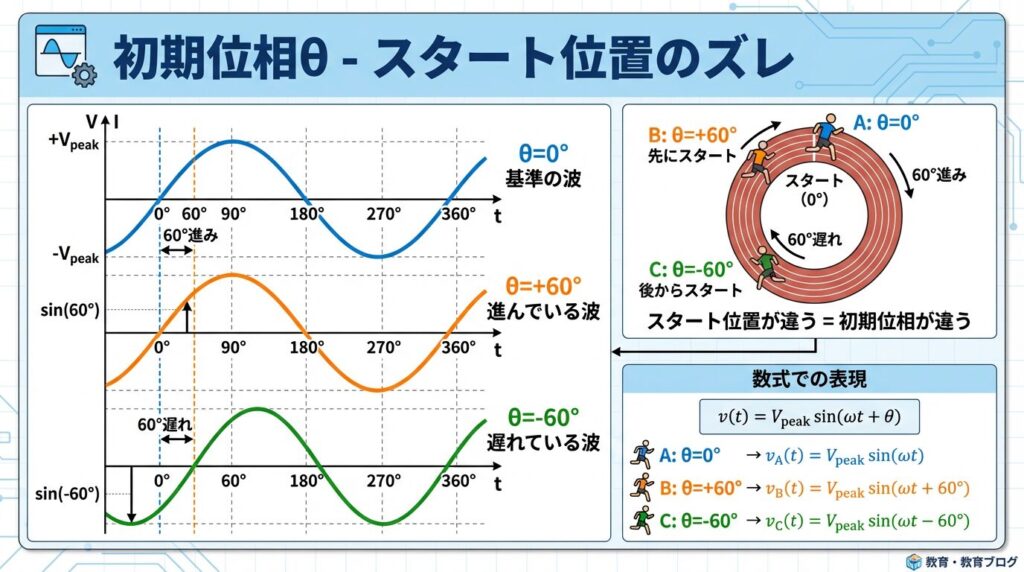
🔄 初期位相(θ)とは?| スタート位置のズレ
ここまでは v = Vmsinωt という基本形を見てきました。 しかし、実際の回路では「スタート位置がズレている」ケースがあります。
v = Vm sin (ωt + θ)
「+θ」が追加された!これが初期位相です
🏃 マラソンの例えで理解
🏁 3人のランナーがいます
- ランナーA (θ = 0°): スタートラインに立っている
- ランナーB (θ = +60°): スタートラインより60m先にいる(進んでいる)
- ランナーC (θ = -60°): スタートラインより60m手前にいる(遅れている)
💡 スタート位置が違うだけで、全員同じペースで走ります。これが初期位相の意味です!
📊 初期位相θの3パターン
| 初期位相θ | 式の形 | 意味 |
|---|---|---|
| θ = 0° | v = Vmsinωt | 基準の波 (t=0のとき v=0) |
| θ = +60° | v = Vmsin(ωt+60°) | 60°先行している |
| θ = -60° | v = Vmsin(ωt-60°) | 60°遅れている |
🔑 ここが重要!
θ = +〇〇° → 波が左にシフト(進んでいる)
θ = -〇〇° → 波が右にシフト(遅れている)
符号に注意!プラスなのに「進む」、マイナスなのに「遅れる」という逆説的な関係です。
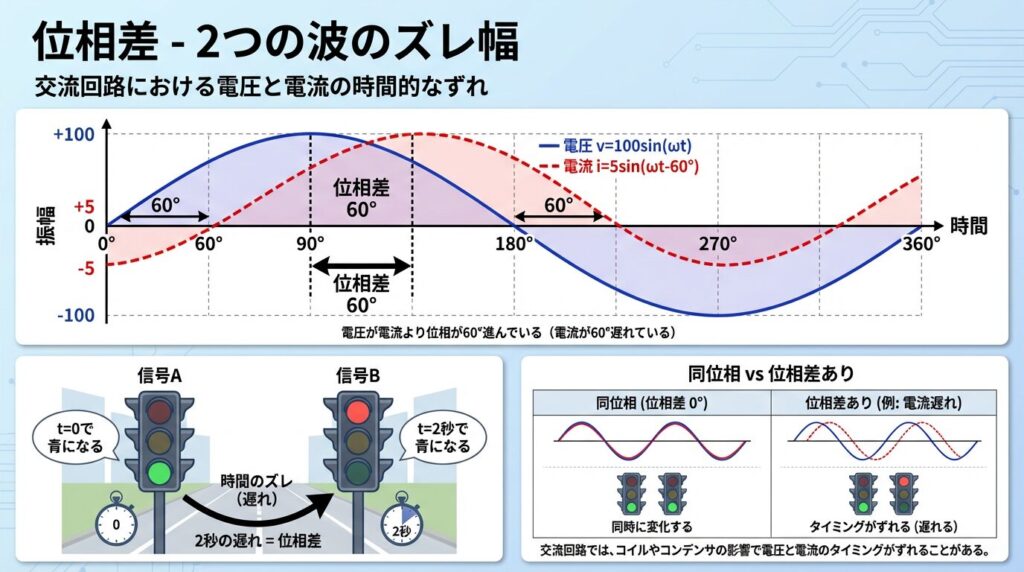
🔀 位相差(いそうさ)とは?| 2つの波のズレ
実際の回路では、電圧と電流が同時に動かないことがあります。 このズレを表すのが位相差です。
📌 位相差の定義
2つの波のスタート位置のズレ(角度)のこと
位相差 = θ₁ - θ₂
🚦 信号機の例えで理解
🚦 交差点の2つの信号機
東西の信号と南北の信号がズレて点滅しているイメージです。
- 東西の信号: 0秒で青に変わる
- 南北の信号: 30秒遅れて青に変わる
- この30秒のズレ = 位相差
📐 位相差の3つのパターン
| 関係 | 位相差 | 意味 |
|---|---|---|
| 電流が進む | +60° | 電流が電圧より先に最大値 |
| 電流が遅れる | -60° | 電流が電圧より後に最大値 |
| 同相 | 0° | 電圧と電流が同時に動く |
🧮 位相差の計算例
📝 計算例題
電圧: v = 100 sin ωt
電流: i = 5 sin (ωt - 60°)
問: 電流と電圧の位相差は?
電圧の初期位相: θv = 0°
電流の初期位相: θi = -60°
位相差 = θi - θv
位相差 = (-60°) - 0°
位相差 = -60°
✅ 答え: 電流は電圧より60°遅れている
📚 まとめ|交流の式を完全マスター!
✅ この記事で学んだこと
- 瞬時値 v: 時々刻々と変わる「今この瞬間」の電圧
- v = Vmsinωt: 交流の全ての動きを表す魔法の式
- 初期位相θ: 波のスタート位置のズレ(角度)
- 位相差: 2つの波(電圧と電流)のタイミングのズレ
- コイル/コンデンサ/抵抗: それぞれ特有の位相差を持つ
⚡ 電験三種の頻出パターン
- コイル(L) → 電流が電圧より90°遅れる
- コンデンサ(C) → 電流が電圧より90°進む
- 抵抗(R) → 電流と電圧が同相(0°)
この関係を覚えておくと、回路問題が一気に解きやすくなりますよ!
💡 実務で役立つポイント
🔌 現場での活用例
- オシロスコープで波形を見るとき → 瞬時値の変化が目で確認できます
- 力率改善を考えるとき → 位相差を意識することが重要です
- 共振回路を設計するとき → 位相が重要な役割を果たします
🎯 次に学ぶべきこと
📖 Step 1: 複素数表示
sin, cosではなくj(虚数単位)を使った表現方法を学びましょう。 計算がもっと楽になりますよ!
📖 Step 2: インピーダンス
抵抗だけでなく、コイルやコンデンサの「抵抗のようなもの」を理解しましょう。
📖 Step 3: 交流回路の計算
実際の回路で電圧・電流・電力を計算する方法を習得しましょう。
🔥 合格への最短ルート
📝 練習問題を解こう!
この記事の内容を理解したら、過去問で実践してみてください。
特に「瞬時値の計算」「位相差の判定」は頻出問題です。
✅ 推奨: 過去10年分の「交流回路」問題を3周解く
✅ 目標: 1問3分以内で解けるスピード感を身につける
🎉 あなたなら必ず合格できます!
交流の式は最初は難しく感じますが、
「ブランコ」「観覧車」「マラソン」のイメージで考えれば必ず理解できます。
焦らず、一歩ずつ進んでいきましょう!
📌 関連記事
最後まで読んでいただき、ありがとうございました!
この記事が少しでもお役に立てば幸いです。
💬 質問や感想があれば、コメント欄でお待ちしています!
