「コイルとコンデンサで、なぜ電流と電圧にズレが生じるんだろう…?」「抵抗だけ同相って、どういうこと?」
そんな疑問を抱えているあなたへ。電験三種の理論分野で最も重要なテーマの一つ、R-L-C素子の交流特性を、今日こそ完璧にマスターしましょう。
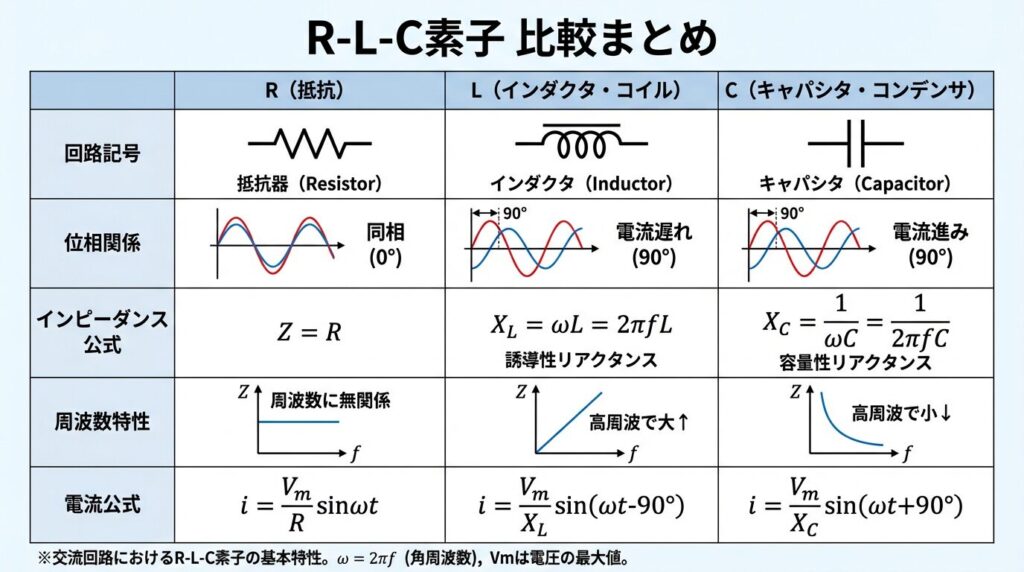
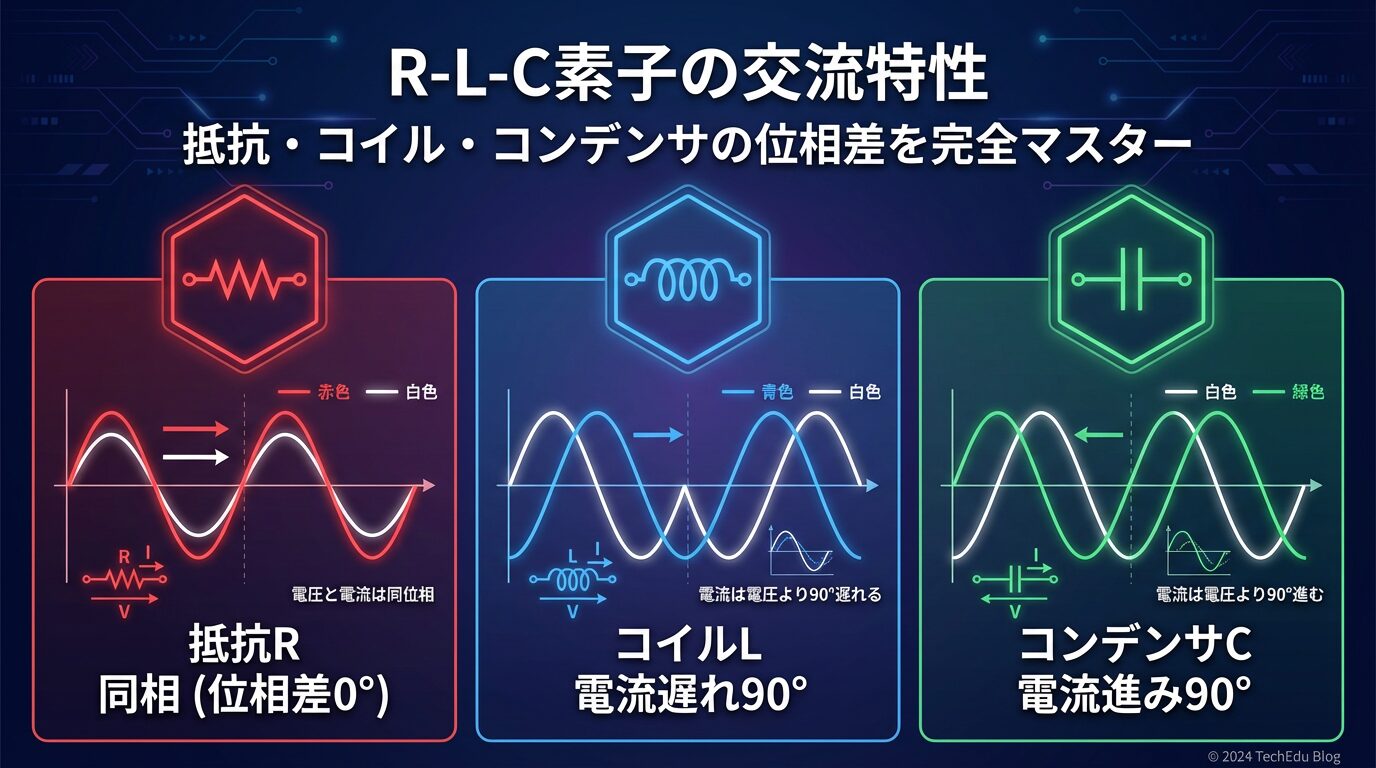
結論から言うと、抵抗Rは電圧と電流が同相、コイルLは電流が90°遅れ、コンデンサCは電流が90°進みます。この違いは、それぞれの素子が持つ物理的な性質によるものなんです。
- 抵抗Rでは電圧と電流が「同じタイミング」で変化する理由
- コイルLで電流が「遅れる」メカニズムを身近な例で理解
- コンデンサCで電流が「進む」理由を図解で完全マスター
- 3つの素子の違いを一目で理解できる比較表
この記事では、難しい数式は最小限に、「イメージ重視」で解説していきます。中学生でも理解できるよう、身近な例えや図解を豊富に使って説明しますので、安心してついてきてくださいね。
目次
交流回路とR-L-C素子の基本
まず前提として、交流回路では電圧と電流が時間とともに変化します。これを表すのが、あの有名な正弦波の式「v = Vmsinωt」ですね。
直流回路では、電圧をかければすぐに一定の電流が流れますが、交流回路では話が違います。R-L-C素子それぞれが、電圧の変化に対してどう「反応」するかが異なるんです。
この「反応の違い」こそが、位相差を生み出します。電圧と電流のタイミングがズレる現象ですね。
それでは、3つの素子を1つずつ、じっくり見ていきましょう!
抵抗R:電圧と電流が同相(位相差0°)
抵抗の交流特性 - オームの法則がそのまま使える!
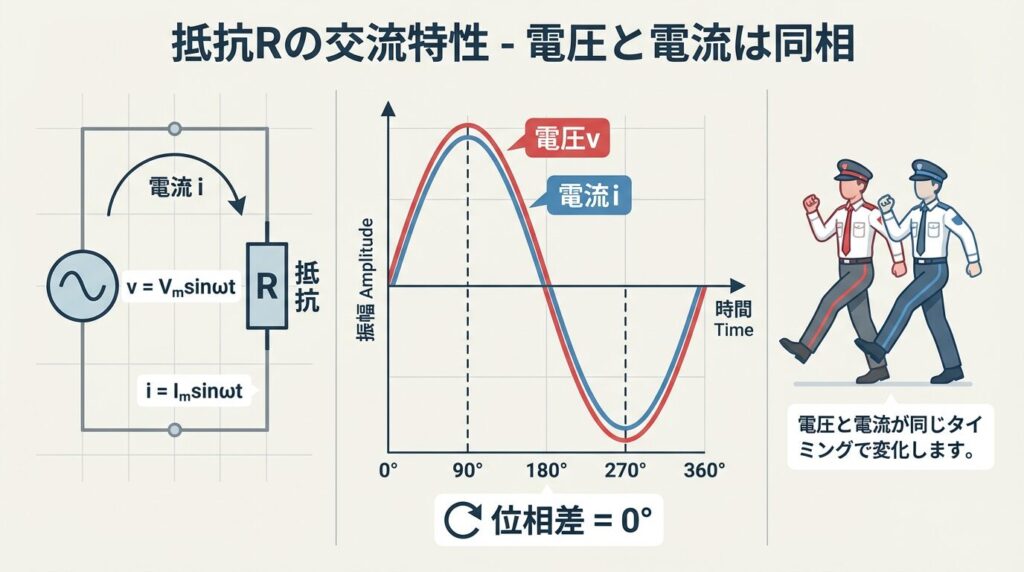
抵抗は、交流回路でも直流回路と同じように振る舞う、非常にシンプルな素子です。結論から言うと、抵抗では電圧と電流に位相差がありません(同相)。
これは、抵抗が電気エネルギーを熱に変換するだけで、電流の流れを時間的に遅らせたり進めたりする性質を持たないからです。
v = Vmsinωt のとき、i = (Vm/R)sinωt
→ 位相差 θ = 0°(同相)
身近な例で理解:息ピッタリのダンスペア
抵抗の動作を理解するには、ダンスペアの例えが分かりやすいです。
電圧が「リーダー役」で、電流が「フォロワー役」だと考えてください。抵抗の場合、フォロワーはリーダーの動きに一瞬で反応し、全く同じタイミングで動きます。リーダーが右に動けば、同時に右へ。左に動けば、同時に左へ。
これが「同相」の状態です。電圧の波と電流の波が、完全に重なり合っているんですね。
抵抗の重要ポイント
| 項目 | 特徴 |
|---|---|
| 位相差 | 0°(電圧と電流が同相) |
| インピーダンス | Z = R(純抵抗) |
| 周波数特性 | 周波数に無関係(常に一定) |
| エネルギー変換 | 電気→熱(消費) |
抵抗は交流でも直流でも同じように扱える、とてもシンプルな素子です。位相差ゼロ、これが抵抗の最大の特徴ですね!
コイルL:電流が90°遅れる
コイルの交流特性 - 電流の立ち上がりが遅い!
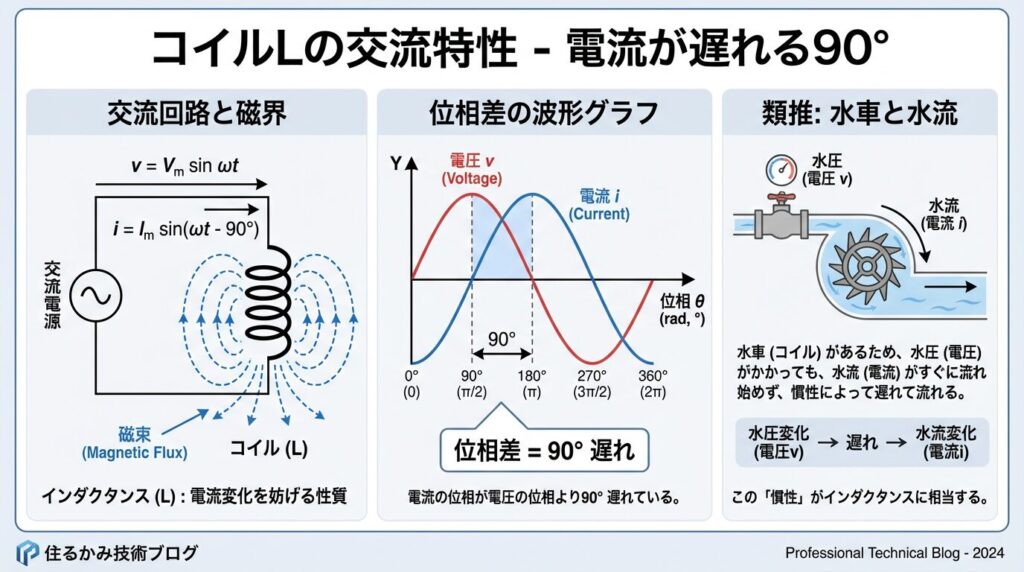
コイル(インダクタ)になると、話が少し複雑になります。結論から言うと、コイルでは電流が電圧より90°遅れます。
なぜこんなことが起こるのか? それは、コイルが持つ「電磁誘導」という性質のせいなんです。
v = Vmsinωt のとき、i = (Vm/XL)sin(ωt - 90°)
→ 位相差 θ = -90°(電流が遅れる)
XL = ωL = 2πfL (誘導リアクタンス)
身近な例で理解:重い水車を回す
コイルの動作は、重い水車を押して回そうとする場面をイメージするとわかりやすいです。
水車は重いので、あなたが押し始めても(電圧がかかっても)、すぐには回り始めません。水車が回り出す(電流が流れ始める)までには、少し時間がかかります。これが「遅れ」なんです。
さらに面白いのは、あなたが押すのをやめても(電圧がゼロになっても)、水車は慣性で回り続けます。これも電流が遅れる理由の1つです。
コイルで電流が遅れるメカニズム
コイルに電流を流そうとすると、コイル内部に磁界(磁場)が発生します。この磁界は、電流の変化を妨げる方向に働く「逆起電力」を発生させます。
これが「自己誘導作用」と呼ばれる現象です。電流を増やそうとすると、コイルが「ちょっと待って!」とブレーキをかけるんですね。
- 電圧が最大値のとき → 電流はまだゼロ(これから増える段階)
- 電圧がゼロになるとき → 電流が最大値(遅れて到達)
- 位相差はちょうど90°(1/4周期分のズレ)
【電験三種・理論】コイルとコンデンサの直列・並列 →
周波数が高いと抵抗が大きくなる
コイルのもう1つの特徴は、周波数が高くなるほど、電流が流れにくくなることです。
誘導リアクタンス XL = 2πfL という式を見ると分かりますが、周波数fが大きくなると、XLも大きくなります。つまり、コイルは高い周波数の信号をブロックする性質があるんです。
この性質を利用したのが「ローパスフィルタ」です。低い周波数だけを通して、高い周波数をカットする回路ですね。

コンデンサC:電流が90°進む
コンデンサの交流特性 - 電流がフライングスタート!
コンデンサは、コイルとは逆の性質を持ちます。結論から言うと、コンデンサでは電流が電圧より90°進みます。
これは、コンデンサが電荷を蓄える性質を持っているためです。電圧がゼロの時点でも、電流はすでに流れ始めているんですね。
v = Vmsinωt のとき、i = (Vm/XC)sin(ωt + 90°)
→ 位相差 θ = +90°(電流が進む)
XC = 1/(ωC) = 1/(2πfC) (容量リアクタンス)
身近な例で理解:バケツに水を注ぐ
コンデンサの動作は、空のバケツに水を注ぐ場面をイメージすると分かりやすいです。
バケツ(コンデンサ)が空っぽの状態では、水(電流)はどんどん流れ込みます。でも、バケツが満杯に近づくにつれて、水を注ぐ速度(電流)は遅くなっていきますよね。
つまり、電圧がまだゼロの時点(バケツが空の状態)で、電流は最大値になっています。電圧が最大になる頃(バケツが満杯)には、電流はゼロになります。これが「進み」の正体です。
コンデンサで電流が進むメカニズム
コンデンサの両極板には、電荷が蓄えられます。電圧の変化が速い(急激に変化する)ほど、電荷の出入りが激しくなり、大きな電流が流れます。
電圧v = Vmsinωtの変化速度(微分)は、dv/dt = ωVmcosωt = ωVmsin(ωt + 90°)となり、電圧より90°進んだ形になります。コンデンサに流れる電流は、この電圧の変化速度に比例するため、電流も90°進むんですね。
- 電圧がゼロのとき → 電流が最大値(電圧の変化が最も速い)
- 電圧が最大値のとき → 電流がゼロ(電圧の変化が止まる)
- 位相差はちょうど+90°(1/4周期分先行)
【電験三種・理論】コンデンサの直列・並列 →
周波数が高いと抵抗が小さくなる
コンデンサの面白い点は、周波数が高くなるほど、電流が流れやすくなることです。
容量リアクタンス XC = 1/(2πfC) という式を見ると、周波数fが大きくなると、XCは小さくなります。つまり、コンデンサは高い周波数の信号を通しやすい性質があります。
この性質を利用したのが「ハイパスフィルタ」です。高い周波数だけを通して、低い周波数をカットする回路ですね。コイルとは真逆の特性を持っています!