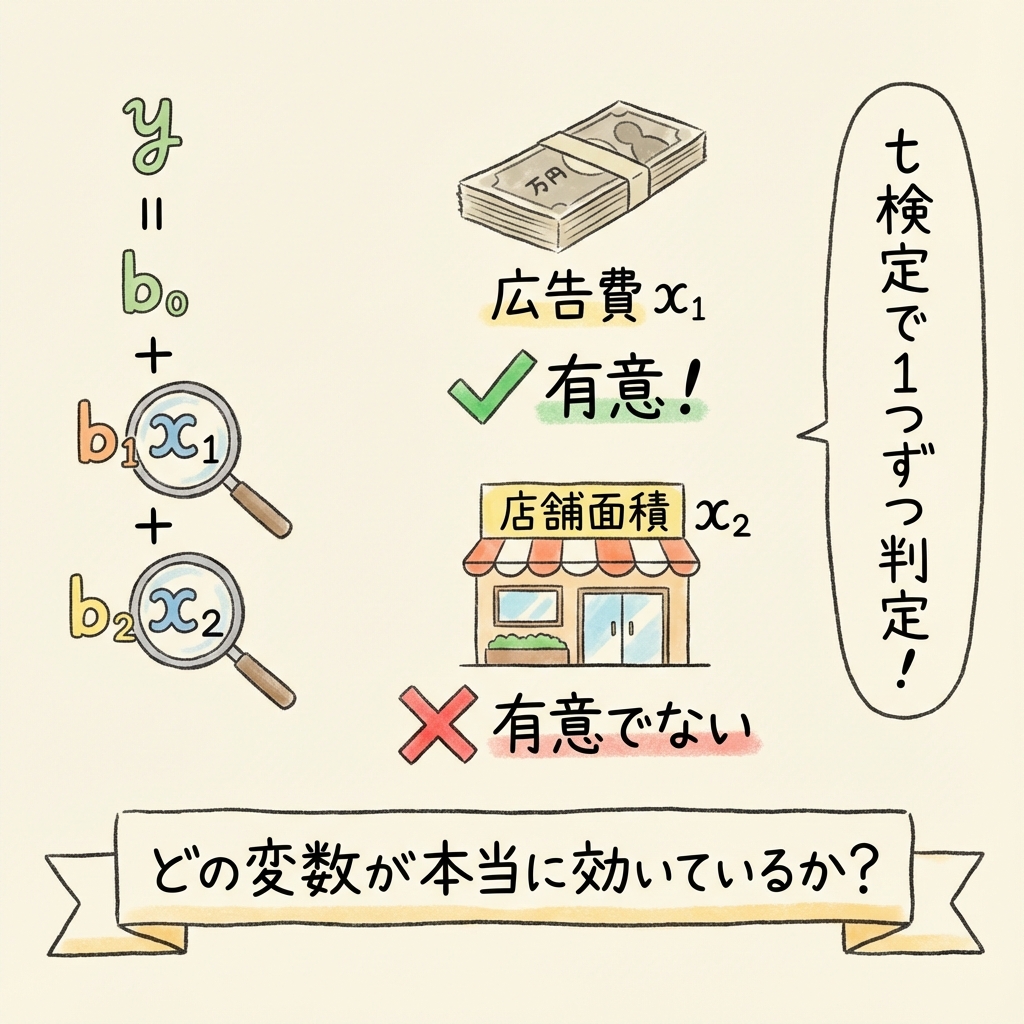
- 重回帰モデルは有意だったけど、どの変数が効いてるの?
- 偏回帰係数が大きい変数が「効いている」ってこと?
- t検定って何を検定してるの?計算方法は?
- 偏回帰係数のt検定が「何を判定しているのか」
- t値の計算方法を具体的な数値例で完全理解
- 「効いている変数」と「効いていない変数」の見分け方
「重回帰モデル全体は有意だった。でも、広告費と店舗面積、どっちが売上に効いてるの?」
この疑問、めちゃくちゃ重要です。
前回の記事で「モデル全体の有意性検定(F検定)」を学びましたね。あれは「少なくとも1つの変数は効いている」ことを証明するものでした。
でも、ビジネスで本当に知りたいのは「どの変数が効いているか」ですよね。
そこで登場するのが「偏回帰係数のt検定」です。
この検定を使えば、「広告費は売上に効いている!でも店舗面積は効いていない…」といったことが、統計的に証明できます。
この記事では、t検定の考え方から計算方法、判定基準まで、具体的な数値例を使って徹底解説します。
目次
偏回帰係数のt検定とは?
「個々の変数」が効いているかを1つずつ判定する
偏回帰係数のt検定とは、ひとことで言うと「各説明変数が、本当に目的変数に影響を与えているか?」を1つずつ判定する検定です。
F検定とt検定の違いを整理しておきましょう。
| 検定 | 判定内容 | イメージ |
|---|---|---|
| F検定 (前回) |
モデル全体が有意か? 「少なくとも1つの変数は効いているか?」 |
チーム全体の成績評価 |
| t検定 (今回) |
個々の変数が有意か? 「この変数は効いているか?」 |
選手1人ずつの成績評価 |
F検定:「このチームは強い?」(チーム全体の評価)
t検定:「この選手は活躍してる?」(選手1人ずつの評価)
チームが強くても、全員が活躍しているとは限りませんよね。
同じように、モデルが有意でも、すべての変数が効いているとは限りません。

帰無仮説と対立仮説を設定する
t検定でも、まず「帰無仮説」と「対立仮説」を設定します。
偏回帰係数のt検定では、変数ごとに次の仮説を検定します。
| 仮説 | 内容 |
|---|---|
| 帰無仮説 H₀ | βⱼ = 0 (この変数はyに影響を与えていない) |
| 対立仮説 H₁ | βⱼ ≠ 0 (この変数はyに影響を与えている) |
ここで βⱼ は「母集団における真の偏回帰係数」です。サンプルから計算した bⱼ とは区別してください。
「この変数の偏回帰係数が0である(効いていない)」と仮定したとき、
今回得られた bⱼ の値は「ありえないほど大きい」か?
もし「ありえないほど大きい」なら、「効いていない」という仮定は間違っている → つまり「この変数は効いている!」と結論できます。
t値の考え方|「係数の大きさ」を「バラつき」で割る
偏回帰係数の「信頼性」を測る
t検定の核心を理解しましょう。
「偏回帰係数 bⱼ が大きい = その変数は効いている」と思いがちですが、実はそう単純ではありません。
なぜなら、bⱼ の推定には「誤差」があるからです。
たとえば、広告費の偏回帰係数が b₁ = 5.0 だったとします。でも、別のサンプルで計算したら b₁ = 3.0 になるかもしれませんし、b₁ = 7.0 になるかもしれません。
この「バラつき」が大きいと、b₁ = 5.0 という値は「たまたま」かもしれないわけです。
体重計に乗って「60kg」と表示されたとします。
精度の高い体重計:何度測っても 59.8〜60.2kg → 60kgは信頼できる
精度の低い体重計:測るたびに 55〜65kg → 60kgは偶然かも…
偏回帰係数も同じ。「バラつき」が小さいほど信頼できます。
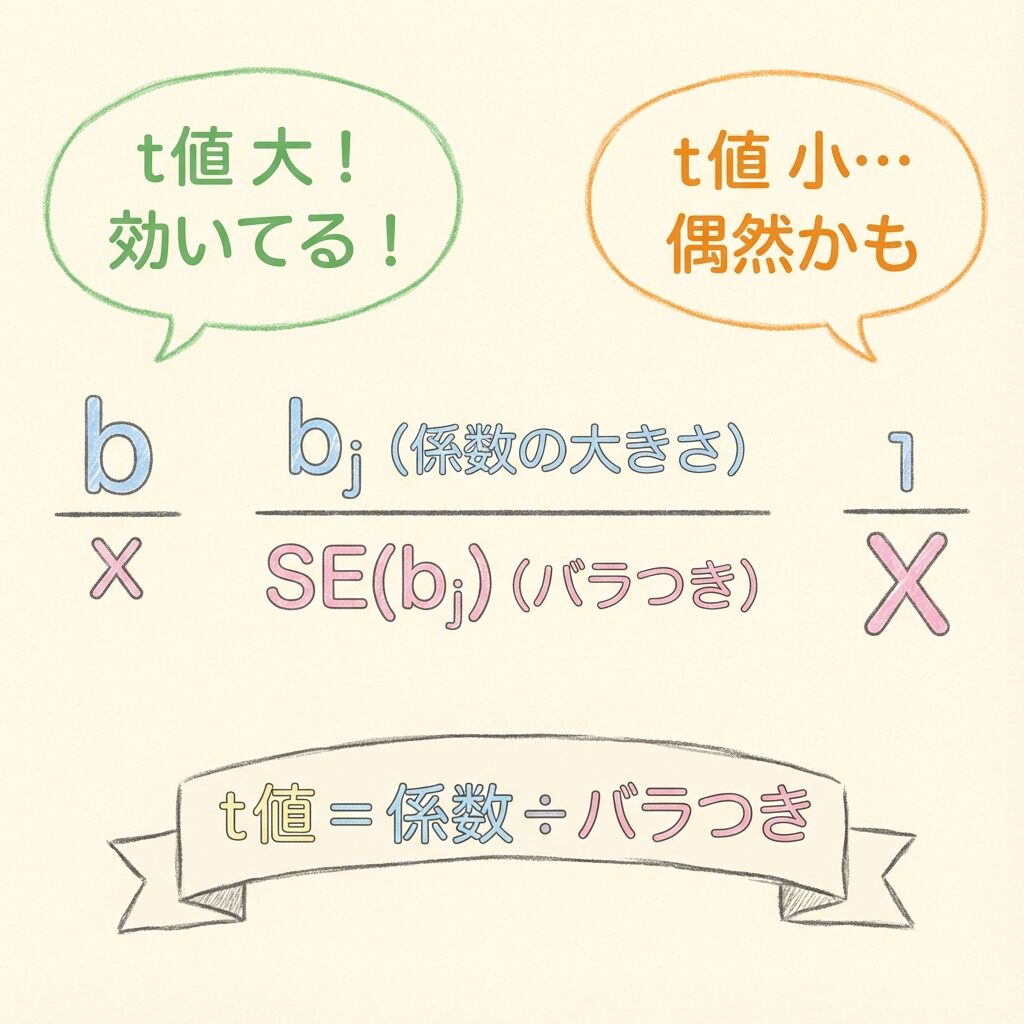
t値の公式
この「係数の大きさ」と「バラつき(標準誤差)」の比率がt値です。
bⱼ:偏回帰係数の推定値
SE(bⱼ):偏回帰係数の標準誤差
| t値の大きさ | 意味 |
|---|---|
| |t値|が大きい | 係数がバラつきに比べて大きい → 「偶然」とは考えにくい → 効いている! |
| |t値|が小さい | 係数がバラつきに比べて小さい → 「偶然」の可能性あり → 効いていないかも… |
t値はマイナスになることもあります(係数がマイナスの場合)。判定には絶対値 |t₀| を使います。
【計算例】t値を実際に求めてみよう
問題設定:売上を予測するモデル(前回の続き)
前回と同じ例を使います。売上(y)を「広告費(x₁)」と「店舗面積(x₂)」で予測するモデルです。
- サンプルサイズ:n = 15
- 説明変数の数:k = 2
- 残差の自由度:φe = n − k − 1 = 12
重回帰式:
ŷ = 10.0 + 5.0x₁ + 2.0x₂
| 変数 | 偏回帰係数 bⱼ | 標準誤差 SE(bⱼ) |
|---|---|---|
| 広告費 x₁ | 5.0 | 1.2 |
| 店舗面積 x₂ | 2.0 | 1.5 |
この情報から、各変数のt値を計算していきます。
ステップ1:広告費(x₁)のt値を計算
ステップ2:店舗面積(x₂)のt値を計算
2つのt値が計算できました。
| 変数 | 偏回帰係数 | 標準誤差 | t値 |
|---|---|---|---|
| 広告費 x₁ | 5.0 | 1.2 | 4.17 |
| 店舗面積 x₂ | 2.0 | 1.5 | 1.33 |
広告費は t = 4.17、店舗面積は t = 1.33。見るからに広告費の方が大きいですね。
でも、「大きい」かどうかは主観では決められません。t分布表と比較して判定します。

t分布表と比較して判定する
t分布表の見方
計算したt値が「大きい」かどうかを判定するには、t分布表を使います。
t分布表は、次の2つの情報で引きます。
- 有意水準α:通常は 0.05(5%)。両側検定なので α/2 = 0.025 で引く
- 自由度:残差の自由度 = 12
有意水準5%(両側)のt分布表を見ると、自由度12のとき:
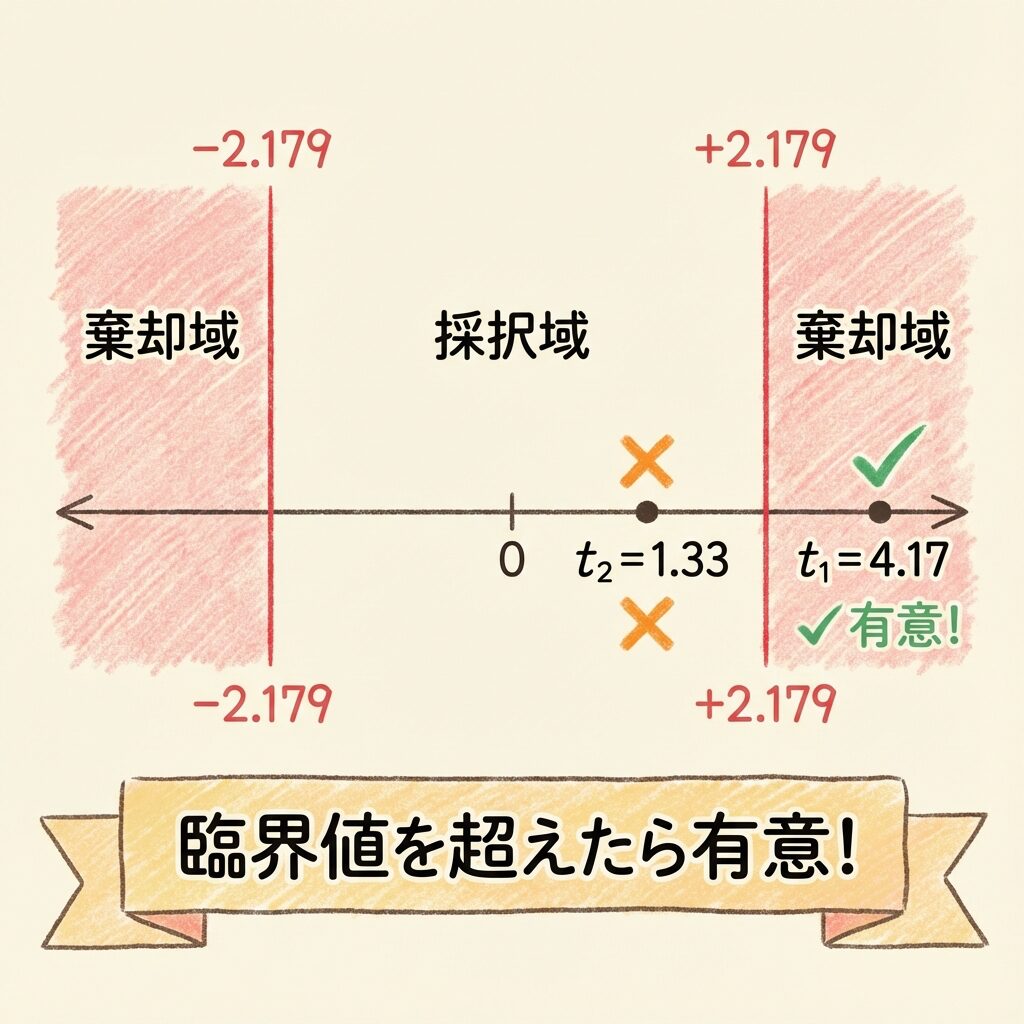
t(12, 0.025) = 2.179
判定:|t₀| > t表 なら「有意」
さあ、いよいよ各変数を判定しましょう。
広告費(x₁)の判定
| 比較対象 | 値 |
|---|---|
| 計算したt値 |t₁| | 4.17 |
| t表の値(臨界値) | 2.179 |
|t₁| = 4.17 > t表 = 2.179 なので…
広告費は売上に影響を与えていると言える
店舗面積(x₂)の判定
| 比較対象 | 値 |
|---|---|
| 計算したt値 |t₂| | 1.33 |
| t表の値(臨界値) | 2.179 |
|t₂| = 1.33 < t表 = 2.179 なので…
店舗面積が売上に影響を与えているとは言えない
結果のまとめ
| 変数 | t値 | t表 | 判定 |
|---|---|---|---|
| 広告費 x₁ | 4.17 | 2.179 | 有意 ✓ |
| 店舗面積 x₂ | 1.33 | 2.179 | 有意でない ✗ |
この結果から、売上を伸ばすには広告費を増やすのが効果的と言えます。
一方、店舗面積を広げても売上への効果は統計的に確認できませんでした。
もちろん、これは「このデータでは」という条件付きです。店舗面積が本当に関係ないとは限りません。
有意でない変数はどうする?
選択肢①:モデルから除外する
店舗面積のように「有意でない」と判定された変数は、モデルから除外することを検討できます。
有意でない変数を入れたままにすると…
- モデルが無駄に複雑になる
- 他の変数の効果がわかりにくくなる(多重共線性のリスク)
- 予測精度が下がる可能性がある
ただし、理論的に重要な変数は有意でなくても残すことがあります。専門知識と統計結果の両方を考慮して判断しましょう。
選択肢②:変数選択の手法を使う
変数が多い場合は、統計的な変数選択法を使うと便利です。
- ステップワイズ法:変数を1つずつ追加・削除しながら最適なモデルを探す
- AIC(赤池情報量基準):モデルの「良さ」と「複雑さ」のバランスで選ぶ
- 増加法・減少法:変数を追加していく/削除していく方法
「有意でない」は「効果がないと証明された」ではありません。
正確には「効果があるとは言えなかった」です。
サンプルサイズが小さいと、本当は効果があっても有意にならないことがあります。
F検定とt検定の関係を整理
両方やる意味は?
「F検定もt検定も両方やる必要あるの?」と思うかもしれません。
答えは「Yes」です。両者は役割が違います。
| 検定 | 質問 | 答え |
|---|---|---|
| F検定 | このモデルは使えるか? | 有意 → 少なくとも1つは効いてる |
| t検定 | どの変数が効いてるか? | 各変数を1つずつ判定 |
Step 1:F検定でモデル全体をチェック → 有意ならStep 2へ
Step 2:t検定で各変数をチェック → どの変数が効いているか特定
Step 3:有意でない変数の除外を検討 → モデルを改善
まとめ
この記事では、偏回帰係数のt検定について解説しました。
- t検定は「各変数が効いているか」を1つずつ判定する
- t値 = 偏回帰係数 ÷ 標準誤差
- |t₀| > t表 なら「有意」→ その変数は効いている
- 有意でない変数は、モデルから除外を検討する
- F検定(全体)とt検定(個別)は両方やることが大切
t検定で「効いている」とわかった変数について、次は「どのくらい効いているか」の信頼区間を求めましょう。
📚 次に読むべき記事
偏回帰係数がどの範囲にあるか、区間で推定する方法
モデル全体の有意性検定を復習したい方へ
偏回帰係数の意味を直感的に理解したい方へ