💭 こんな疑問、ありませんか?
- 「ワイブル分布って、正規分布や指数分布と何が違うの?」
- 「形状パラメータmって、結局何を表してるの?」
- 「故障率曲線(バスタブカーブ)との関係がわからない」
✅ この記事でわかること
- ワイブル分布とは何か、なぜ信頼性工学で使われるのか
- 形状パラメータmの意味=故障パターン(初期・偶発・摩耗)を決める
- 尺度パラメータηの意味=寿命の長さを決める
- 信頼度関数R(t)と故障率関数λ(t)の導出
- バスタブカーブとの関係をイメージで理解
📌 結論(3秒で理解)
ワイブル分布は、形状パラメータmの値を変えるだけで、
「初期故障」「偶発故障」「摩耗故障」のすべての故障パターンを表現できる万能分布です。
信頼性工学では「故障データの分析」に欠かせないツールです。
製品の寿命を予測したい。故障のパターンを数値で把握したい。
そんなとき、信頼性工学で最もよく使われるのがワイブル分布です。
「分布」と聞くと難しそうですが、ワイブル分布の本質はたった2つの数字で故障の特徴を表現できることです。
この記事では、ワイブル分布を図解たっぷり・中学生でもわかる言葉で解説します。
「mが大きいと何が変わるのか?」「ηは何を意味するのか?」
イメージで理解すれば、怖くありません。
目次
🎯 ワイブル分布とは?
📖 ワイブル分布の定義
スウェーデンの数学者ワロディ・ワイブルが1951年に提唱した確率分布。
2つのパラメータを調整するだけで、さまざまな故障パターンを表現できる。
信頼性工学では「最も使われる分布」と言っても過言ではありません。
💡 なぜワイブル分布が使われるのか?
世の中には「正規分布」「指数分布」などいろいろな分布がありますが、
故障の分析にはワイブル分布が圧倒的に便利です。その理由は…
🏆 ワイブル分布が選ばれる3つの理由
- 柔軟性:パラメータを変えるだけで、あらゆる故障パターンを表現できる
- 物理的意味:パラメータが「故障の性質」に直結していて解釈しやすい
- 実績:機械・電子部品・材料など、幅広い分野で有効性が実証されている
📐 ワイブル分布の2つのパラメータ
ワイブル分布は、たった2つの数字で形が決まります。
① 形状パラメータ m
故障のパターン(形)を決める
別名:ワイブル係数、形状母数
記号:m または β(ベータ)
② 尺度パラメータ η
寿命の長さ(スケール)を決める
別名:特性寿命、尺度母数
記号:η(イータ)または α(アルファ)
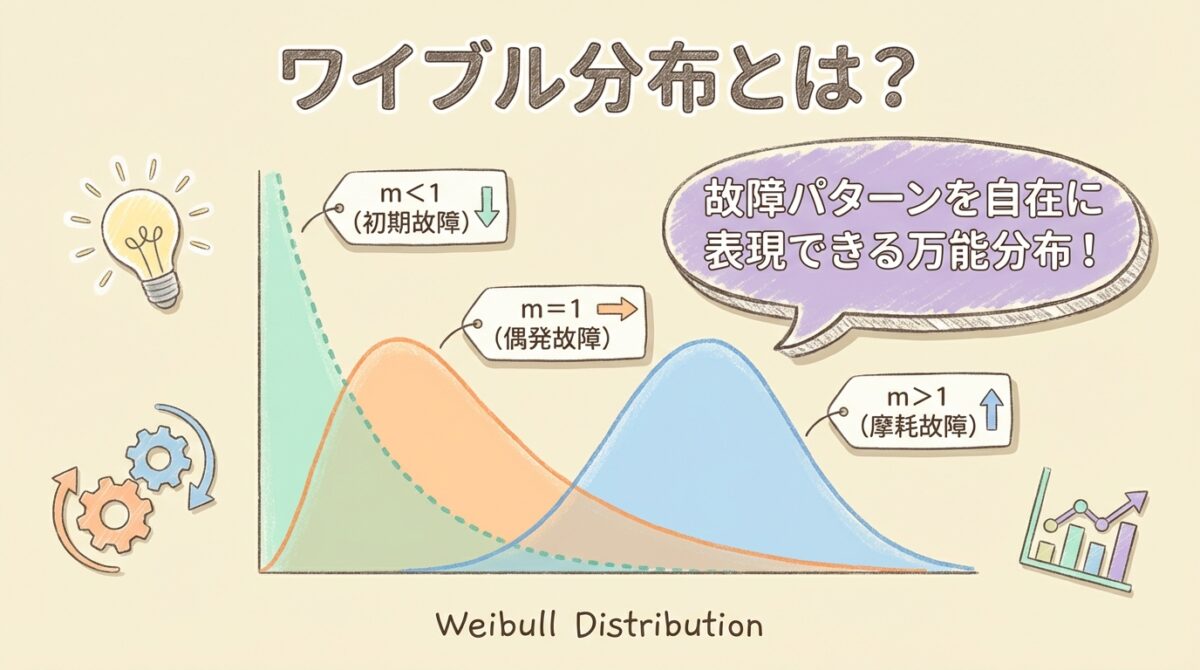
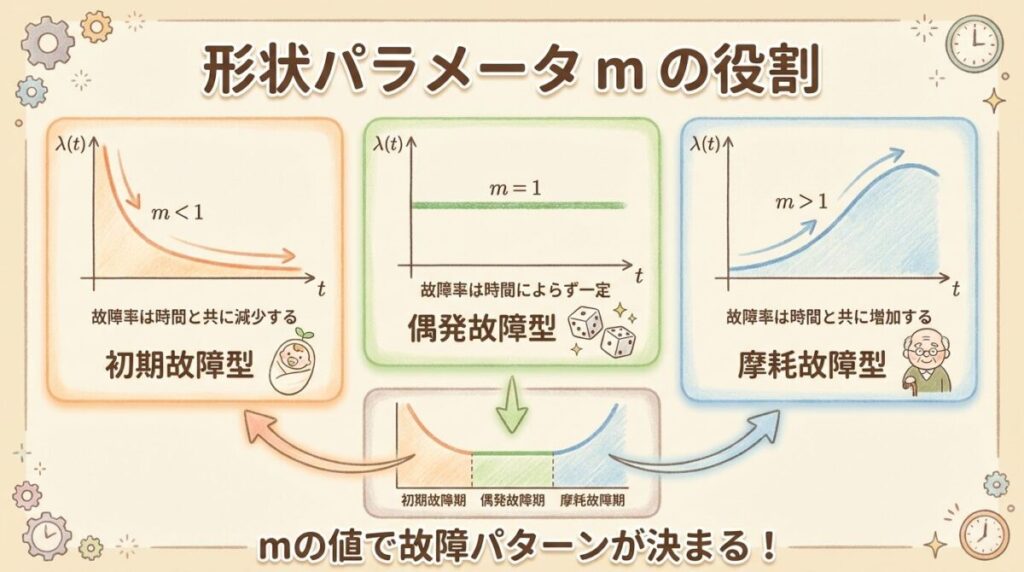
🔴 形状パラメータ m ─ 故障パターンを決める
形状パラメータmは、「この製品がどんな壊れ方をするか」を決めます。
mの値によって、故障率の「形」が劇的に変わります。
📊 mの値と故障パターンの関係
| mの値 | 故障率の傾向 | 故障パターン | バスタブカーブ |
|---|---|---|---|
| m < 1 | 時間とともに減少 | 初期故障型(DFR) | 左側の下り坂 |
| m = 1 | 一定(指数分布) | 偶発故障型(CFR) | 真ん中の平ら |
| m > 1 | 時間とともに増加 | 摩耗故障型(IFR) | 右側の上り坂 |
🎭 mの値を「人間の一生」でイメージする
💡 人間の死亡率で考えると…
m < 1(初期故障型):生まれたばかりの赤ちゃん
→ 最初は弱いが、生き延びるほど丈夫になる
m = 1(偶発故障型):若い成人
→ 事故など、いつ起きるかわからないランダムな死亡
m > 1(摩耗故障型):高齢者
→ 年を取るほど、死亡率が上がっていく
🏭 実際の製品での例
- m ≈ 0.5〜0.8:半導体の初期不良、溶接の欠陥
- m ≈ 1.0:電子部品のランダム故障
- m ≈ 2.0〜3.0:ベアリング、歯車などの機械部品の摩耗
- m ≈ 3.5:金属疲労による破壊
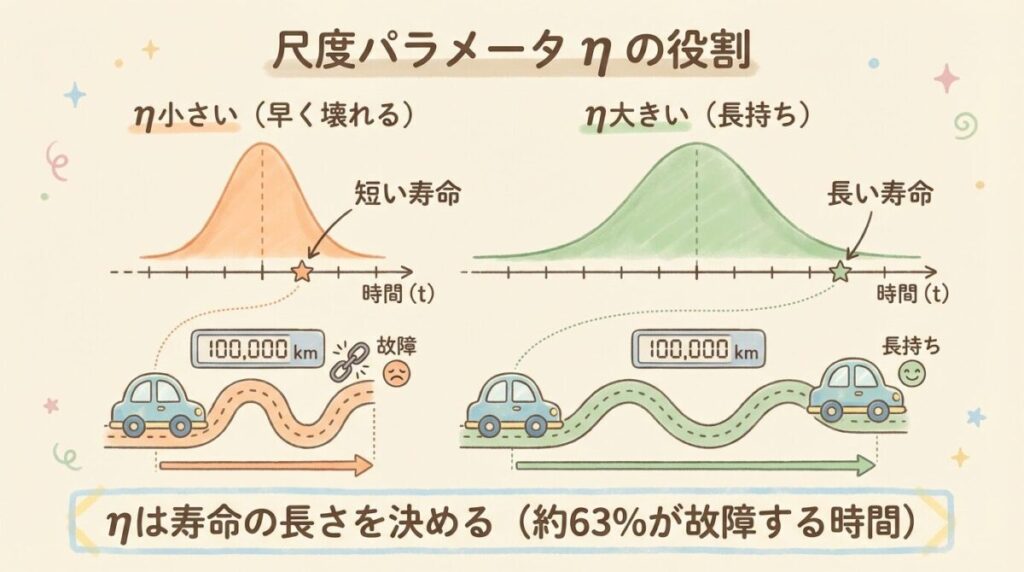
🟢 尺度パラメータ η ─ 寿命の長さを決める
尺度パラメータη(イータ)は、「この製品がどのくらい長持ちするか」を決めます。
mが「形」なら、ηは「大きさ」を決めるパラメータです。
📖 尺度パラメータηの意味
全体の約63.2%が故障するまでの時間を表します。
別名:特性寿命(characteristic life)
単位:時間、回数、走行距離など(製品に応じて)
🚗 車の走行距離でイメージする
💡 同じ形状パラメータ、違う尺度パラメータ
2種類のタイヤがあるとします。どちらも同じ摩耗パターン(m=2)ですが…
タイヤA:η = 30,000km
→ 約63%のタイヤが30,000kmまでに交換が必要
タイヤB:η = 50,000km
→ 約63%のタイヤが50,000kmまでに交換が必要
ηが大きいほど「長持ち」ということです。
🤔 なぜ「63.2%」という中途半端な数字?
📐 数学的な理由
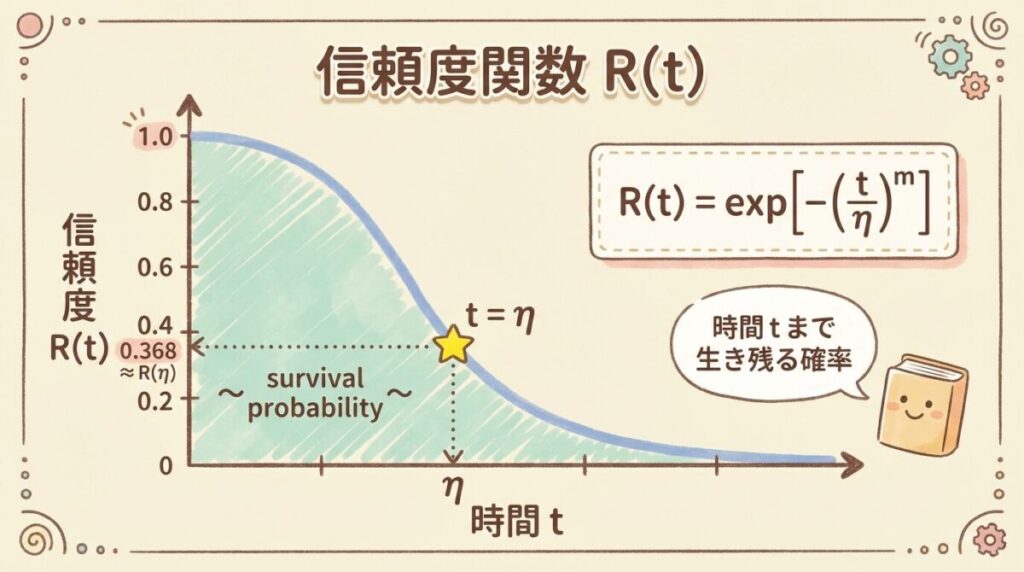
信頼度関数 R(t) = exp[−(t/η)m] において、
t = η を代入すると…
R(η) = exp[−1] = 1/e ≈ 0.368
つまり、t = η のとき約36.8%が生存している。
逆に言えば、約63.2%が故障済みということです。
この「1/e」という値は、数学的に扱いやすいため基準として使われます。
🔵 ワイブル分布の4つの関数
ワイブル分布には、用途に応じた4つの関数があります。
それぞれの意味と関係を押さえましょう。
📐 4つの関数と公式
① 信頼度関数 R(t)
R(t) = exp[−(t/η)m]
意味:時間tまで故障せずに生き残る確率
② 累積故障分布関数 F(t)
F(t) = 1 − R(t) = 1 − exp[−(t/η)m]
意味:時間tまでに故障する確率(信頼度の裏返し)
③ 確率密度関数 f(t)
f(t) = (m/η)(t/η)m−1 exp[−(t/η)m]
意味:時間tで故障する確率の密度(グラフの「高さ」)
④ 故障率関数 λ(t)
λ(t) = f(t)/R(t) = (m/η)(t/η)m−1
意味:時間tまで生き残った製品が、次の瞬間に故障する確率
🔗 4つの関数の関係
R(t) + F(t) = 1 (生存 + 故障 = 100%)
f(t) = F(t)の微分 = −R(t)の微分
λ(t) = f(t) / R(t) (瞬間故障率)
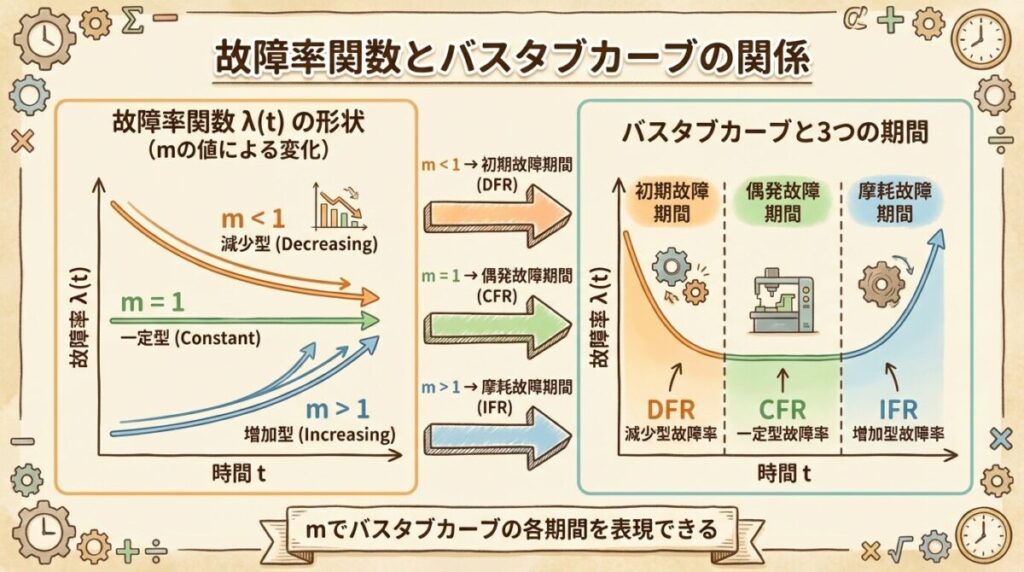
🟠 故障率関数とバスタブカーブの関係
ワイブル分布の最大の強みは、形状パラメータmを変えるだけで、バスタブカーブの3つの期間すべてを表現できることです。
🛁 バスタブカーブとの対応
m < 1
故障率:減少型(DFR)
バスタブ左側
初期故障期間
m = 1
故障率:一定型(CFR)
バスタブ底面
偶発故障期間
m > 1
故障率:増加型(IFR)
バスタブ右側
摩耗故障期間
※ DFR = Decreasing Failure Rate、CFR = Constant Failure Rate、IFR = Increasing Failure Rate
📐 故障率関数の計算例
📝 例題
ある部品の故障データを分析したところ、以下のパラメータが得られた。
m = 2、η = 1000時間
t = 500時間 における故障率 λ(500) を求めなさい。
📊 計算プロセス
Step 1:故障率関数の公式を確認
λ(t) = (m/η)(t/η)m−1
Step 2:数値を代入
λ(500) = (2/1000)(500/1000)2−1
λ(500) = 0.002 × (0.5)1
Step 3:計算して完了!
λ(500) = 0.001 [/時間] = 0.1%/時間
💡 結果の解釈
m = 2 > 1 なので、これは摩耗故障型の部品です。
t = 500時間の時点で、1時間あたり約0.1%の確率で故障します。
m > 1なので、時間が経つほどこの値は大きくなっていきます(摩耗が進むため)。
🎯 m = 1 のとき、指数分布になる
💡 ワイブル分布と指数分布の関係
m = 1 を代入すると、故障率関数は…
λ(t) = (1/η)(t/η)0 = 1/η = 一定
これは「故障率が一定」という指数分布の特徴そのものです。
つまり、指数分布はワイブル分布の特殊ケース(m=1)なのです。
📝 まとめ
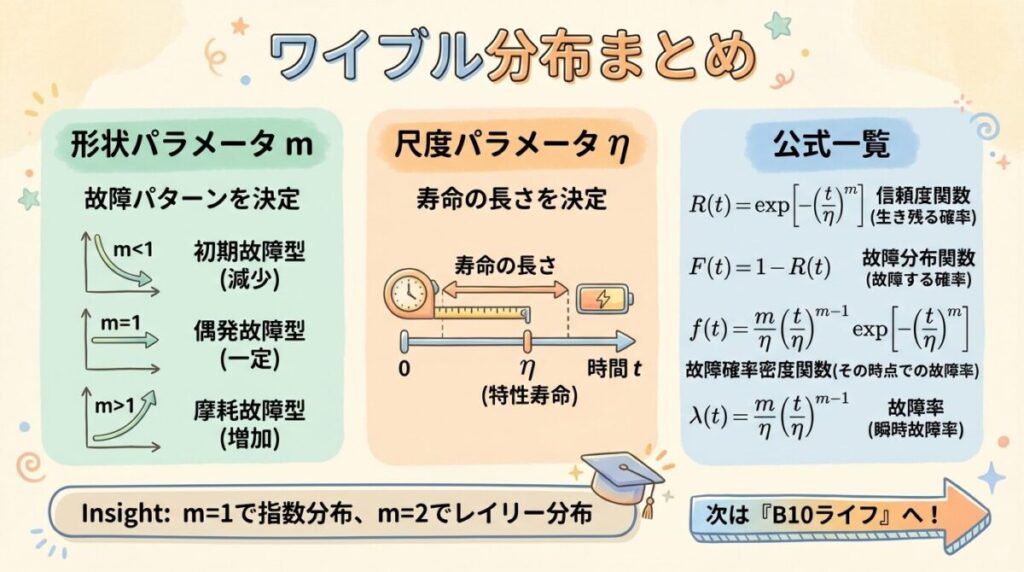
✅ この記事のポイント
- ワイブル分布は、2つのパラメータであらゆる故障パターンを表現できる万能分布
-
形状パラメータ m:故障の「パターン」を決める
m < 1(初期故障)、m = 1(偶発故障)、m > 1(摩耗故障) -
尺度パラメータ η:寿命の「長さ」を決める
約63.2%が故障するまでの時間(特性寿命) - 4つの関数:R(t)信頼度、F(t)累積故障、f(t)確率密度、λ(t)故障率
- 指数分布はm=1のワイブル分布(特殊ケース)
🔑 覚えておくべき公式
信頼度関数
R(t) = e−(t/η)m
故障率関数
λ(t) = (m/η)(t/η)m−1
ポイント:t = η のとき、R(η) = 1/e ≈ 0.368(約36.8%が生存)
💡 形状パラメータ m の早見表
| mの値 | 故障率 | 故障タイプ |
|---|---|---|
| m < 1 | 減少(DFR) | 初期故障 |
| m = 1 | 一定(CFR) | 偶発故障 |
| m > 1 | 増加(IFR) | 摩耗故障 |
🚀 次に読むべき記事
ワイブル分布を理解できたら、次は「B10ライフ」を学びましょう。
「10%が故障するまでの時間」という実務で超重要な指標です。
📖 NEXT STEP
【図解】B10ライフとは?|"10%が壊れる時間"でベアリングの寿命を予測する
ベアリングや機械部品の寿命予測に使われる「B10ライフ」の意味と計算方法を図解。ワイブル分布との関係も解説します。
📚 関連記事
【超入門】信頼性工学とは?|製品が"壊れない"を数値化する技術を完全図解 信頼性指標
【図解】MTBFとMTTFの違い|"修理できるか"で使い分ける2つの指標 故障率曲線
【完全図解】故障率曲線(バスタブカーブ)|製品の"寿命"を3つの期間で理解する システム信頼性
【完全図解】信頼性ブロック図の作り方|直列系・並列系・冗長系をマスター
📖 信頼性工学シリーズ
- 信頼性工学とは?
- MTBFとMTTFの違い
- 故障率曲線(バスタブカーブ)
- アベイラビリティ(可用性)
- 信頼性ブロック図
- ワイブル分布 ← 今ここ
- B10ライフ ← 次はこれ!
- 打ち切りデータ
- ワイブル確率紙(準備中)
💡 ワイブル分布は、「mを見ればどんな壊れ方をする製品かわかる」という強力なツールです。
故障データを分析するときは、まず「mがいくつか?」を確認しましょう!
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。