💭 こんな疑問、ありませんか?
- 「B10ライフって、カタログでよく見るけど何のこと?」
- 「なぜ『10%』という数字が使われるの?」
- 「ワイブル分布のηとB10って、どう違うの?」
✅ この記事でわかること
- B10ライフとは何か=「10%が故障するまでの時間」
- Bxライフの考え方=xを変えればいろんな寿命が分かる
- なぜ「10%」が業界標準として使われるのか
- ワイブル分布からB10を計算する方法
- 実務での寿命予測・保全計画への活用法
📌 結論(3秒で理解)
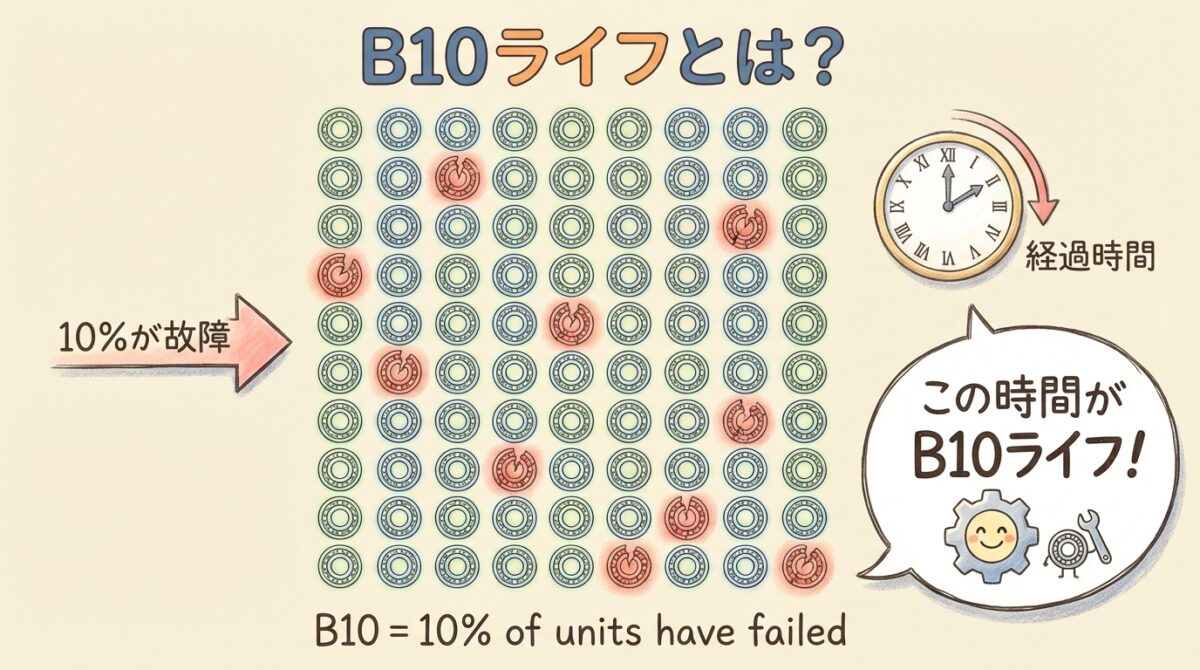
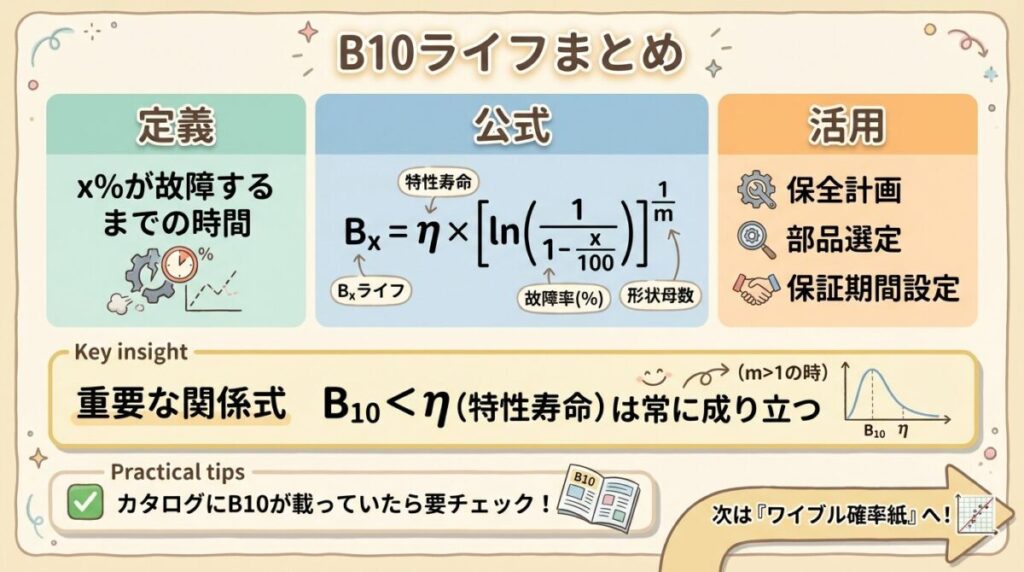
B10ライフとは、「全体の10%が故障するまでの時間」のこと。
ベアリングなどの機械部品では、この値を基準に交換時期や保証期間を決めます。
「90%はまだ使える」という安全マージンを持った寿命指標です。
ベアリング、歯車、モーター。
機械部品のカタログを見ると、「B10寿命:○○時間」という表記をよく見かけます。
この「B10」、なんとなくスルーしていませんか?
実は、これを理解すると「いつ部品を交換すべきか」が数字で判断できるようになります。
この記事では、B10ライフの意味と計算方法を図解たっぷり・中学生でもわかる言葉で解説します。
目次
🎯 B10ライフとは?
📖 B10ライフの定義
同じ条件で使用した製品のうち、全体の10%が故障するまでの時間(または回数)。
別の言い方をすると、「90%がまだ生き残っている時間」のこと。
記号:B10 または L10(Lはlife:寿命の意味)
🎱 100個のボールで考える
💡 イメージで理解しよう
100個の同じベアリングを同時に動かし始めたとします。
しばらくすると、1個、2個…と故障していきます。
そして、10個目が故障した瞬間の時間。
これがB10ライフです。
この時点で、90個(90%)はまだ動いている状態です。
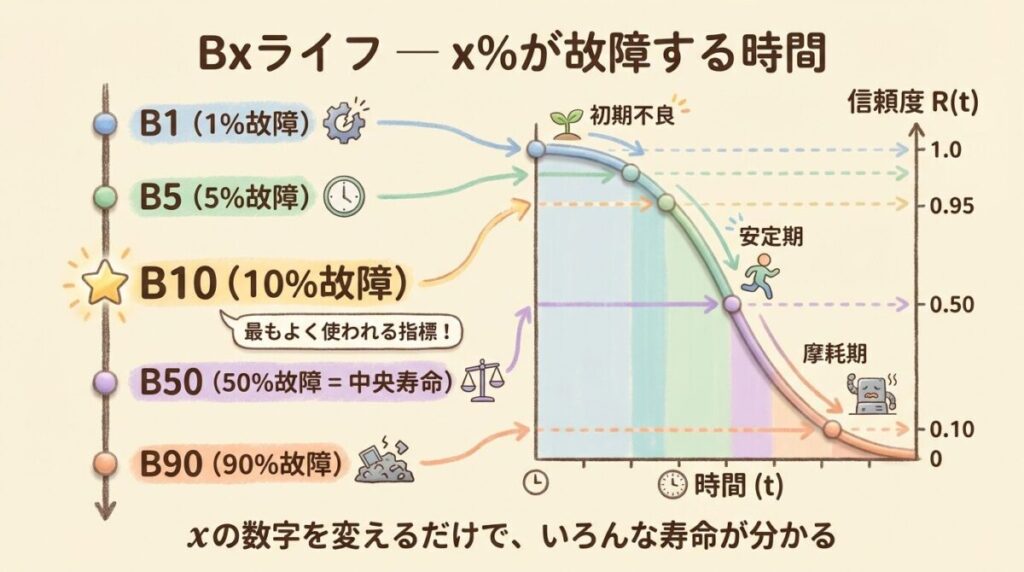
🟢 Bxライフ ─ xを変えればいろんな寿命が分かる
B10の「10」は「10%」を意味します。
この数字を変えれば、いろいろな寿命を表現できます。
| 記号 | 意味 | 用途・特徴 |
|---|---|---|
| B1 | 1%が故障する時間 | 超高信頼性が必要な場合(航空宇宙など) |
| B5 | 5%が故障する時間 | 安全性重視の製品 |
| B10 | 10%が故障する時間 | 最も一般的(業界標準) |
| B50 | 50%が故障する時間 | 中央寿命(メジアン寿命) |
| B90 | 90%が故障する時間 | ほとんどが寿命を迎える時間 |
🤔 なぜ「10%」が標準なのか?
B10が業界標準になった理由は、3つのバランスにあります。
🏆 B10が選ばれる3つの理由
-
実験で確認しやすい
1%故障を待つには大量のサンプルと長い時間が必要。10%なら現実的。 -
安全マージンがある
B10の時点で「90%はまだ使える」ので、交換時期の基準として安全。 -
歴史的に定着
1924年にスウェーデンのSKF社がベアリング寿命の指標として提唱。
📌 B10とη(特性寿命)の違い
ワイブル分布のη(イータ)は「約63.2%が故障する時間」でした。
一方、B10は「10%が故障する時間」。
つまり、B10 < η が常に成り立ちます。
B10のほうが「早い段階」の寿命を表しているのです。

🔴 B10ライフの計算方法
B10ライフは、ワイブル分布のパラメータ(m、η)から計算できます。
公式を導出してみましょう。
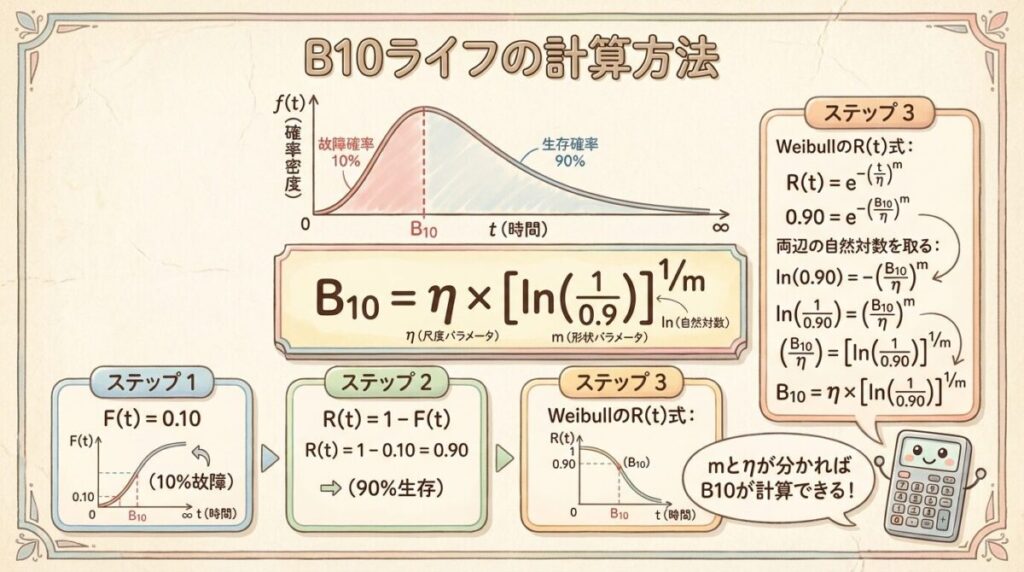
📐 公式の導出
Step 1:B10の定義を確認
B10とは「累積故障確率F(t)が10%になる時間」
つまり、F(B10) = 0.10、R(B10) = 0.90
Step 2:ワイブル分布の信頼度関数を使う
R(t) = exp[−(t/η)m]
R(B10) = 0.90 を代入すると…
0.90 = exp[−(B10/η)m]
Step 3:両辺の自然対数をとる
ln(0.90) = −(B10/η)m
−ln(0.90) = (B10/η)m
ln(1/0.90) = (B10/η)m
Step 4:B10について解く
B10/η = [ln(1/0.90)]1/m
B10 = η × [ln(1/0.90)]1/m
🔑 B10ライフの公式
B10 = η × [ln(1/0.90)]1/m
※ ln(1/0.90) ≈ 0.1054
📐 一般化:Bxライフの公式
「10%」を「x%」に一般化すると、以下の公式になります。
🔑 Bxライフの一般公式
Bx = η × [ln(1/(1−x/100))]1/m
x = 故障率(%)、例:x=10 なら B10
💡 よく使う ln(1/(1−x/100)) の値
| x(%) | ln(1/(1−x/100)) | 意味 |
|---|---|---|
| 1 | 0.01005 | B1 |
| 5 | 0.05129 | B5 |
| 10 | 0.10536 | B10(最もよく使う) |
| 50 | 0.69315 | B50(中央寿命) |
| 63.2 | 1.00000 | = η(特性寿命) |
🟠 計算例:B10ライフを求める
📝 例題
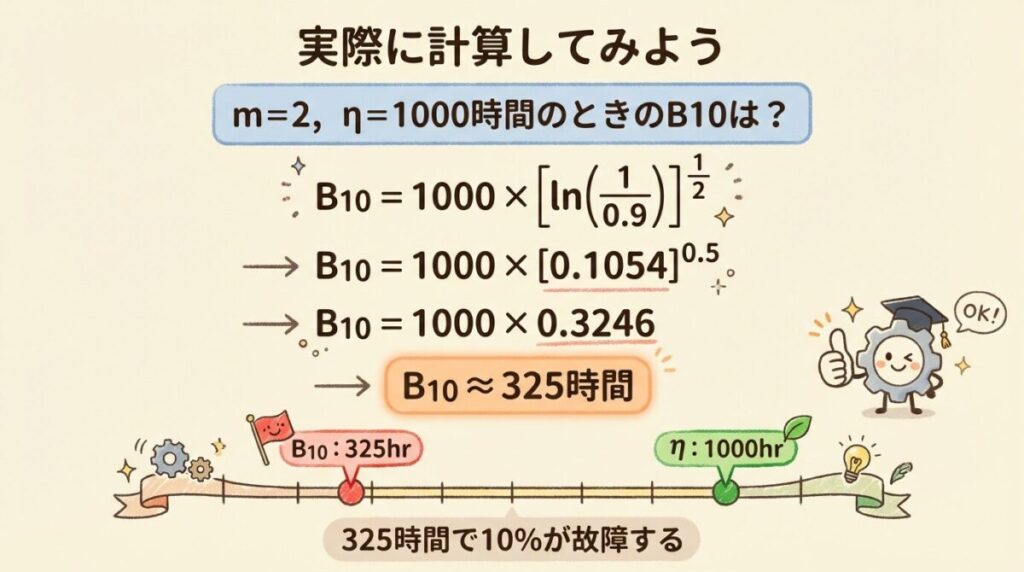
あるベアリングの故障データを分析したところ、以下のワイブルパラメータが得られた。
形状パラメータ m = 2
尺度パラメータ η = 10,000時間
このベアリングのB10ライフを求めなさい。
📊 計算プロセス
Step 1:公式を確認
B10 = η × [ln(1/0.90)]1/m
Step 2:ln(1/0.90) を計算
ln(1/0.90) = ln(1.111...) ≈ 0.1054
Step 3:1/m乗を計算
[0.1054]1/2 = [0.1054]0.5 = √0.1054 ≈ 0.3246
Step 4:ηを掛けて完了!
B10 = 10,000 × 0.3246 = 3,246時間
✅ 答え:B10 ≈ 3,246時間
約3,246時間で全体の10%が故障する(90%はまだ使える)
💡 結果の解釈
η = 10,000時間(約63%故障)に対して、
B10 = 3,246時間(10%故障)。
B10はηの約32%の位置にあります。
つまり、「特性寿命の約1/3の時点で10%が故障し始める」ということ。
保全計画では、3,000時間を超えたら点検・交換を検討するのが安全です。
🔵 実務でのB10ライフの活用
🏭 活用シーン①:保全計画の策定
「いつ部品を交換すべきか?」の判断基準として使えます。
例:B10 = 3,246時間 のベアリングの場合
→ 3,000時間を目安に予防交換を計画
→ 「90%はまだ使える」という安全マージンを確保
🏭 活用シーン②:部品の選定・比較
複数のメーカーの部品を比較するとき、B10ライフが長いほうが長寿命です。
| メーカー | B10ライフ | 価格 |
|---|---|---|
| A社 | 3,000時間 | 5,000円 |
| B社 | 5,000時間 | 7,000円 |
→ B社は40%高いが、B10は67%長い → 長期的にはB社がお得かも
🏭 活用シーン③:保証期間の設定
💡 メーカーの保証期間の考え方
製品の保証期間は、B1〜B5程度に設定されることが多いです。
理由:保証期間内の故障を1〜5%以下に抑えたいから。
例:B5 = 1,000時間 の製品 → 保証期間を「1,000時間または1年」に設定
📝 まとめ
✅ この記事のポイント
-
B10ライフとは、「全体の10%が故障するまでの時間」
=「90%がまだ生き残っている時間」 -
Bxライフ:xを変えればいろんな寿命が分かる
B1, B5, B10, B50 など用途に応じて使い分け -
B10が業界標準の理由
実験しやすい、安全マージンがある、歴史的に定着 -
計算公式:Bx = η × [ln(1/(1−x/100))]1/m
ワイブル分布のm、ηから計算可能 - 実務活用:保全計画、部品選定、保証期間の設定
🔑 覚えておくべき公式
B10ライフ
B10 = η × [0.1054]1/m
Bxライフ(一般形)
Bx = η × [ln(1/(1−x/100))]1/m
ポイント:B10 < η(特性寿命)は常に成り立つ
💡 B10とηの関係を覚えるコツ
η(イータ):約63%が故障する時間 → 「過半数がダメになる時間」
B10:10%が故障する時間 → 「そろそろ壊れ始める時間」
B10で交換すれば、90%は無事という安全マージンの考え方!
🚀 次に読むべき記事
B10ライフを理解できたら、次は「ワイブル確率紙」を学びましょう。
実際の故障データからm、ηを推定する方法がわかります。
📖 NEXT STEP
【実務向け】信頼性データの取り方|打ち切りデータ(中途・定時・定数)の扱い方
寿命試験で得られる「打ち切りデータ」の種類と扱い方を図解。実務での信頼性データ収集の基礎をマスターします。
📚 関連記事
【図解】ワイブル分布とは?|形状パラメータmで故障パターンを見抜く 信頼性指標
【図解】MTBFとMTTFの違い|"修理できるか"で使い分ける2つの指標 故障率曲線
【完全図解】故障率曲線(バスタブカーブ)|製品の"寿命"を3つの期間で理解する 可用性
【図解】アベイラビリティ(可用性)とは?|"使いたいときに使える確率"を計算する
📖 信頼性工学シリーズ
- 信頼性工学とは?
- MTBFとMTTFの違い
- 故障率曲線(バスタブカーブ)
- アベイラビリティ(可用性)
- 信頼性ブロック図
- ワイブル分布
- B10ライフ ← 今ここ
- 打ち切りデータ ← 次はこれ!
- ワイブル確率紙(準備中)
💡 B10ライフは、「安全マージンを持った寿命」を表す実務で超重要な指標です。
カタログでB10を見つけたら、「10%が壊れる時間」と読み替えましょう!
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。