😓「同じ条件で複数回測定したデータ、どう扱えばいいの?」
😓「残差が大きいのは、測定誤差?それとも直線が合ってない?」
😓「Lack of Fit検定って何を検定しているの?」
こんな疑問、抱えていませんか?
実験データでは、同じxの値で複数回測定することがよくあります。この「繰り返しデータ」を活用すると、通常の回帰分析では見えなかった情報が得られます。
💡 結論ファースト
繰り返しのある回帰分析では、残差を「純誤差(測定のバラつき)」と「当てはめの悪さ(モデルのズレ)」に分解できます。これにより「直線モデルで本当にいいのか?」を統計的に検定(Lack of Fit検定)できます。
📚 この記事でわかること
- 繰り返しのある回帰分析のメリット
- 純誤差(Pure Error)と当てはめの悪さ(Lack of Fit)の違い
- Lack of Fit検定で直線モデルの妥当性を判定する方法
- 計算例で分散分析表を完成させる手順
📌 前提知識:単回帰の分散分析表を理解している方向けです。まだの方は以下もどうぞ。
→ 単回帰の分散分析表|回帰・残差・全体の平方和
目次
🔄 繰り返しのある回帰分析とは?
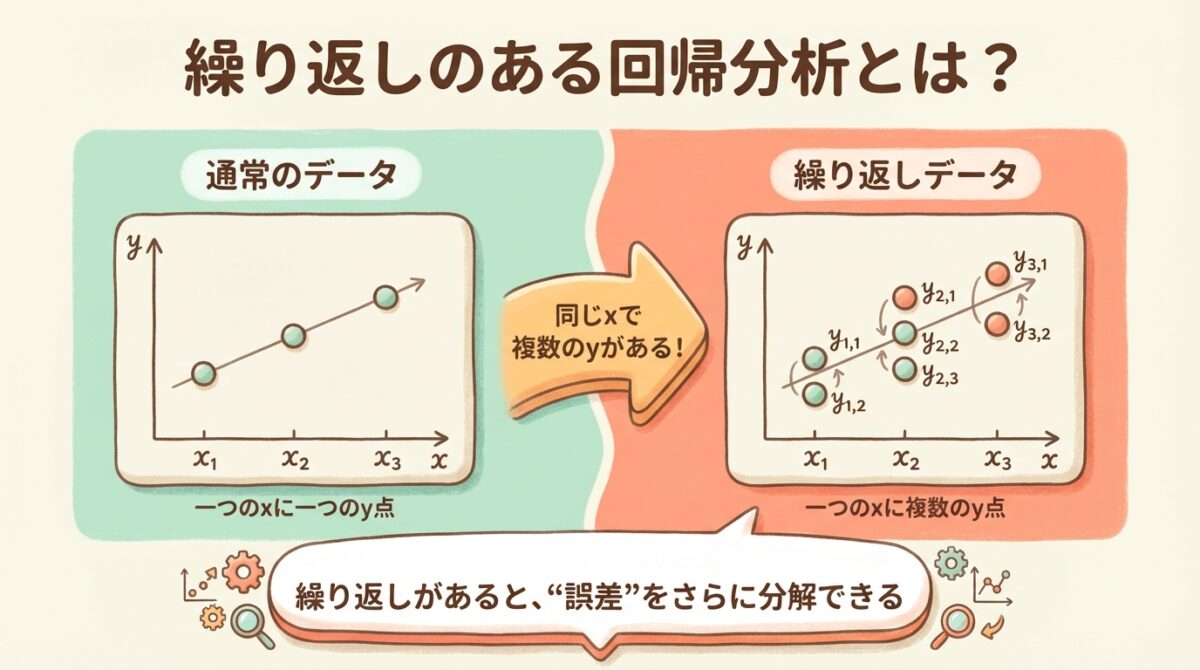
繰り返しのある回帰分析とは、同じxの値に対して複数のyが測定されているデータを扱う回帰分析です。
📊 通常の回帰 vs 繰り返しのある回帰
通常の回帰データ
| x | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| y | 2 | 4 | 5 | 4 | 6 |
各xに対してyは1つだけ
繰り返しのあるデータ
| x | 1 | 1 | 2 | 2 | 3 | 3 |
|---|---|---|---|---|---|---|
| y | 2 | 3 | 4 | 5 | 5 | 7 |
同じxに対して複数のyがある!
🤔 なぜ繰り返しデータが重要なのか?
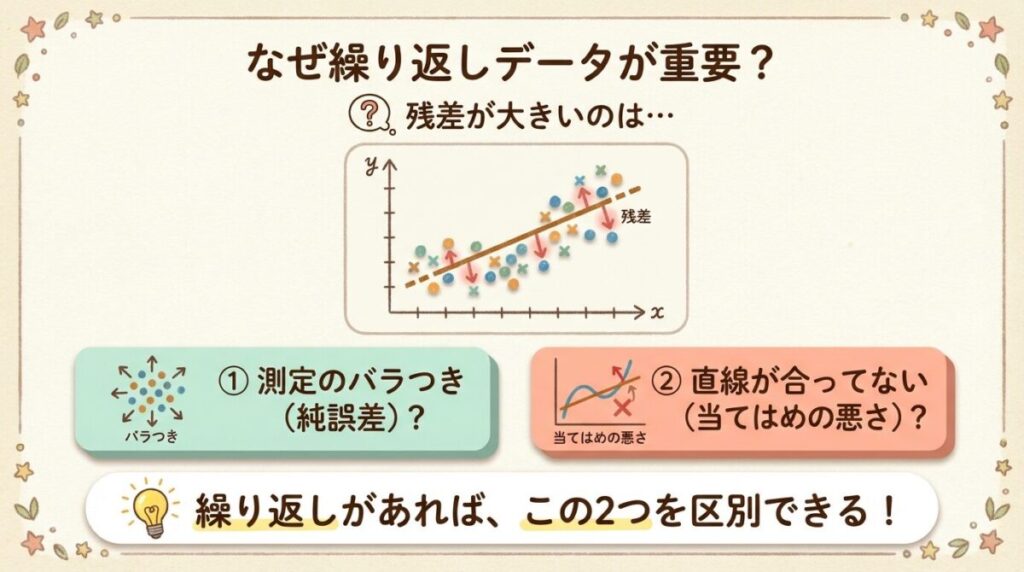
通常の回帰分析では、残差(y − ŷ)が大きいとき、その原因が2つ考えられます。
原因①:測定のバラつき
同じxでも測定するたびにyが違う。これは避けられない誤差(純誤差)。
原因②:モデルのズレ
本当は曲線なのに直線で近似している。これは当てはめの悪さ(Lack of Fit)。
☕ イメージで理解:的当てゲーム
あなたが的を狙って矢を投げたとします。的の中心からズレた原因は2つ考えられます。
① 腕のブレ(純誤差):何度投げてもピッタリ同じ場所には当たらない
② 狙いのズレ(当てはめの悪さ):そもそも狙っている場所が中心からズレている
繰り返しデータがあれば、「腕のブレ」と「狙いのズレ」を分離して評価できます!
✨ 繰り返しデータがあると…
残差を「純誤差」と「当てはめの悪さ」に分解できる
→ 「直線モデルで本当にいいのか?」を検定できる
📐 残差の分解:純誤差と当てはめの悪さ
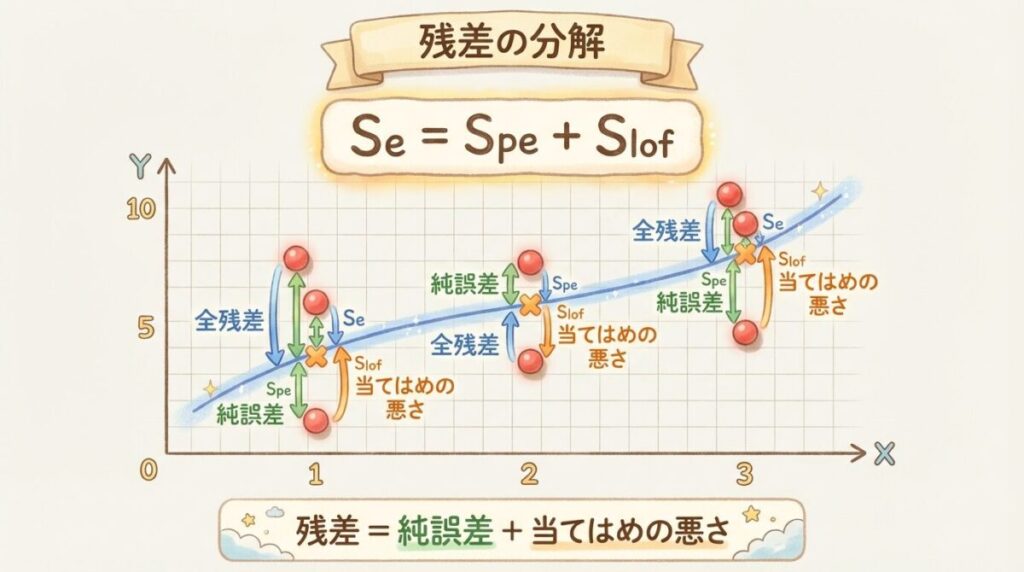
繰り返しのある回帰分析では、残差平方和Seを2つに分解します。
🎯 残差分解の基本式
Se = SPE + SLOF
残差平方和 = 純誤差 + 当てはめの悪さ
📊 各平方和の定義
記号の定義:
m = xの水準数(異なるxの種類)
ni = 水準iでの繰り返し数
N = 全データ数(= Σni)
ȳi = 水準iでのyの平均
ŷi = 水準iでの回帰による予測値
SLOF:当てはめの悪さ(Lack of Fit)
SLOF = Σi ni(ȳi − ŷi)²
意味:グループ平均と回帰直線のズレ(モデルの不適合)
自由度:m − 2
📈 図解イメージ
同じxの値に複数のyがあるとき…
SPE(純誤差)
各点 yij → グループ平均 ȳi
「同じxなのにバラつく」
SLOF(当てはめの悪さ)
グループ平均 ȳi → 予測値 ŷi
「平均が直線から外れる」
⚖️ Lack of Fit検定(当てはめの妥当性検定)
「直線モデルで本当にいいのか?」を統計的に検定します。
Lack of Fit検定
帰無仮説 H₀:直線モデルは適切(当てはめの悪さは純誤差と同程度)
対立仮説 H₁:直線モデルは不適切(当てはめの悪さが大きい)
FLOF = VLOF/VPE = SLOF/(m−2)/SPE/(N−m)
FLOF > F(m−2, N−m; α) ならば 直線モデルは不適切
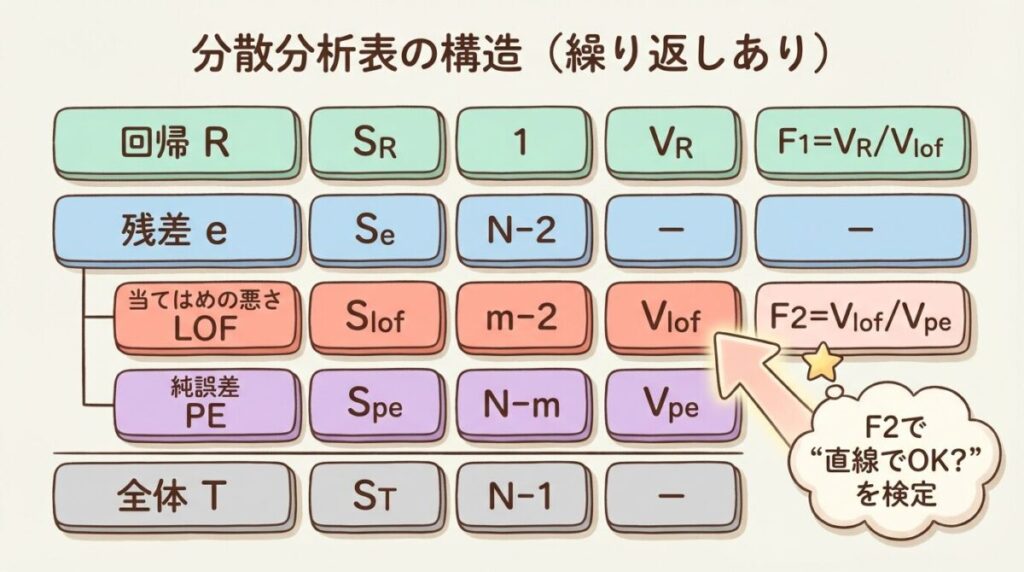
📋 分散分析表の構造(繰り返しあり)
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F値 |
|---|---|---|---|---|
| 回帰 R | SR | 1 | VR | FR = VR/VPE |
| 残差 e | Se | N − 2 | − | − |
| └ 当てはめの悪さ LOF | SLOF | m − 2 | VLOF | FLOF = VLOF/VPE |
| └ 純誤差 PE | SPE | N − m | VPE | − |
| 全体 T | ST | N − 1 | − | − |
🧮 計算例:繰り返しのあるデータ
データ(N = 6, m = 3水準, 各水準で繰り返し2回)
| i | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| x | 1 | 1 | 2 | 2 | 3 | 3 |
| y | 2 | 3 | 4 | 5 | 5 | 7 |
Step 1:グループ平均の計算
| 水準 xi | y の値 | グループ平均 ȳi |
|---|---|---|
| 1 | 2, 3 | 2.5 |
| 2 | 4, 5 | 4.5 |
| 3 | 5, 7 | 6.0 |
全体平均:ȳ = (2+3+4+5+5+7)/6 = 26/6 ≈ 4.33
Step 2:回帰係数の計算
x̄ = (1+1+2+2+3+3)/6 = 2
Σ(x−x̄)(y−ȳ) = (−1)(−2.33) + (−1)(−1.33) + (0)(−0.33) + (0)(0.67) + (1)(0.67) + (1)(2.67) = 2.33 + 1.33 + 0 + 0 + 0.67 + 2.67 = 7
Σ(x−x̄)² = 1 + 1 + 0 + 0 + 1 + 1 = 4
傾き b = 7/4 = 1.75
切片 a = 4.33 − 1.75 × 2 = 0.83 → 回帰式:ŷ = 0.83 + 1.75x
Step 3:予測値の計算
| 水準 x | ŷ = 0.83 + 1.75x | ȳi | ȳi − ŷ |
|---|---|---|---|
| 1 | 2.58 | 2.5 | −0.08 |
| 2 | 4.33 | 4.5 | +0.17 |
| 3 | 6.08 | 6.0 | −0.08 |
Step 4:各平方和の計算
ST(全体)= Σ(y−ȳ)² = (−2.33)² + (−1.33)² + (−0.33)² + (0.67)² + (0.67)² + (2.67)² = 5.43 + 1.77 + 0.11 + 0.45 + 0.45 + 7.13 = 15.33
SR(回帰)= b × Σ(x−x̄)(y−ȳ) = 1.75 × 7 = 12.25
Se(残差)= ST − SR = 15.33 − 12.25 = 3.08
SPE(純誤差)= Σグループ内変動
= [(2−2.5)² + (3−2.5)²] + [(4−4.5)² + (5−4.5)²] + [(5−6)² + (7−6)²]
= [0.25 + 0.25] + [0.25 + 0.25] + [1 + 1] = 0.5 + 0.5 + 2 = 3.0
SLOF(当てはめの悪さ)= Se − SPE = 3.08 − 3.0 = 0.08
📊 完成した分散分析表
| 要因 | S | φ | V | F |
|---|---|---|---|---|
| 回帰 R | 12.25 | 1 | 12.25 | FR = 12.25 |
| 残差 e | 3.08 | 4 | − | − |
| └ LOF | 0.08 | 1 | 0.08 | 0.08 |
| └ PE | 3.00 | 3 | 1.00 | − |
| 全体 T | 15.33 | 5 | − | − |
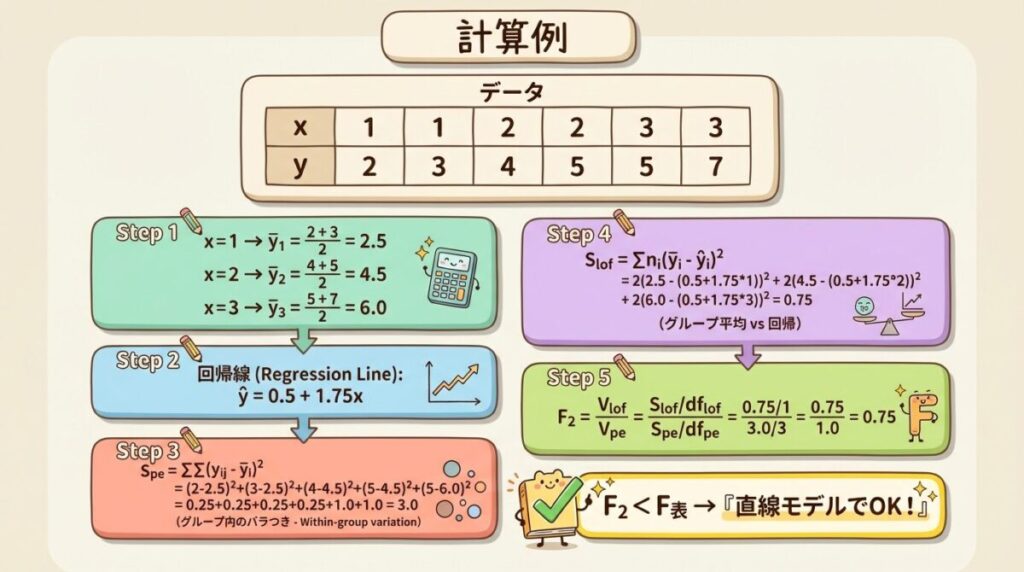
⚖️ 検定の判定
🔍 Step 1:Lack of Fit検定(直線モデルの妥当性)
FLOF = VLOF / VPE = 0.08 / 1.00 = 0.08
F分布表より:F(1, 3; 0.05) = 10.13
判定:FLOF = 0.08 < 10.13 → 直線モデルは適切(H₀を棄却できない)
✅ 直線モデルは妥当!
当てはめの悪さは純誤差と同程度なので、直線で近似してOK
🔍 Step 2:回帰の有意性検定
FR = VR / VPE = 12.25 / 1.00 = 12.25
F分布表より:F(1, 3; 0.05) = 10.13
判定:FR = 12.25 > 10.13 → 回帰は有意(H₀を棄却)
🎯 最終結論
① 直線モデルは適切(Lack of Fit検定で有意でない)
② xはyに有意な影響を与える(回帰の有意性検定で有意)
→ 回帰式 ŷ = 0.83 + 1.75x は妥当で、予測に使える
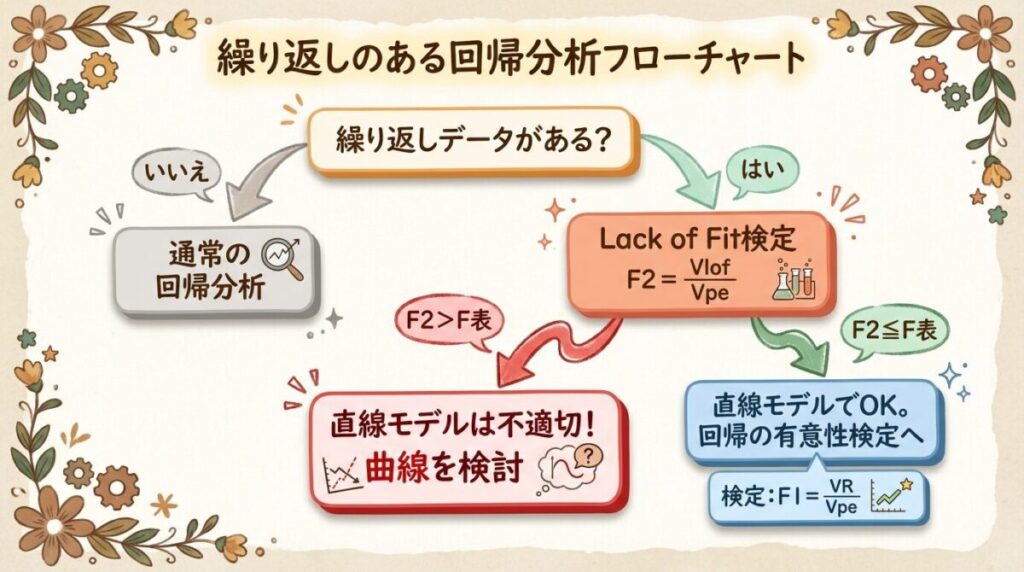
📋 検定の手順フローチャート
↓
FLOF = VLOF / VPE
FLOF > F表
↓
曲線モデルを検討
FLOF ≤ F表
↓
Step 2へ
↓
FR = VR / VPE
📌 まとめ
- 繰り返しデータがあると、残差を「純誤差」と「当てはめの悪さ」に分解できる
- SPE:グループ内のバラつき(測定誤差)
- SLOF:グループ平均と回帰直線のズレ(モデルの不適合)
- Lack of Fit検定で「直線モデルでいいか?」を判定
- LOF検定が有意でなければ、回帰の有意性検定へ進む
💡 試験対策のポイント
QC検定では「繰り返しのある回帰分析」の分散分析表を埋める問題が出題されます。自由度の分解(N−2 = (m−2) + (N−m))と2段階の検定(①LOF検定→②回帰の検定)を確実に押さえましょう。
最後までお読みいただきありがとうございました!
ご質問・ご感想は @shirasusolo までお気軽にどうぞ。
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。