- 擬水準法の分散分析で「二元表を作る」と言われても、なぜ必要なのかわからない
- 形式的因子Pと実際の因子Aの平方和が違う理由がピンとこない
- 自由度の計算で混乱してしまう
- なぜ擬水準法では「二元表」が必要なのか、その本質的な理由
- 擬水準あり/なしで平方和の計算方法がどう変わるか
- 例題を通じた具体的な計算手順
【前編】では、擬水準法の考え方と割り付け方法を解説しました。
この後編では、「なぜ擬水準法では二元表が必要なのか?」という本質的な疑問に答えながら、分散分析の計算方法を解説します。
【完全図解】擬水準法とは?|2水準系直交表に3水準因子を入れる「裏技」をL8で徹底解説 →
目次
核心|なぜ「二元表」が必要なのか?
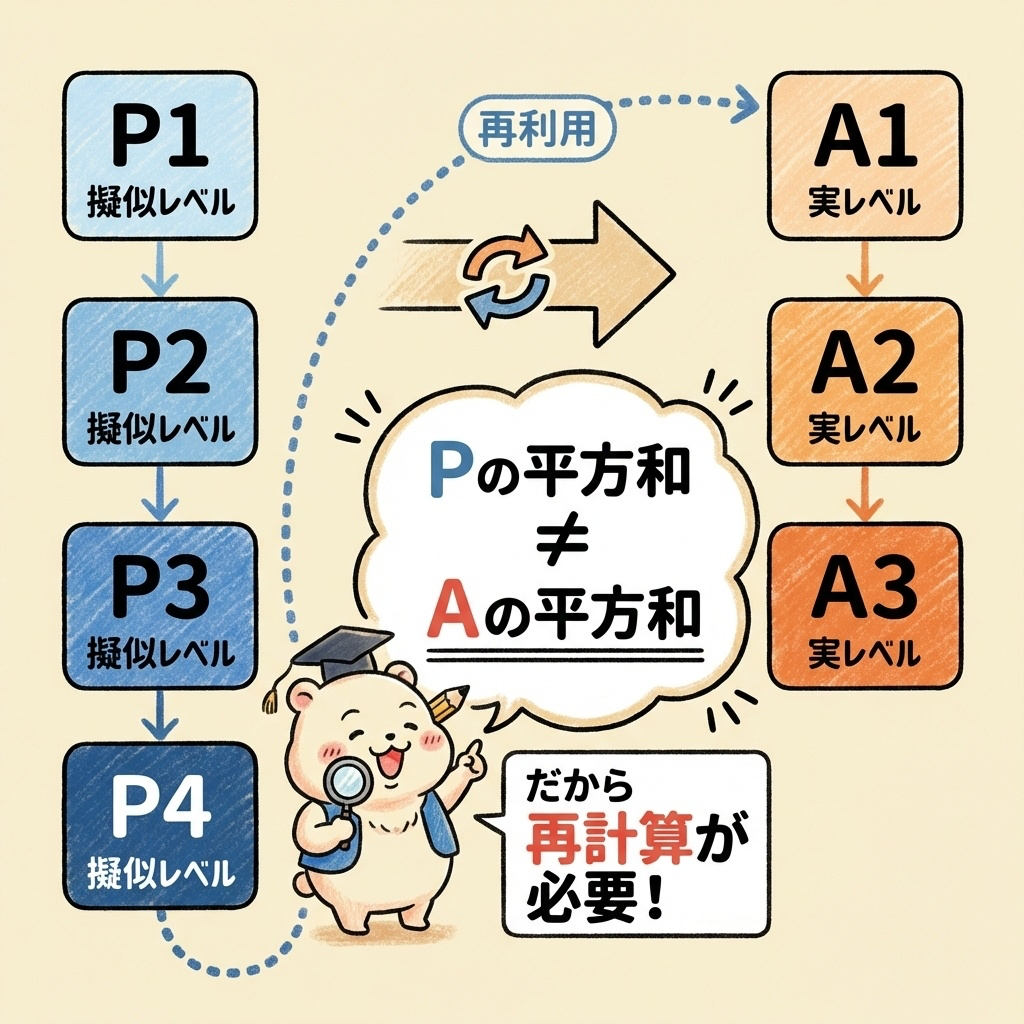
擬水準法の分散分析を理解するカギは、「形式的因子P」と「実際の因子A」は別物という点です。
形式的因子Pと実際の因子Aの関係
前編で学んだように、擬水準法では3水準因子Aを「形式的な4水準因子P」として割り付けます。
| 形式的4水準P | 実際の3水準A | 実験回数 |
|---|---|---|
| P₁ | A₁ | 2回 |
| P₂ | A₂ | 2回 |
| P₃ | A₃ | 2回 |
| P₄(擬水準) | A₁(再利用) | 2回 |
ここで重要なのは、P₁とP₄は「別の水準」として扱われるが、実際はどちらもA₁ということです。
列の平方和はPの平方和であり、Aの平方和ではない
直交表の[1][2][3]列から計算した平方和は、「P₁、P₂、P₃、P₄の4水準の違い」による変動を測っています。
しかし、私たちが知りたいのは「A₁、A₂、A₃の3水準の違い」による変動ですよね。
SP(列の平方和の合計)≠ SA(実際の因子Aの平方和)
だから、因子Aの平方和は二元表を作って計算し直す必要があるのです。
イメージで言うと、「P₁とP₄の違い」は列の平方和に含まれていますが、実際は両方ともA₁なので、因子Aの効果としては「同じもの」として合算しなければなりません。
例題|クッキーのサクサク感を改善する実験
では、具体的な例題で計算していきましょう。
因子A(小麦粉):3水準(A₁:薄力粉を擬水準に選択、A₂:中力粉、A₃:強力粉)
因子B(温度):2水準(B₁:160℃、B₂:180℃)
使用直交表:L8(擬水準法で因子Aを[1][2][3]列に割り付け)
実験データと各列の平方和
実験を行い、各列の平方和を計算したところ、以下の結果が得られました。
| 列 | 割り付け | 列平方和 S[k] |
|---|---|---|
| [1] | P(因子A) | 18.0 |
| [2] | P(因子A) | 0.5 |
| [3] | P(因子A) | 4.5 |
| [4] | 因子B | 4.5 |
| [5] | P×B | 4.5 |
| [6] | P×B | 0.0 |
| [7] | P×B | 2.0 |
| 合計(= 総平方和 ST) | 34.0 | |
また、修正項 CT = 338.0 とします。

計算①|擬水準を含まない因子の平方和
まず、擬水準を含まない因子から計算します。こちらは簡単です。
因子Bの平方和:列の平方和をそのまま使う
因子Bは[4]列に割り付けられており、擬水準を含みません。
SB = S[4] = 4.5
形式的因子Pの平方和:3列の合計
形式的因子Pの平方和は、[1][2][3]列の平方和を合計したものです。
SP = S[1] + S[2] + S[3] = 18.0 + 0.5 + 4.5 = 23.0
P×Bの平方和:3列の合計
SP×B = S[5] + S[6] + S[7] = 4.5 + 0.0 + 2.0 = 6.5
- SB = 4.5(これは最終的な分散分析表にそのまま使える)
- SP = 23.0(形式的因子P。実際の因子Aの平方和ではない)
- SP×B = 6.5(形式的なP×B。実際のA×Bの平方和ではない)

計算②|AB二元表を作成する
次に、擬水準を含む因子Aの平方和を求めるために、AB二元表を作成します。
実験データを、因子Aと因子Bの組み合わせごとに整理した表です。
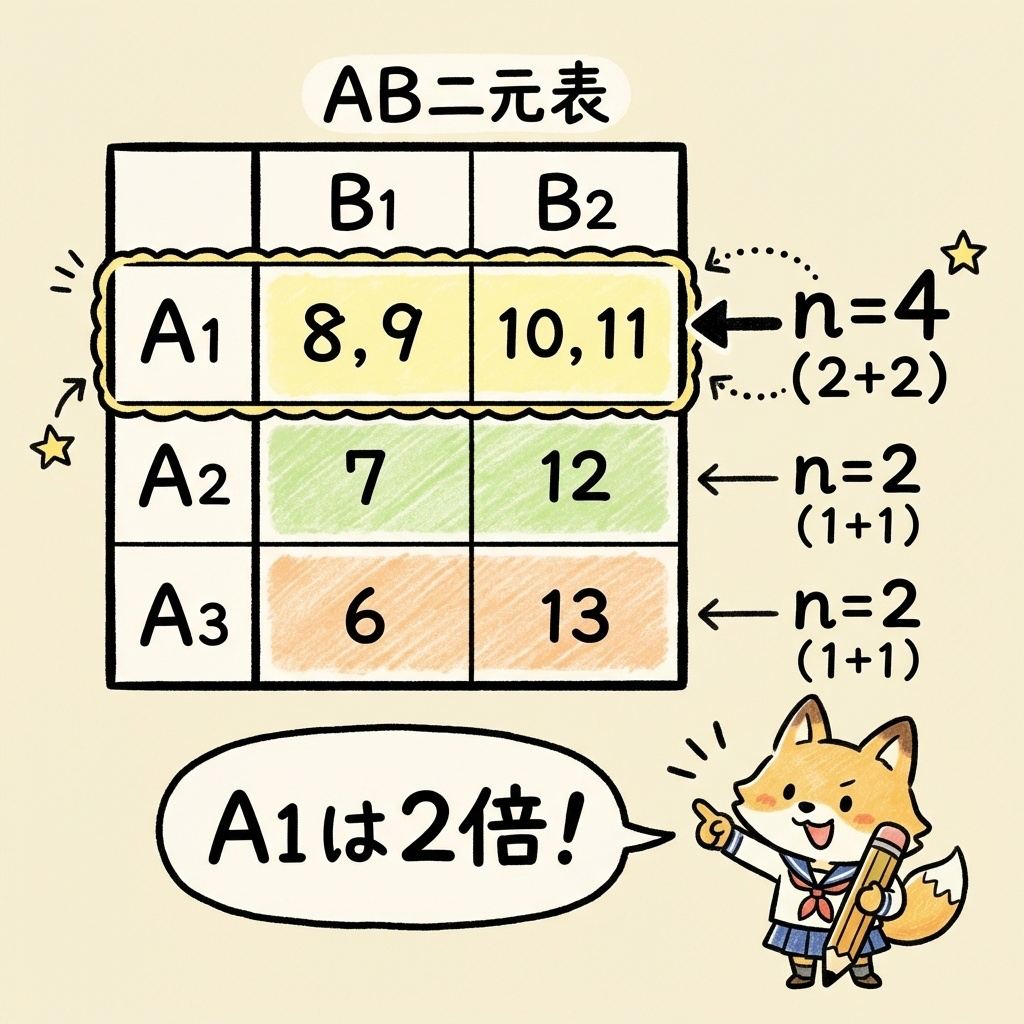
AB二元表(セル合計)
| B₁ | B₂ | A水準の合計 | データ数 n | |
|---|---|---|---|---|
| A₁ | 15(n=2) | 14(n=2) | 29 | 4 |
| A₂ | 6(n=1) | 2(n=1) | 8 | 2 |
| A₃ | 8(n=1) | 7(n=1) | 15 | 2 |
| B水準の合計 | 29 | 23 | 52 | 8 |
- A₁(擬水準):データ数 n = 4(各セル2個ずつ)
- A₂、A₃:データ数 n = 2(各セル1個ずつ)
この繰返し数の違いが、平方和の計算に影響します。
【初心者向け】繰返しのある二元配置実験とは? →
計算③|因子Aの平方和SAを求める
AB二元表から、実際の因子Aの平方和を計算します。
繰返し数が不均等なときの公式
各水準の繰返し数(データ数)が異なるので、それぞれの繰返し数で割ります。
計算の実行
= 210.25 + 32 + 112.5 − 338.0
= 354.75 − 338.0
= 16.75
- 形式的因子Pの平方和:SP = 23.0
- 実際の因子Aの平方和:SA = 16.75
SP − SA = 23.0 − 16.75 = 6.25
この差は「P₁とP₄の違い」によるもので、実際はどちらもA₁なので、因子Aの効果には含まれません。
計算④|交互作用A×Bの平方和を求める
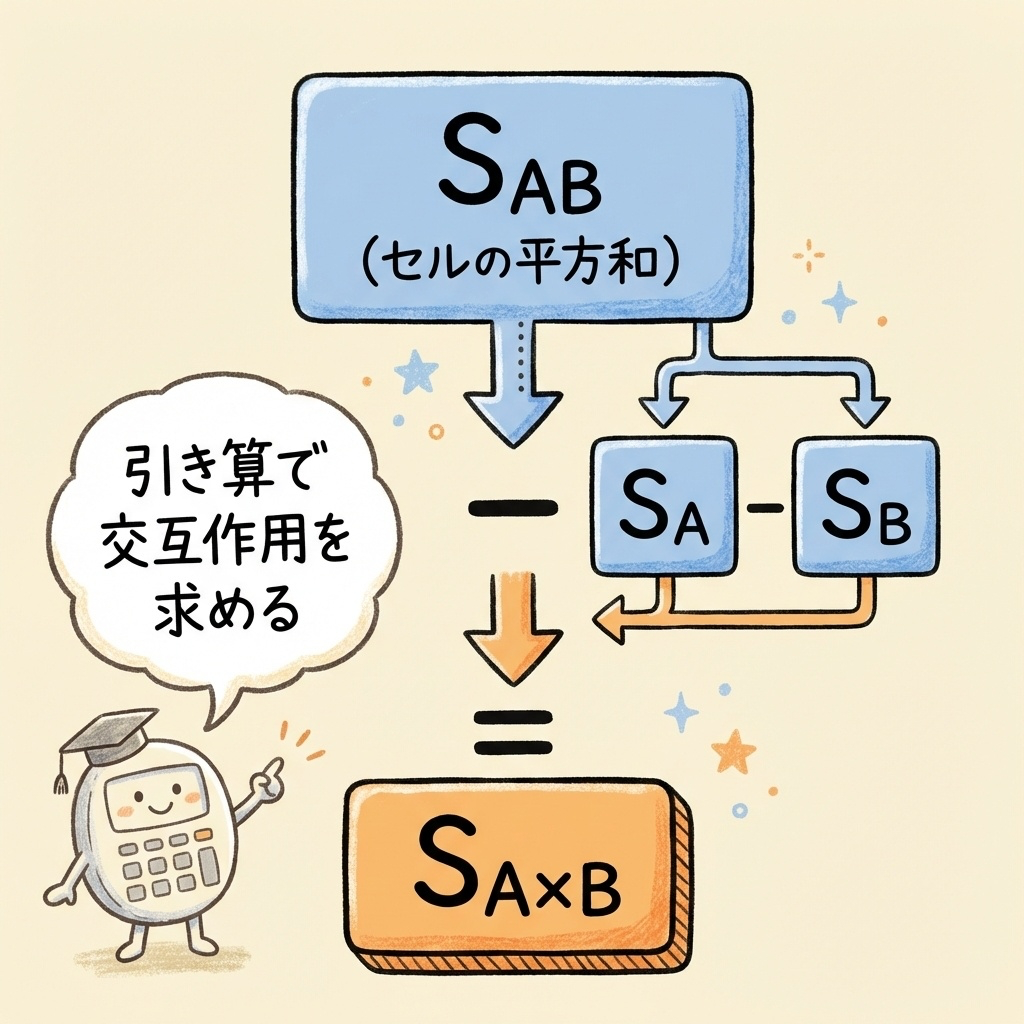
交互作用の平方和は、「セルの平方和」から「主効果の平方和」を引くことで求めます。
Step1:セルの平方和SABを計算
各セルの合計を、そのセルの繰返し数で割って足し合わせます。
= 112.5 + 98 + 36 + 4 + 64 + 49 − 338.0
= 363.5 − 338.0
= 25.5
Step2:交互作用A×Bの平方和を計算
SA×B = SAB − SA − SB
SA×B = 25.5 − 16.75 − 4.5 = 4.25
- 形式的なP×Bの平方和:SP×B = 6.5
- 実際のA×Bの平方和:SA×B = 4.25
計算⑤|誤差の平方和SEを求める
誤差の平方和は、2つの方法で求められます。どちらでも同じ結果になります。
方法①:総平方和から各要因を引く
SE = ST − SA − SB − SA×B
= 34.0 − 16.75 − 4.5 − 4.25 = 8.5
方法②:形式的因子との差から求める
SE = (SP − SA)+(SP×B − SA×B)
= (23.0 − 16.75)+(6.5 − 4.25)
= 6.25 + 2.25 = 8.5
方法②の「SP − SA」は、P₁とP₄(実際は同じA₁)の「見かけ上の違い」による変動です。
これは因子Aの効果ではなく「誤差」として扱われるべきものなので、誤差の平方和に含まれます。
計算⑥|自由度を計算する
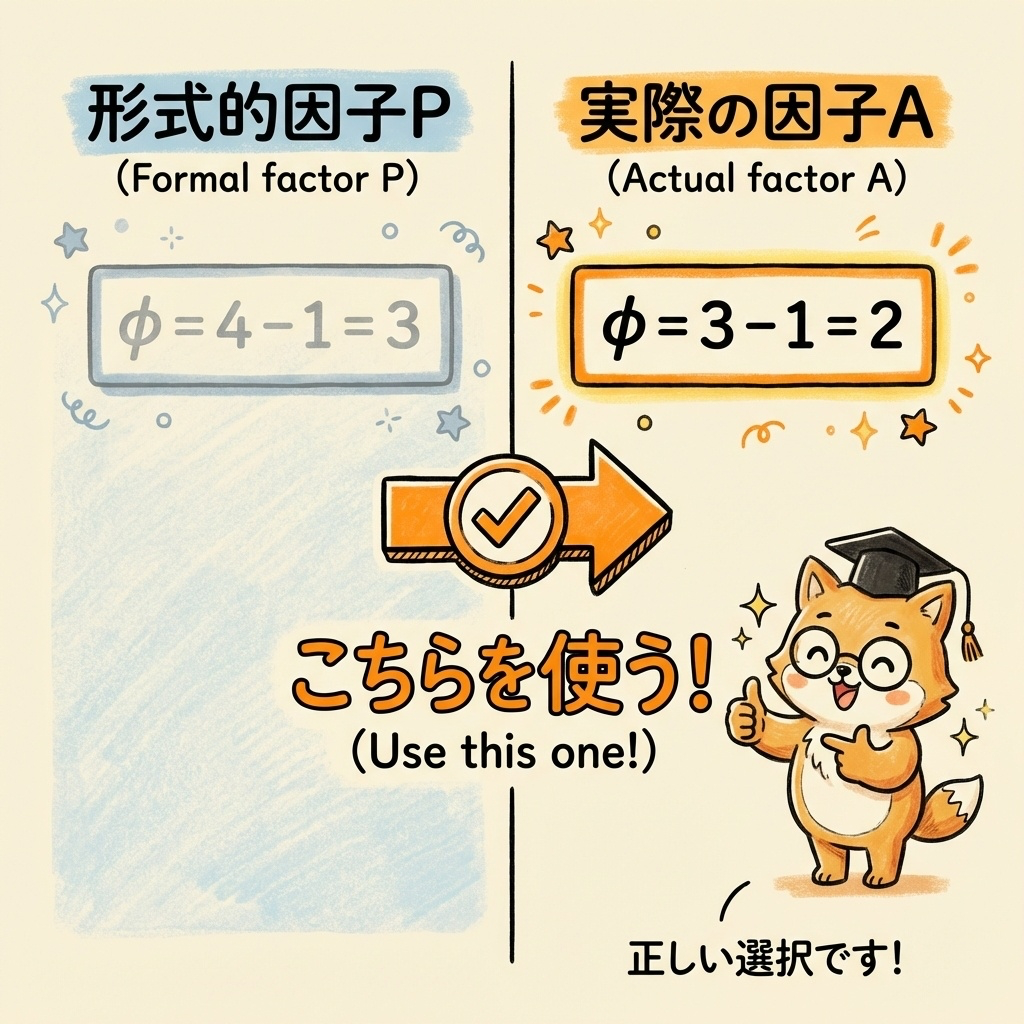
最後に、自由度を計算します。形式的因子Pではなく、実際の因子Aの自由度を使うことに注意してください。
| 要因 | 公式 | 計算 | 自由度 φ |
|---|---|---|---|
| (参考)形式的因子P | 4 − 1 | - | 3 |
| 因子A(実際) | 水準数 − 1 | 3 − 1 | 2 |
| 因子B | 水準数 − 1 | 2 − 1 | 1 |
| A×B(実際) | φA × φB | 2 × 1 | 2 |
| 誤差E | φT − φA − φB − φA×B | 7 − 2 − 1 − 2 | 2 |
| 合計T | データ数 − 1 | 8 − 1 | 7 |
形式的因子Pの自由度(φ = 3)を使ってしまうミスが多いです。
分散分析表に載せるのは実際の因子Aの自由度(φ = 2)です。
完成|分散分析表
すべての計算結果をまとめて、分散分析表を完成させます。
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F₀ |
|---|---|---|---|---|
| A | 16.75 | 2 | 8.375 | 1.97 |
| B | 4.50 | 1 | 4.50 | 1.06 |
| A×B | 4.25 | 2 | 2.125 | 0.50 |
| 誤差E | 8.50 | 2 | 4.25 | - |
| 合計T | 34.00 | 7 | - | - |
※ V = S ÷ φ、F₀ = V ÷ VE で計算
SA + SB + SA×B + SE = 16.75 + 4.50 + 4.25 + 8.50 = 34.00 = ST ✓
F検定で有意差を判定する|F分布表の使い方 →
まとめ|擬水準法の分散分析で押さえるべき3つのポイント
列の平方和の合計(SP)は、形式的4水準因子Pの平方和。
実際の3水準因子Aの平方和(SA)は、AB二元表から計算し直す必要がある。
擬水準に選んだ水準(例:A₁)は繰返し数が2倍になる。
平方和を計算するとき、各水準の繰返し数で割ることを忘れずに。
分散分析表に載せるのは実際の因子Aの自由度(φ = 水準数 − 1)。
形式的因子Pの自由度を使わないように注意。
📚 次に読むべき記事
擬水準法の概念と割り付け方法を復習したい方はこちら。
擬水準法の「兄弟分」である多水準作成法との違いを理解する。
実験計画法の全体像と学習順序を確認したい方はこちら。