📌 この記事の位置づけ
「実験計画法の基礎概念シリーズ」第8回。前回は「主効果」を学びました。今回は主効果だけでは見えない「交互作用」を解説します。
「主効果で最適条件を決めたのに、うまくいかない…」
「因子の組み合わせで結果が変わるってどういうこと?」
それは「交互作用」のせいかもしれません。
交互作用を理解すると、「なぜか最適条件が効かない」という失敗を防げるようになります。
目次
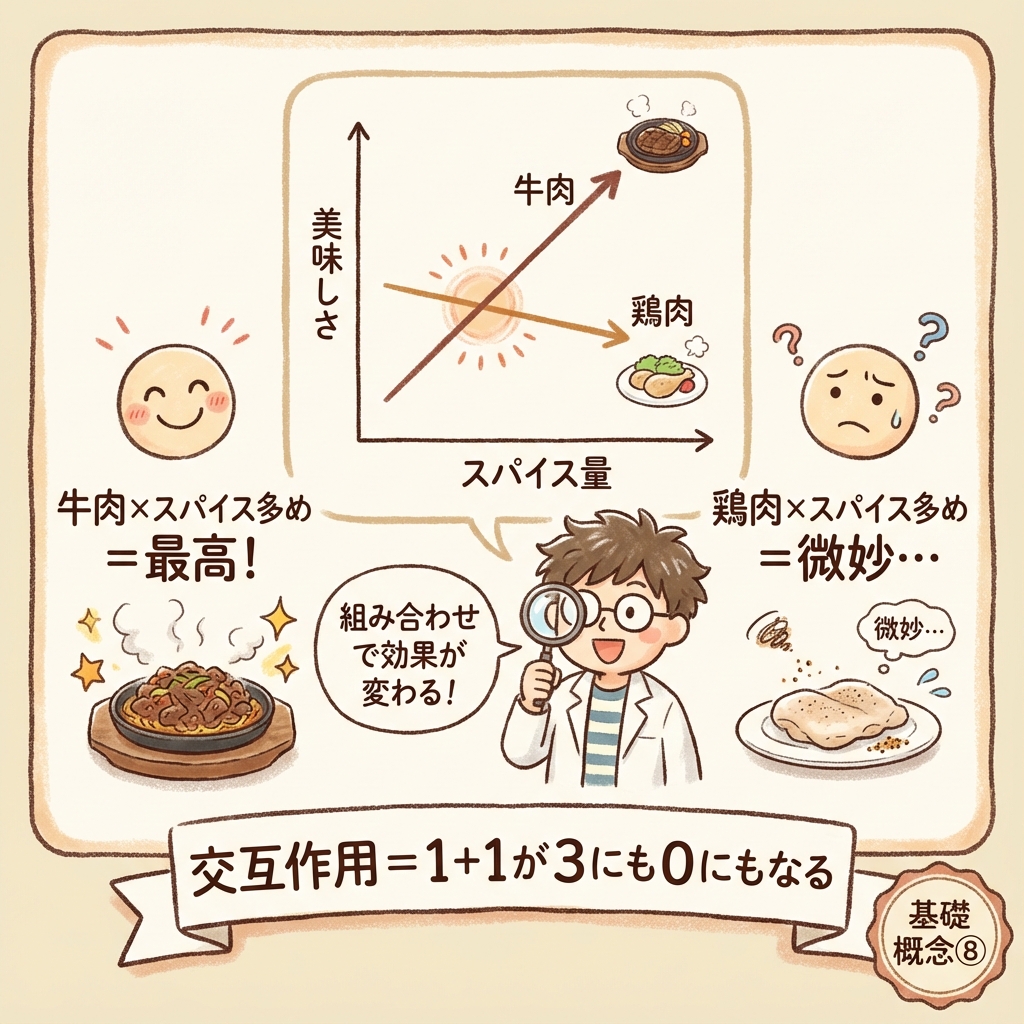
交互作用とは?【1+1が3にも0にもなる】
交互作用(こうごさよう)とは、因子の組み合わせによって生まれる特別な効果のことです。
英語では「Interaction(インタラクション)」と言います。
📖 交互作用の定義
ある因子の効果が、別の因子の水準によって変わる現象。
「A単独の効果」+「B単独の効果」では説明できない、組み合わせならではの効果。
言葉だけではピンとこないですよね。具体例で見てみましょう。
カレー作りで理解する交互作用
前回と同じく、カレーの実験を考えます。
| 因子 | 水準1 | 水準2 |
|---|---|---|
| A:肉の種類 | 鶏肉 🐔 | 牛肉 🐄 |
| B:スパイスの量 | 少なめ | 多め |
📊 交互作用がない場合(前回の例)
前回の実験結果を思い出してください。
| スパイス少なめ | スパイス多め | 差 | |
|---|---|---|---|
| 鶏肉 🐔 | 60点 | 64点 | +4点 |
| 牛肉 🐄 | 80点 | 84点 | +4点 |
スパイスを増やすと、鶏肉でも牛肉でも+4点です。
これは交互作用がない状態。因子Bの効果が、因子Aに関係なく一定です。
📊 交互作用がある場合
では、こんな結果だったらどうでしょう?
| スパイス少なめ | スパイス多め | 差 | |
|---|---|---|---|
| 鶏肉 🐔 | 60点 | 62点 | +2点 |
| 牛肉 🐄 | 70点 | 90点 | +20点 |
今度は全然違いますね。
🔥 これが交互作用!
- 鶏肉のとき:スパイス増やしても+2点しか変わらない
- 牛肉のとき:スパイス増やすと+20点も上がる!
→ スパイスの効果が、肉の種類によって全然違う!
これが交互作用です。因子Bの効果が、因子Aの水準によって変わるのです。
交互作用を図で理解する
交互作用の有無は、グラフにするとわかりやすいです。
📈 交互作用がない場合:線が平行
交互作用なし(線が平行)
スコア
90 ┤
80 ┤ ●━━━● 牛肉
70 ┤
60 ┤ ○━━━○ 鶏肉
50 ┤
└───┬───┬───→ スパイス
少 多
→ どちらの肉でも、スパイスの効果は同じ
📈 交互作用がある場合:線が交差 or 傾きが違う
交互作用あり(線が交差)
スコア
90 ┤ ● 牛肉
80 ┤
70 ┤ ●╱
60 ┤ ○━━━○ 鶏肉
50 ┤
└───┬───┬───→ スパイス
少 多
→ 牛肉のときだけ、スパイスの効果が大きい
💡 覚え方
線が平行 → 交互作用なし
線が交差 or 傾きが違う → 交互作用あり
日常生活での交互作用の例
交互作用は、実は身近なところにもあります。
| 因子A | 因子B | 交互作用 |
|---|---|---|
| 薬💊 | お酒🍺 | 薬単独なら安全、でもお酒と一緒だと危険 |
| コーヒー☕ | ミルク🥛 | 苦いコーヒーも、ミルクを入れるとまろやか |
| 筋トレ💪 | 睡眠😴 | 筋トレしても、睡眠不足だと効果半減 |
「単独では良い効果」でも、「組み合わせると効果が変わる」ことがあるのです。
なぜ交互作用を知る必要があるのか?
交互作用を無視すると、最適条件を間違えることがあります。
❌ 主効果だけで判断した場合の失敗
主効果を計算すると…
・因子A(肉):牛肉の方が良い
・因子B(スパイス):多めの方が良い
→ 「牛肉×スパイス多め」が最適!
でも、もし「牛肉×スパイス多め」だと苦くなりすぎて不評だったら…?
交互作用を見落としていた可能性あり!
詳しくは次の記事「交互作用を無視すると失敗する?」で解説します。
まとめ
📌 この記事のポイント
- 交互作用=因子の組み合わせで生まれる特別な効果
- ある因子の効果が、別の因子の水準によって変わる現象
- グラフで線が平行→交互作用なし、線が交差→交互作用あり
- 交互作用を無視すると、最適条件を間違えるリスクがある
次の記事では、「交互作用を無視すると失敗する理由」を具体例で解説します。主効果だけで判断することの危険性を理解しましょう。
📚 次に読む記事
主効果だけ見て最適条件を決めると失敗する?交互作用を無視した解析の危険性と、「最適条件なのに上手くいかない」を防ぐ考え方を解説します。
交互作用を無視すると失敗する?|基礎概念⑨ →関連記事【あなたの悩みを解決】
🤔「主効果の計算方法を復習したい」
→ 主効果とは?因子の影響度を数値化する方法|基礎概念⑦🤔「二元配置実験で交互作用を解析したい」
→ 【完全図解】二元配置実験の計算方法|交互作用まで手を動かして理解する🤔「繰り返しありの二元配置で交互作用を検出したい」
→ 繰返しのある二元配置実験とは?交互作用も確実に検出する方法🤔「直交表で交互作用を調べる方法を知りたい」
→ 線点図の正体|なぜ点と線?「L4」で学ぶ割り付け入門🤔「交互作用を無視した解析のやり方を知りたい」
→ 交互作用を無視した解析とは?主効果だけを見るときのリスク🤔「実験計画法の全体像を把握したい」
→ 【完全版】実験計画法の学習マップ|基礎から応用まで体系的に学ぶ🤔「QC検定対策として学びたい」
→ 【合格体験記】知識ゼロから半年でQC検定2級に合格した勉強法🤔「因子と水準の基本を復習したい」
→ 因子と水準の違いとは?基本用語を図解で解説|基礎概念③