-

-
【完全図解】主成分得点とは?|「新しい成績表」で各サンプルの立ち位置をスッキリ理解
2026/1/25 主成分分析
😵 こんな疑問ありませんか? 「主成分得点」って結局何の数字なの? 固有値や寄与率はわかったけど、最終的に何を計算すればいいの? 散布図の点は何を表しているの? ✅ この ...
-
-
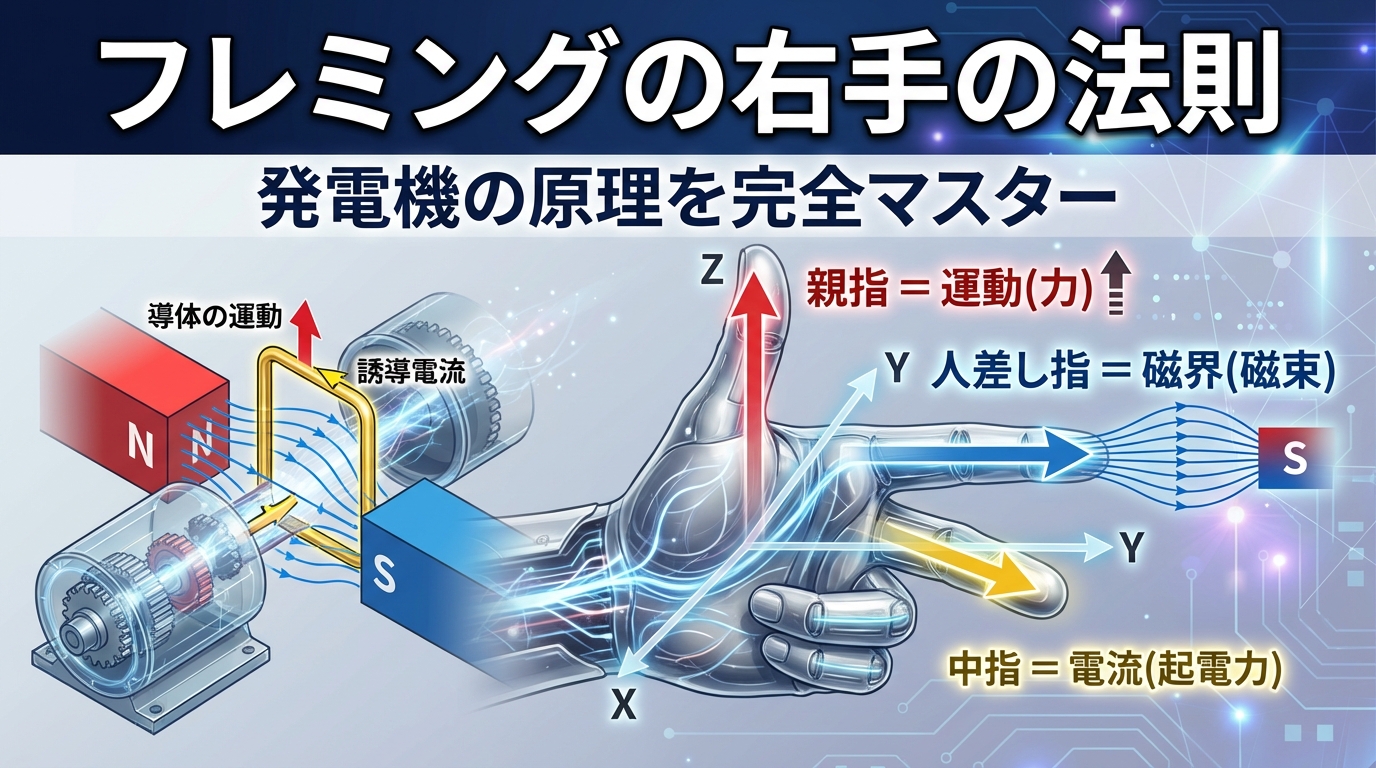
【電験三種・理論】フレミングの右手の法則|発電機の原理
2025/12/24 電磁誘導
⚡ こんな疑問、ありませんか? 「発電機ってどうやって電気を作ってるの?」「フレミングの右手の法則って何?」「なんで右手なの?左手じゃダメなの?」 結論から言うと、フレミングの右手の法則 ...
-
-
【電験三種・理論】レンツの法則|誘導電流の向きを決める右ねじの法則
2025/12/24
「レンツの法則って何?」「誘導電流の向きはどうやって決まるの?」「右ねじの法則って、どう使うの?」 そんな疑問を抱えているあなたへ。電験三種で頻出のレンツの法則と右ねじの法則を、今日こそ完璧にマスター ...
-

-
HSS型HSPが飲み会後に反省会するのは何故か
2025/12/24 HSS型HSP
深夜2時47分。 布団の中で、スマホの明かりだけが顔を照らす。 「なんであんなこと言ったんだろう…」 飲み会での自分の発言が、頭の中で無限リピート再生される。声のトーン、表情、相手の反応。すべてが鮮明 ...
-
-
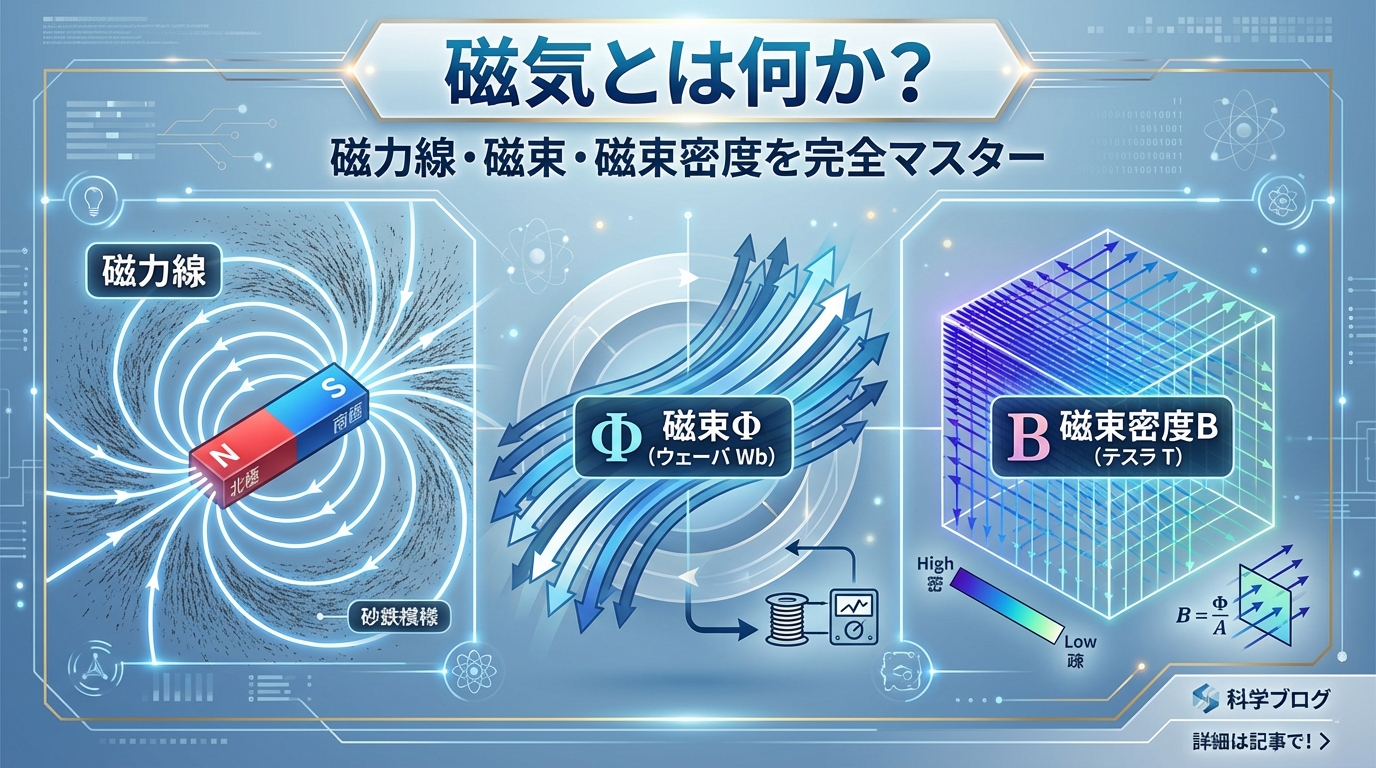
【電験三種・理論】磁気とは何か?|磁力線・磁束・磁束密度の基礎
2025/12/24 電磁気
「磁力線って何?」「磁束と磁束密度の違いがよく分からない…」「結局、磁気って何なの?」 そんな疑問を抱えているあなたへ。電験三種の理論分野で頻出の磁気の基礎を、今日こそ完璧にマスターしましょう。 結論 ...
-
-
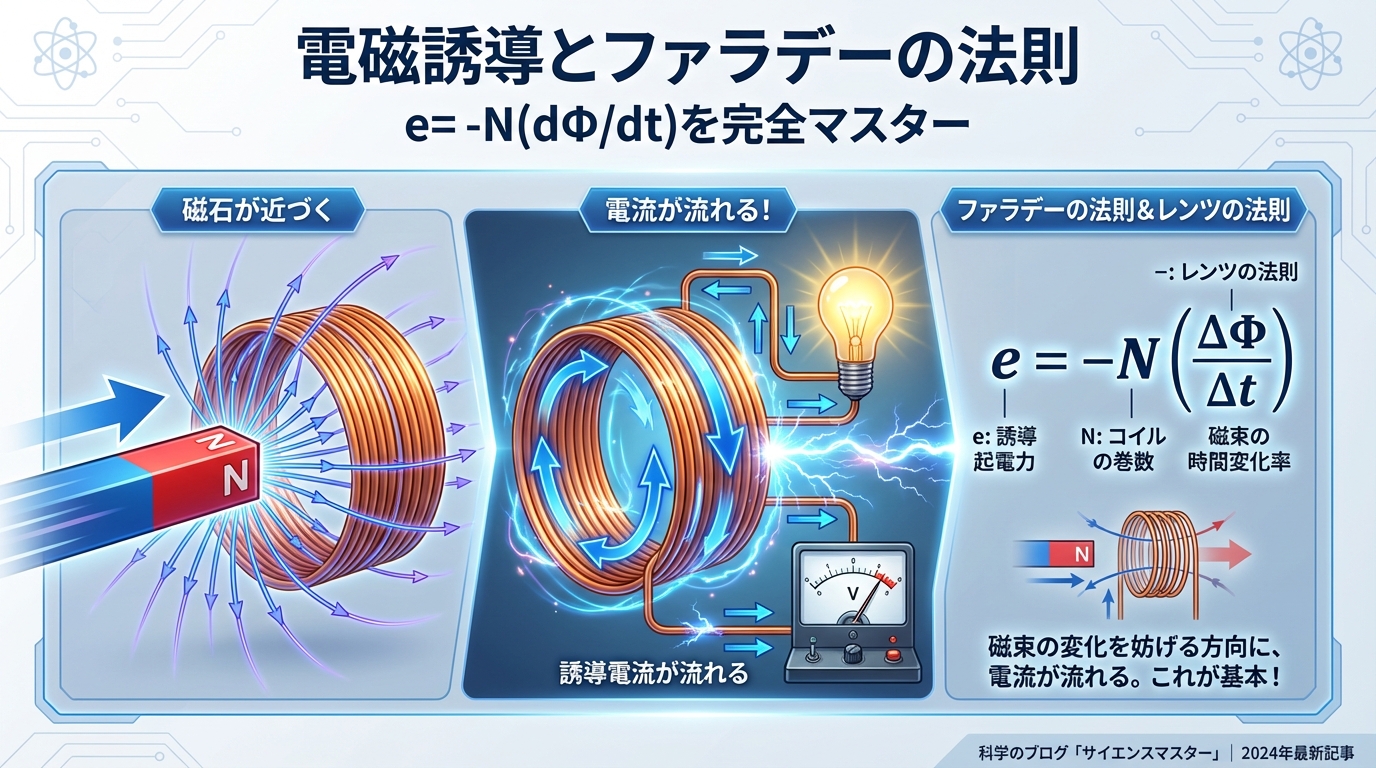
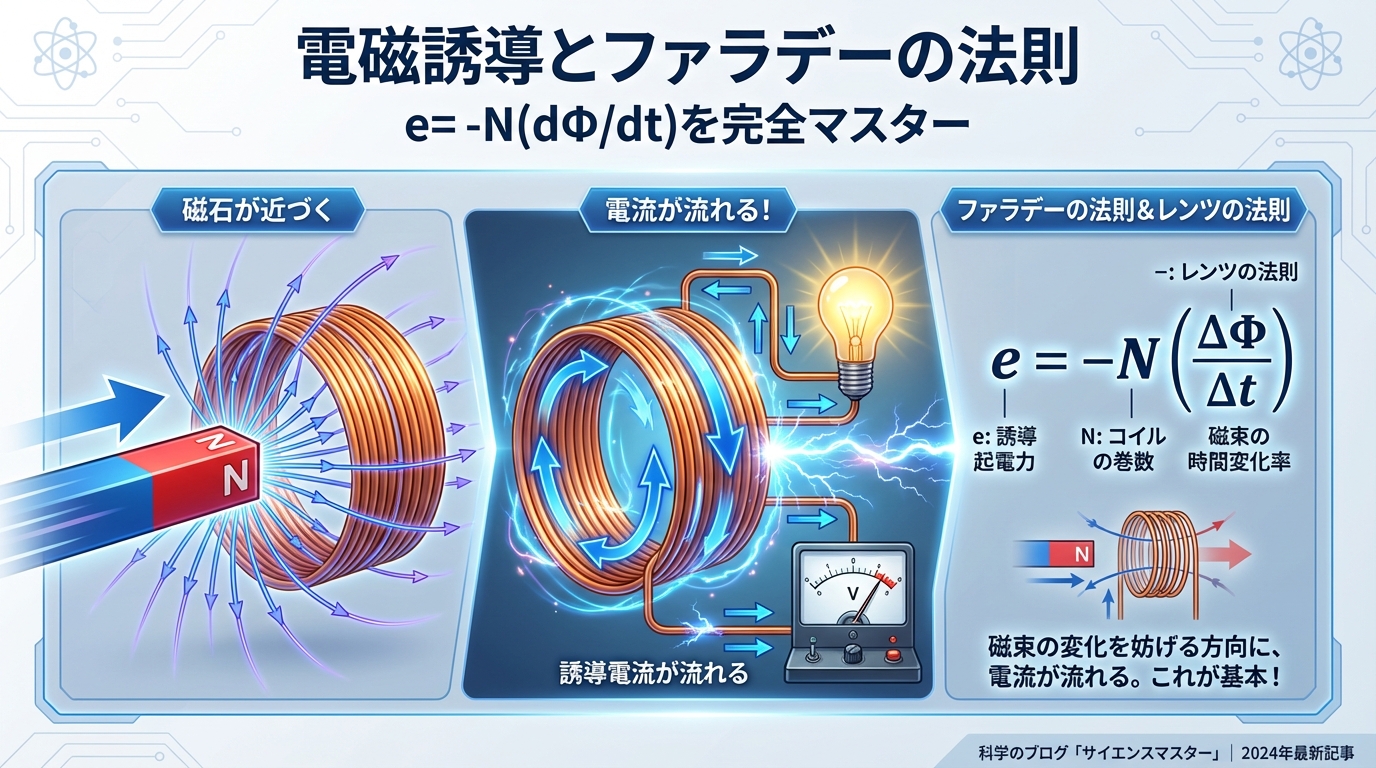
【電験三種・理論】電磁誘導とファラデーの法則|e=-N(dΦ/dt)を完全理解
2025/12/24 電磁誘導
「e=-N(dΦ/dt)って、何これ?」「電磁誘導って難しそう…」「このマイナス記号は何のため?」 そんな不安を抱えているあなたへ。電験三種で最重要テーマの一つ、電磁誘導とファラデーの法則を、今日こそ ...
-

-
二項確率紙の使い方|計算なし!グラフに点を打つだけで検定・推定ができるアナログ技術
2025/11/23 計数値の検定・推定
こんにちは、シラスです。 これまで、比率の検定や推定を行うために、複雑なルート($\sqrt{}$)の計算をしてきました。 しかし、PCも電卓もなかった時代、品質管理の先人たちは「定規と鉛筆だけ」でこ ...
-

-
HSS型HSPあるある50選|この矛盾、私だけじゃなかった
2025/12/24 HSS型HSP
「旅行に行きたい!」って思ったのに、出発前日に「やっぱり家にいたい…」って気持ちになる。 友達と遊ぶ約束をしたのに、当日になると「キャンセルしたい…でも楽しみ…でも疲れそう…」って葛藤する。 新しい趣 ...
-

-
独身の老後は誰が守るのか?HSPこそ今すぐ「新NISA」の設定を終わらせて、お金の不安を自動化せよ
2025/11/26
「このまま一生独身だったら、老後はどうなるんだろう?」 「会社が倒産したら? 病気になったら?」 HSP(繊細な人)は、未来のリスクを敏感に察知してしまうため、常に漠然とした不安を抱えています。 結婚 ...
-
-
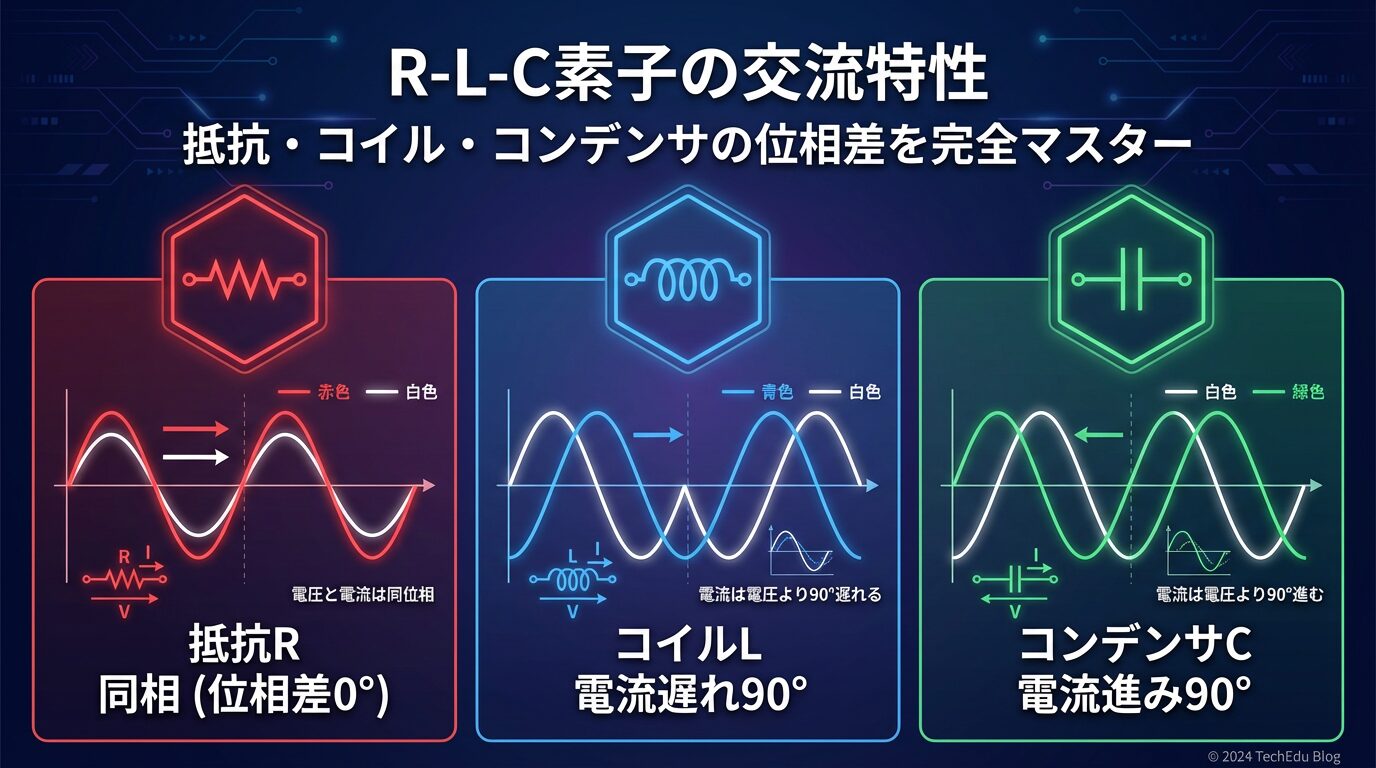
【電験三種・理論】R-L-C素子の性質|抵抗・コイル・コンデンサの交流特性
2025/12/23 交流回路
「コイルとコンデンサで、なぜ電流と電圧にズレが生じるんだろう…?」「抵抗だけ同相って、どういうこと?」 そんな疑問を抱えているあなたへ。電験三種の理論分野で最も重要なテーマの一つ、R-L-C素子の交流 ...
-

-
【電験三種・理論】瞬時値と位相|交流の式v=Vmsinωtを理解する
2025/12/23 交流回路
💡 こんな悩み、抱えていませんか? 「v = Vmsinωtって何?暗号にしか見えない…」 「瞬時値って聞くけど、イメージが全然わかない」 「位相差と初期位相…違いが混乱する!」 「公 ...
-

-
母比率の区間推定|テレビの視聴率や内閣支持率の「誤差±3%」はどう計算されているか?
2025/11/23 計数値の検定・推定
こんにちは、シラスです。 テレビのニュースや選挙速報を見ていると、画面の端っこにこんな小さな文字が表示されているのを見たことがありませんか? 「全国の有権者 1,000人 に電話調査を行いました」 こ ...
-

-
「何もできなかった休日を責めないで|HSPの自己肯定感を高める方法」
2025/12/14
「何もできなかった休日」を責めないで|HSPの自己肯定感を高める方法 日曜の夜。何もできなかった休日を振り返って、「今日も何もしなかった…」と自分を責めていませんか? 大丈夫です。あなたは悪くありませ ...
-

-
新年の抱負は書くな。「やらないことリスト」を10個決めろ。30代独身が捨てるべき無駄な習慣と人間関係
2025/11/26
「今年こそは、英語をマスターする」 「今年こそは、ジムに通う」 「今年こそは、副業で稼ぐ」 新年になると、誰もが輝かしい「抱負(To Do)」を掲げます。 しかし、断言します。その目標は、1ヶ月後には ...
-
-
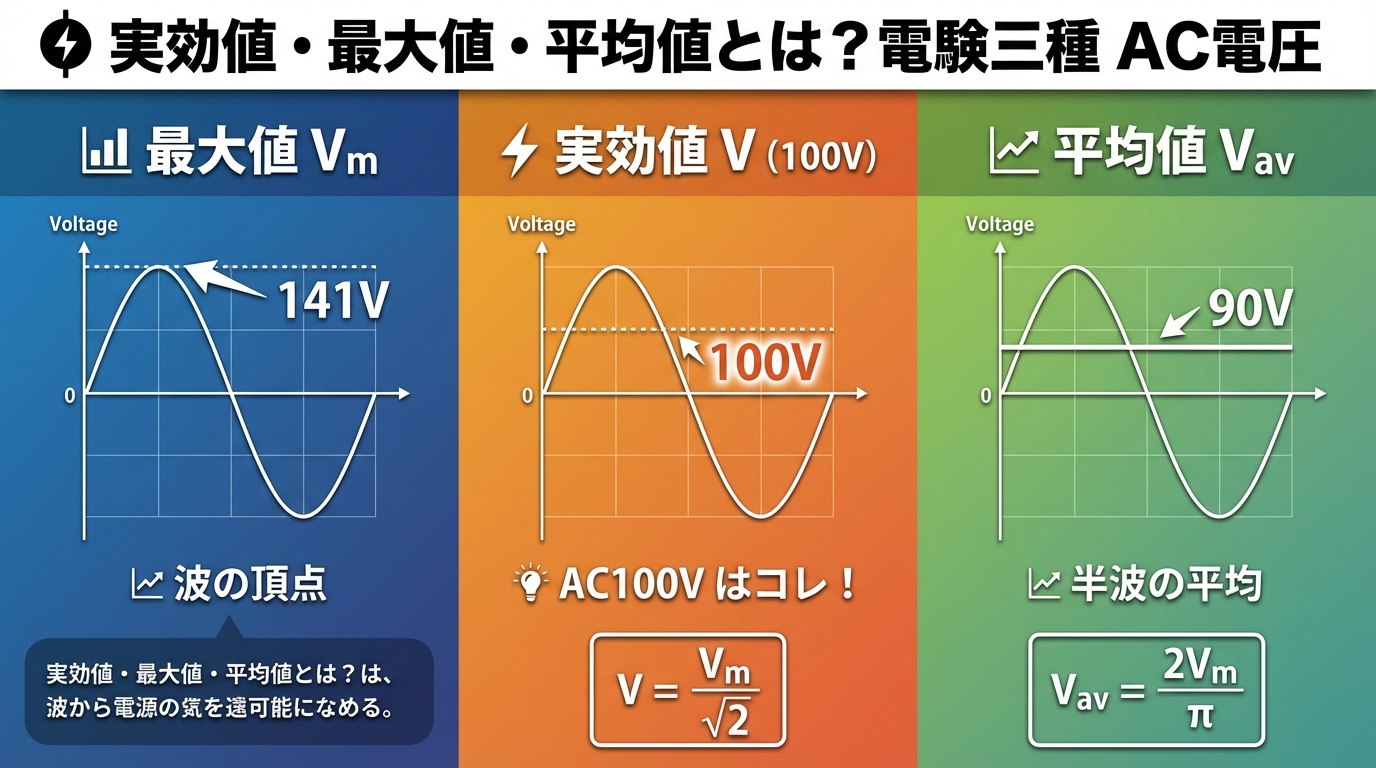
【電験三種・理論】実効値・最大値・平均値|なぜ100Vなのか?を完全理解
2025/12/22 交流回路
💡 こんな疑問を抱えていませんか? ✅ 「AC100Vって、実際は何ボルトなの?」 ✅ 「実効値・最大値・平均値…違いがよくわからない!」 ✅ ...