ホイートストンブリッジの原理│平衡条件と未知抵抗の測定方法

※本記事にはプロモーション（広告）が含まれています。

1️⃣ ホイートストンブリッジとは?

🔍 基本的な構成

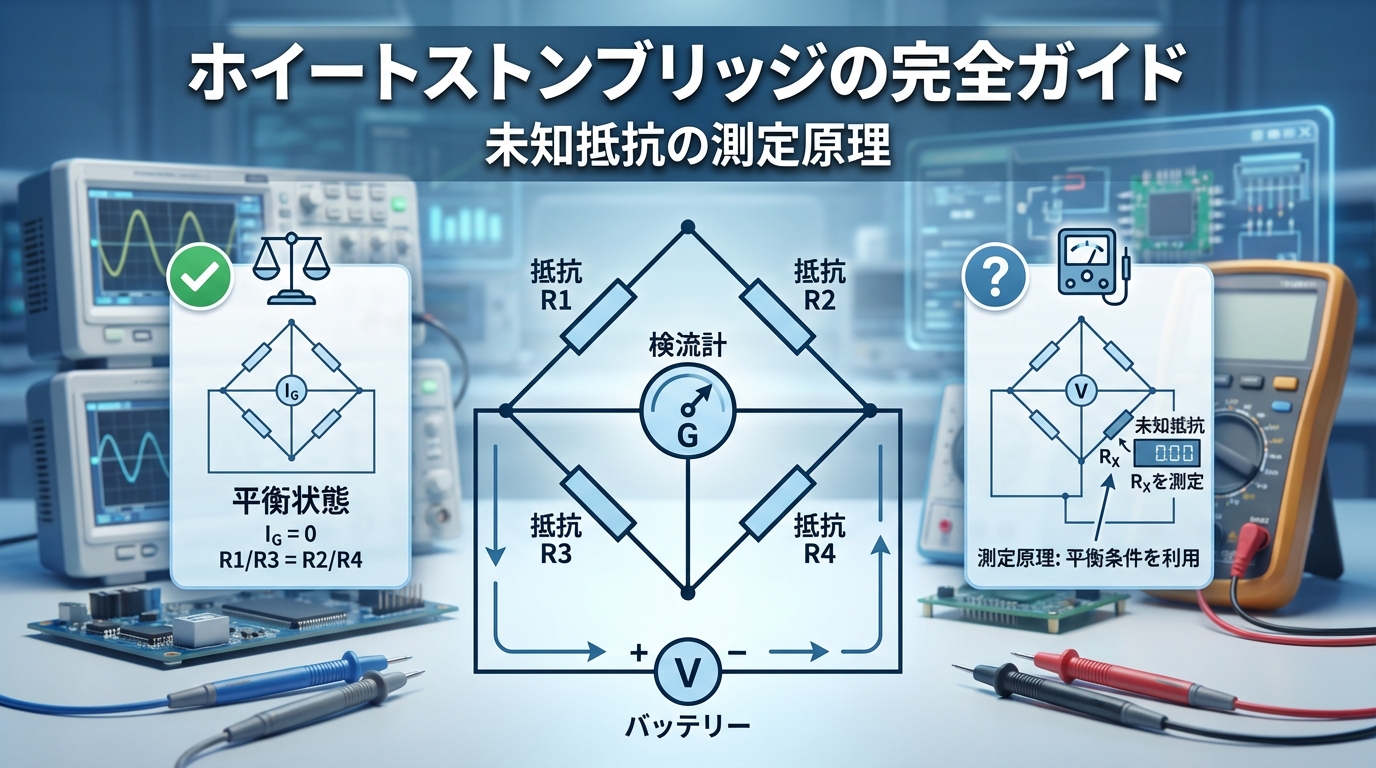
ホイートストンブリッジは、4つの抵抗をダイヤモンド型に配置した測定回路です。

📏 構成要素:
• 4つの抵抗(R1、R2、R3、R4)
• 電源(電池E)
• 検流計(ガルバノメータG)

🎯 目的: 未知の抵抗値を正確に測定する

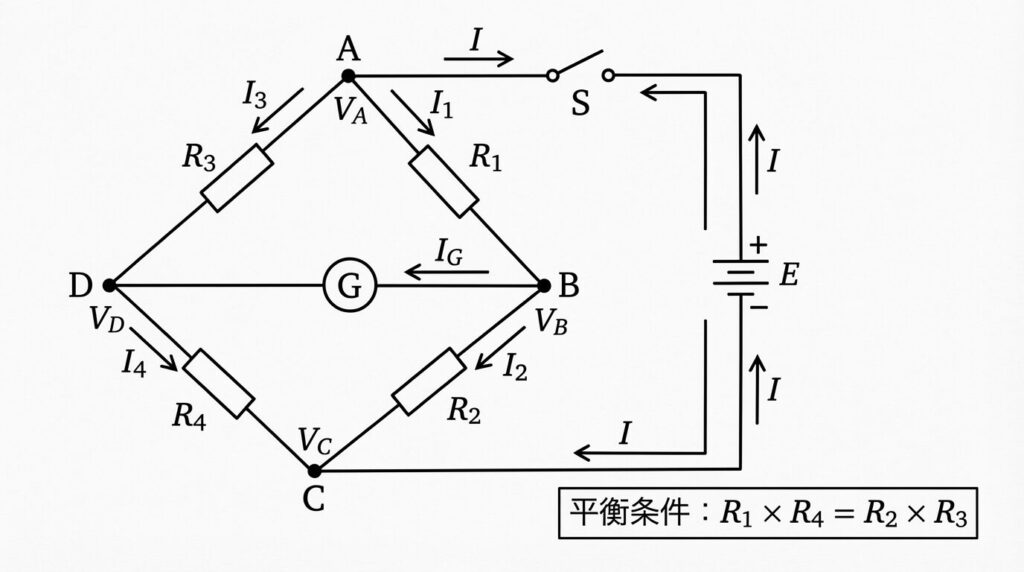
📐 回路図の読み方

ダイヤモンド型配置:
• 頂点A(上): 電源のプラス側
• 頂点B(右): R1とR2の接続点
• 頂点C(下): 電源のマイナス側
• 頂点D(左): R3とR4の接続点
• 中心: 検流計GがBとDを接続

検流計の電流IGがゼロになったとき、平衡状態!

🔗 関連記事:
📖 電験三種「理論」科目攻略法
📖 電験三種の公式暗記術
📖 統計の基礎知識

2️⃣ 平衡条件R1×R4 = R2×R3の証明

🧮 証明の流れ(超わかりやすく!)

平衡状態の定義:
検流計に電流が流れない(IG = 0)ということは、点Bと点Dの電位が等しいということです。

VB = VD (これが平衡の本質!)

📊 ステップ1:電圧降下を考える

右側の経路(A→B→C):
• 点Aから点Bへの電圧降下: V_AB = I1 × R1
• 点Bから点Cへの電圧降下: V_BC = I1 × R2
• 電源電圧E = I1 × (R1 + R2)

よって、点Bの電位VBは:

VB = E × R2 / (R1 + R2)

左側の経路(A→D→C):
• 点Aから点Dへの電圧降下: V_AD = I3 × R3
• 点Dから点Cへの電圧降下: V_DC = I3 × R4
• 電源電圧E = I3 × (R3 + R4)

よって、点Dの電位VDは:

VD = E × R4 / (R3 + R4)

🎯 ステップ2:平衡条件を導く

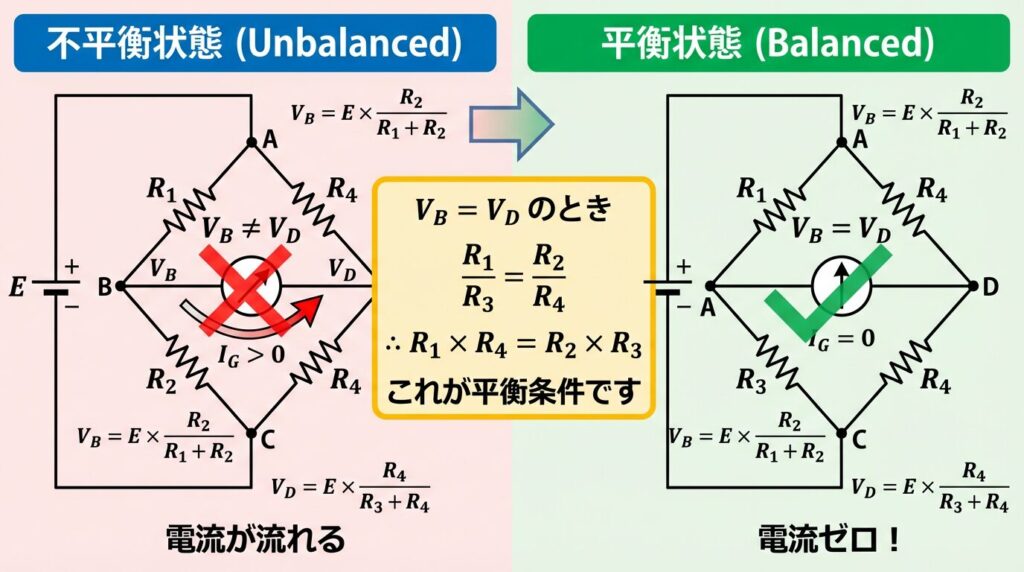
平衡状態では VB = VD なので:

E × R2 / (R1 + R2) = E × R4 / (R3 + R4)

両辺をEで割ると:
R2 / (R1 + R2) = R4 / (R3 + R4)

クロスして掛け算(外項の積 = 内項の積):
R2 × (R3 + R4) = R4 × (R1 + R2)

展開すると:
R2 × R3 + R2 × R4 = R4 × R1 + R4 × R2

R2 × R4を両辺から引くと:

R1 × R4 = R2 × R3

これが平衡条件です!

💡 覚え方のコツ:
• 「対角線の積が等しい」と覚えましょう!
• R1とR4は「対角」、R2とR3も「対角」
• ダイヤモンドの対角線をイメージすると忘れません!

別の表現:
R1/R3 = R2/R4 (比の形)も同じ意味です!

🔗 関連記事:
📖 電験三種「理論」科目の計算問題攻略法
📖 YouTubeで電験三種を制する独学インプット法
📖 統計学の基礎│品質管理への応用

3️⃣ 未知抵抗の測定方法(実験手順)

🔬 準備するもの

必要な機器:
• 未知抵抗 RX(測定したい抵抗)
• 標準抵抗 R1、R2、R3(値がわかっている抵抗)
• 可変抵抗(R3を微調整できるもの)
• 検流計(ガルバノメータ)
• 直流電源(乾電池でOK)
• 導線、スイッチ

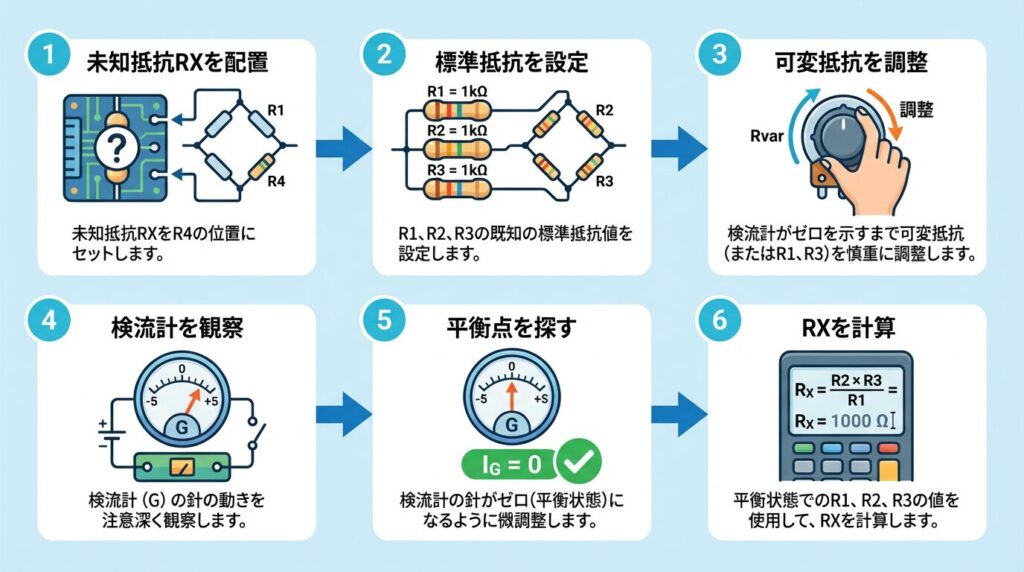
📝 測定手順(6ステップ)

ステップ1:回路を組む
• 未知抵抗RXをR4の位置に配置
• 他の3つの抵抗(R1、R2、R3)を配置
• 検流計を中央に接続
• 電源を接続

ステップ2:標準抵抗を設定
• R1とR2は固定値(例:R1=100Ω、R2=200Ω)
• R3は可変抵抗を使用(例:0~500Ωで調整可能)

ステップ3:電源を入れる
• 最初は検流計の針が振れる(不平衡状態)

ステップ4:可変抵抗R3を調整
• R3のつまみをゆっくり回す
• 検流計の針の動きを観察

ステップ5:平衡点を見つける
• 検流計の針がゼロになるポイントを探す
• IG = 0 になったら平衡状態!
• このときのR3の値を読み取る

ステップ6:RXを計算
• 平衡条件 R1 × RX = R2 × R3 を使う
• RX = (R2 × R3) / R1
• 計算して未知抵抗の値を求める!

📊 具体的な計算例

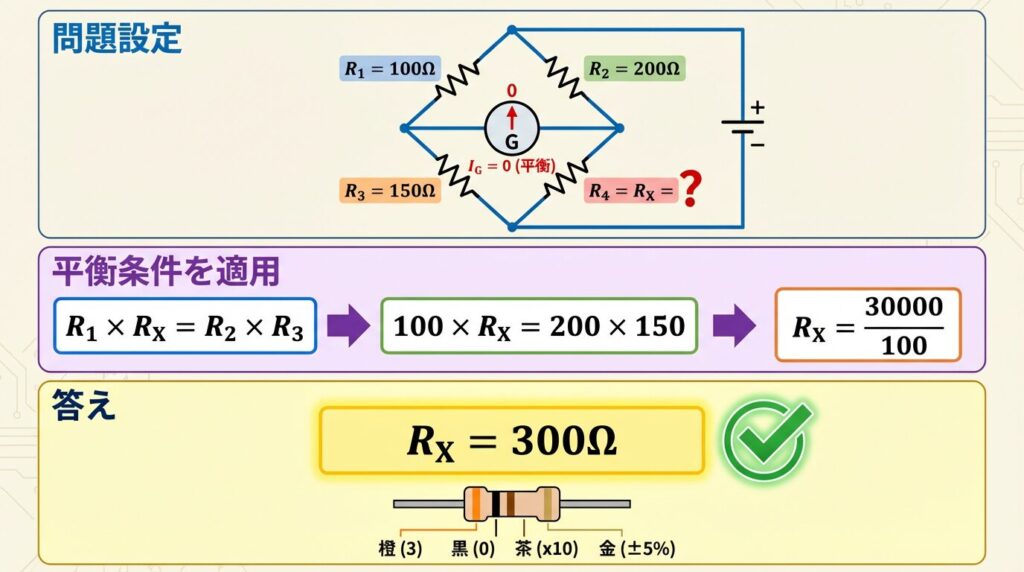
【例題】未知抵抗RXの測定

【条件】
• R1 = 100Ω(固定)
• R2 = 200Ω(固定)
• R3を調整して、R3 = 150Ωで平衡した
• RX = ?(求めたい値)

【解答】
平衡条件より:
R1 × RX = R2 × R3

RXについて解くと:
RX = (R2 × R3) / R1
RX = (200 × 150) / 100
RX = 30000 / 100

RX = 300Ω

答え:未知抵抗は300Ωです!

💡 実験のコツ:
• R3の調整はゆっくりと!(急に回すと平衡点を見逃す)
• 検流計の感度を最初は低くしておく(針が振り切れないように)
• 平衡点付近で感度を上げて精密調整
• R1とR2の比(R2/R1)を変えると測定範囲が変わる
• 例:R2/R1=2なら、RXはR3の2倍になる

🔗 関連記事:
📖 電験三種「理論」科目の頻出計算問題
📖 電験三種の公式暗記術
📖 電験三種とは?資格の全体像

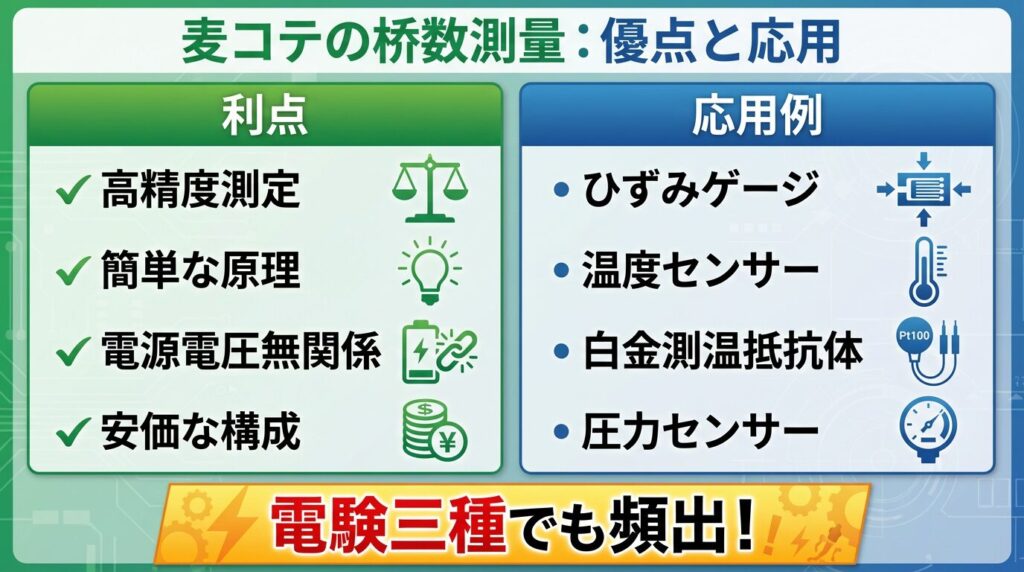
4️⃣ ホイートストンブリッジの利点と応用

✅ 4つの大きな利点

利点	理由
高精度測定	検流計のゼロ点を見るだけ(電圧計より正確)
電源電圧無関係	抵抗の比だけで決まる(電池が弱っても大丈夫)
簡単な原理	中学生でも理解できる電圧分圧の原理
安価な構成	抵抗と検流計だけで測定可能

🔧 実用的な応用例

応用分野	具体例	測定原理
ひずみゲージ	構造物の変形測定	変形で抵抗値が変化→平衡崩れを検出
温度センサー	白金測温抵抗体(Pt100)	温度で抵抗変化→微小変化を高精度検出
圧力センサー	圧力計、血圧計	圧力で抵抗変化→ブリッジ回路で測定
研究用途	微小抵抗の精密測定	標準抵抗との比較測定

📝 電験三種での出題パターン

頻出問題タイプ:

1. 未知抵抗の計算
「R1=〇Ω、R2=△Ω、R3=□Ωで平衡したとき、RXは?」
→ 公式 RX = (R2 × R3) / R1 を使う

2. 平衡条件の判定
「次の4つの抵抗値で平衡するか?」
→ R1×R4 = R2×R3 を確認

3. 応用問題
「ひずみゲージのブリッジ回路で…」
→ 抵抗変化量ΔRから不平衡電圧を求める

平衡条件の公式を覚えれば、ほぼ全問解けます!

🔗 関連記事:
📖 電験三種「電力」科目攻略
📖 電験三種「機械」科目攻略
📖 電験三種の合格率と難易度

📚 まとめ│ホイートストンブリッジの重要ポイント

🎯 この記事の重要ポイント

平衡条件はR1×R4 = R2×R3(対角線の積が等しい)
検流計がゼロ(IG=0)のときVB = VD(平衡状態)
未知抵抗はRX = (R2×R3)/R1で計算
電源電圧に関係なく高精度測定が可能
ひずみゲージ、温度センサーなど実用的な応用が多い
電験三種「理論」科目で頻出テーマ!

💪 次のステップ

初心者のあなたへ:
まずは「対角線の積が等しい」という覚え方で平衡条件を暗記しましょう!

電験三種受験者のあなたへ:
過去問で「未知抵抗の計算問題」を5問解いてみましょう。RX = (R2×R3)/R1 の公式を使えば即答できます!

実験をしたいあなたへ:
100円ショップの抵抗とテスターで簡易ブリッジ回路を作れます!実際に平衡点を探してみると理解が深まります!

🔗 あわせて読みたい関連記事

📖 電験三種「理論」科目の完全攻略ガイド
📖 独学者のための電験三種試験対策
📖 電験三種の公式暗記術
📖 電験三種とは?資格の全体像を解説
📖 30代未経験から電験三種で年収500万円を目指す方法
📖 統計学の基礎知識

この記事の理解を深める本と道具

おすすめの本

前後の単元とあわせて、教科書で体系立てて押さえておくと安心です。TAC出版『みんなが欲しかった！』シリーズの、電験三種「理論」の教科書と問題集が1冊になった本です。