📘 ガウスの法則、こんな悩みありませんか?
💡「ガウスの法則って何?名前からして難しそう…」
💡「∮E·dS = Q/ε₀って何の記号?意味が分からない…」
💡「どんな時にガウスの法則を使えばいいの?使い分けが分からない…」
✅ この記事で、すべてスッキリ解決します!
この記事では、「ガウスの法則」という電界計算の最強ツールを、「風船」や「シャワー」など身近な例え話を使って徹底的に解説します。
初心者の方でも、複雑な電界が簡単に計算できるようになります。
目次
ガウスの法則とは?ー 「閉じた面」を貫く電気力線を数える魔法
「ガウスの法則」は、電界を計算する上で最も強力なツールの一つです。
一見難しそうに見えますが、本質は驚くほどシンプルです。
🎈 風船の例えで理解するガウスの法則
ガウスの法則を理解する最も簡単な方法は、「風船」に例えることです。
🎈 風船の中の空気
想像してください。風船の中に空気を入れると、風船の表面は内側から押されますよね?
・空気が多い → 表面を押す力が大きい(風船が大きく膨らむ)
・空気が少ない → 表面を押す力が小さい(風船が小さい)
・空気がゼロ → 表面を押す力がない(風船が萎む)
重要:風船の外の空気は、風船を膨らませる力に関係ありません。
重要なのは「中の空気の量」だけです。
ガウスの法則も、これと全く同じです。
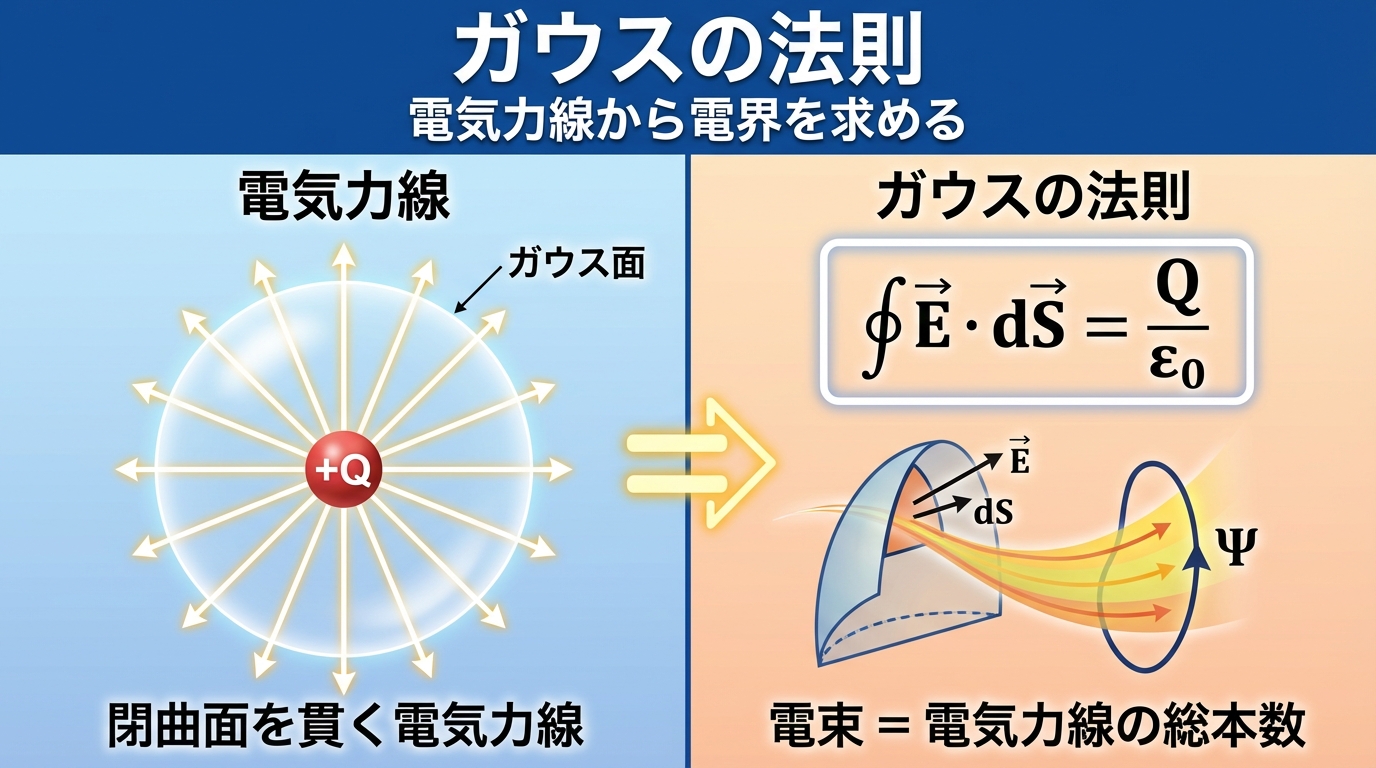
電荷のまわりには電気力線が出ていて、これを「閉じた面(風船の表面のようなもの)」で囲むと…
🎯 ガウスの法則の本質
✅ 閉曲面を貫く電気力線の総本数 = 閉曲面の中にある電荷の量 に比例する
✅ 閉曲面の外にある電荷は、貫く電気力線の総本数に影響しない
✅ つまり、「中の電荷を数えれば、表面を貫く電気力線の本数が分かる」
📐 ガウスの法則の公式
それでは、ガウスの法則を数式で表してみましょう。
⚡ ガウスの法則の公式
∮E·dS = Q / ε₀
∮:閉曲面全体で足し合わせる(積分記号)
E:電界の強さ [V/m]
dS:微小な面積 [m²]
Q:閉曲面内の電荷の総量 [C]
ε₀:真空の誘電率 = 8.85×10⁻¹² [F/m](定数)
または、電束Ψ(プサイ)を使って:
Ψ = Q / ε₀
この公式の意味を、もっと分かりやすく言い換えると…
💡 公式の意味(初心者向け)
閉曲面を貫く電気力線の総本数(左辺)
= 閉曲面の中の電荷の量(右辺)÷ ε₀
つまり、「袋の中の電荷を数えれば、袋を貫く電気力線の本数が分かる」ということです!
電束とは?ー 電気力線の「本数」を理解しよう
ガウスの法則を理解する上で、「電束(でんそく)」という概念が重要です。
これも、身近な例え話で理解していきましょう。
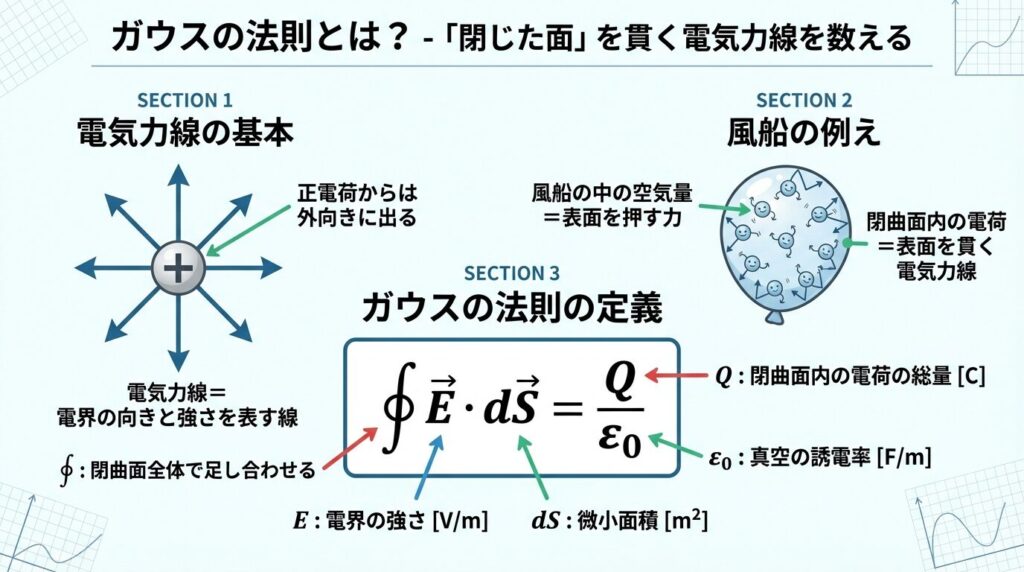
🚿 シャワーの例えで理解する電束
🚿 シャワーの水流
シャワーから出る水を想像してください。あなたは手のひらを水流にかざします。
ケース①:手のひらを水流に対して垂直に向ける
→ 手のひらに当たる水の量が最大(電束が最大)
ケース②:手のひらを斜めに傾ける
→ 手のひらに当たる水の量が減る(電束が減少)
ケース③:手のひらを水流に対して平行にする
→ 手のひらに当たる水の量がゼロ(電束ゼロ)
電束も、これと同じです。
電束とは、「面を貫く電気力線の本数」を表していて、面の向きによって変わります。
📌 電束の定義
電束 Ψ(プサイ):面を貫く電気力線の総本数
単位:[C](クーロン)または [N·m²/C]
公式:
Ψ = ∮E·dS = Q / ε₀
🔍 電束の重要な性質
📚 覚えておくべき3つの性質
性質①:電荷が閉曲面の外にある場合
Ψ = 0
理由:入る電気力線の本数 = 出る電気力線の本数 で、相殺される
性質②:電荷が閉曲面の中にある場合
Ψ = Q / ε₀
理由:電荷から出た電気力線は、すべて閉曲面を貫く
性質③:複数の電荷がある場合
Ψ = (Q₁ + Q₂ + Q₃ + ...) / ε₀
理由:閉曲面内の電荷の総和で決まる
💡 電束の覚え方
電束 = 電荷が「放つ」電気力線の総本数
※「束(そく)」という字は「本数をまとめたもの」という意味です
ガウスの法則の使い方ー 3ステップで電界を計算
ガウスの法則を使って電界を計算するには、3つのステップがあります。
この手順を覚えれば、複雑に見える問題もスッキリ解けるようになります。
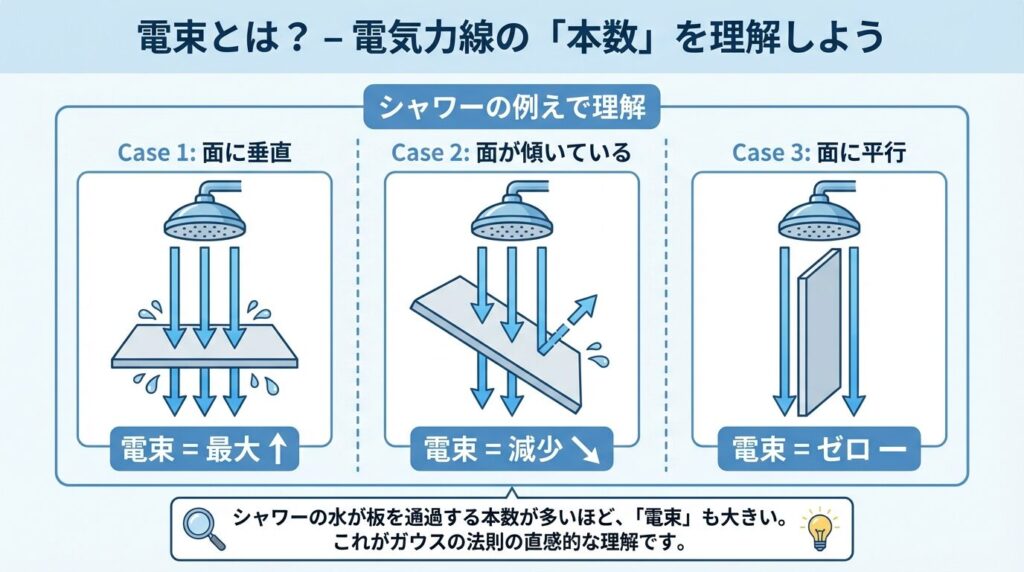
🔢 ガウスの法則・計算の3ステップ
STEP 1:対称性を見抜く
電荷の配置に「球対称」「円筒対称」「平面対称」のどれかがあるか確認
STEP 2:ガウス面を設定する
対称性に合わせて、球面・円筒面・直方体のいずれかを選ぶ
STEP 3:公式に代入して計算
E × (ガウス面の面積) = Q / ε₀ の形に整理して、Eを求める
⚠️ ガウスの法則が使える条件
ガウスの法則は万能ではありません。使える条件があります。
✅ ガウスの法則が使える条件
✓ 電荷の配置に対称性がある(球、円筒、平面など)
✓ ガウス面上で電界の強さが一定である
✓ 電界の向きがガウス面に対して垂直または平行
✓ 無限に広がる、または半無限の電荷分布
❌ ガウスの法則が使えない場合
✗ 対称性が全くない電荷配置(複雑な形状)
✗ ガウス面上で電界の強さがバラバラ
✗ 有限の大きさで、端の効果が無視できない場合
※ こういう場合は、クーロンの法則や電位を使って計算します
実践例①:点電荷のまわりの電界ー 球対称の場合
それでは、実際にガウスの法則を使って電界を計算してみましょう。
まずは最も基本的な「点電荷のまわりの電界」から始めます。
📚 例題①:点電荷の電界
問題:電荷Q [C] の点電荷があります。この電荷から距離r [m] 離れた点での電界の強さEを、ガウスの法則を使って求めてください。
【解答のステップ】
STEP 1:対称性を確認
点電荷は、どの方向から見ても同じ → 球対称
STEP 2:ガウス面を設定
球対称なので、半径rの球面をガウス面とする
球面の表面積 = 4πr²
STEP 3:ガウスの法則を適用
∮E·dS = Q / ε₀
球面上で電界Eは一定なので:
E × 4πr² = Q / ε₀
両辺を 4πr² で割ると:
E = Q / (4πε₀r²)
✅ 答え
E = Q / (4πε₀r²)
これは、クーロンの定数 k = 1/(4πε₀) = 9×10⁹ を使うと…
E = kQ / r²
これは、以前学んだ点電荷の電界の公式と全く同じですね!
💡 ポイント
ガウスの法則を使うと、積分計算なしで電界が求まります。
これが、ガウスの法則の「魔法」なんです!
実践例②③:線電荷と平面電荷ー 他の対称性の場合
📏 例②:無限に長い線電荷(円筒対称)
問題設定
無限に長い直線上に、単位長さあたりλ [C/m] の電荷が一様に分布しています。
この線から距離r [m] 離れた点の電界を求めます。
ガウス面の選び方:
線電荷を軸とする円筒面(半径r、高さL)を設定
円筒の側面積 = 2πrL
計算:
E × 2πrL = (λL) / ε₀
Lで割ると:
E = λ / (2πε₀r)
※ 電界は距離rに反比例します(点電荷のr²乗ではない!)
📐 例③:無限に広い平面電荷(平面対称)
問題設定
無限に広い平面上に、単位面積あたりσ [C/m²] の電荷が一様に分布しています。
この平面から離れた点の電界を求めます。
ガウス面の選び方:
平面を貫く直方体(底面積S)を設定
電界が通る面 = 2つの底面(上下)
計算:
E × 2S = (σS) / ε₀
Sで割ると:
E = σ / (2ε₀)
※ 驚くべきことに、電界は距離に依存しない(どこでも一定!)
📌 3つの対称性まとめ
球対称(点電荷):E ∝ 1/r²
円筒対称(線電荷):E ∝ 1/r
平面対称(面電荷):E = 一定(距離に無関係)
よくある間違いと電験三種の試験対策
⚠️ 初心者がやりがちな4つのミス
❌ ミス①:閉曲面の外の電荷まで含めてしまう
間違い:ガウス面の外にある電荷も Q に含めて計算してしまう
→ 正解:ガウス面の中にある電荷だけを数える。外の電荷は無関係!
❌ ミス②:ガウス面の形を間違える
間違い:対称性を無視して、適当な形のガウス面を選ぶ
→ 正解:球対称なら球面、円筒対称なら円筒面、平面対称なら直方体を選ぶ
❌ ミス③:面積計算を間違える
間違い:球の表面積を 4πr と間違える
→ 正解:球の表面積は 4πr²、円筒の側面積は 2πrL
❌ ミス④:対称性がない場合に無理やり使おうとする
間違い:複雑な形状なのに、ガウスの法則で解こうとする
→ 正解:対称性がない場合は、ガウスの法則は使えません。他の方法で解く
📝 電験三種での出題パターン
📚 頻出パターン
✅ 点電荷の電界 → 球対称、E=kQ/r² の導出
✅ 平行平板コンデンサの電界 → 平面対称、E=σ/(2ε₀) の応用
✅ 同心球導体の電界 → 球対称、中空部分と外部の電界
✅ 電束の計算 → Ψ=Q/ε₀ の直接計算
✅ ガウス面の選び方 → 対称性を見抜く問題
🎯 試験で使える覚え方・テクニック
💡 暗記のコツ
覚え方①:ガウスの法則 = 「袋の中の電荷を数える」
覚え方②:電束Ψ = 「プサイ(Ψ)の形が、電気力線を束ねた形」
覚え方③:対称性 = 「球・筒・板」の3パターンだけ
覚え方④:面積公式
・球面:4πr²(4パイ、rの2乗)
・円筒側面:2πrL(2パイ、rかけるL)
まとめー ガウスの法則で電界計算をマスターしよう!
この記事では、ガウスの法則について、基本の考え方から実践的な計算例まで徹底解説しました。
✅ この記事のポイント総まとめ
📌 ガウスの法則 = 閉曲面を貫く電気力線の本数 = 中の電荷 ÷ ε₀
📌 風船の例え = 中の空気量が、表面を押す力を決める
📌 電束Ψ = 電気力線の総本数。単位は[C]
📌 計算3ステップ = ①対称性を見抜く、②ガウス面設定、③公式に代入
📌 3つの対称性 = 球(E∝1/r²)、円筒(E∝1/r)、平面(E=一定)
📌 重要 = ガウス面の「外」の電荷は無関係!
ガウスの法則は、対称性さえあれば、複雑な積分なしで電界が一瞬で求まる「魔法の定理」です。
風船やシャワーなど、身近な例え話で本質を理解すれば、公式も自然と覚えられます。
📚 次のステップ
ガウスの法則をマスターしたら、次は「コンデンサの電界」や「静電エネルギー」に進みましょう。
ガウスの法則を使えば、これらも驚くほど簡単に理解できます。
また、「電界と電位」の記事も合わせて読むと、理解がさらに深まります。
それでは、ガウスの法則を武器に、電験三種の理論科目を攻略していきましょう! 💪✨
あなたの合格を心から応援しています!