「モデルの当てはまりを確かめるために残差を見ましょう」と聞いて、「それって“誤差”と同じじゃないの?」と感じたことはありませんか。
実はこの2つ、見ている世界が違うので混同すると理解が一気に難しくなります。この記事では
-
残差と誤差の違いをゼロから整理
-
数式よりイメージでつかむ残差の計算手順
-
残差を使ってモデルを磨く3つのチェックポイント
をやさしく解説します。
目次
残差と誤差のちがいを一枚で整理
| 残差 (Residual) | 誤差 (Error) | |
|---|---|---|
| 対象 | サンプル(手元のデータ) | 母集団(未知の真のモデル) |
| 定義 | 実測値 − 予測値 | 実測値 − 真の値 |
| 記号例 |
|
|
| 計算できる? | できる(データから算出) | できない(真の値が不明) |
| 主な用途 | 当てはまり診断・外れ値検出 | 理論モデルの前提・推定の基礎 |
ポイント
残差は「観測できるズレ」。
誤差は「理想の世界と現実のズレ」で、直接は測れない。
残差は誤差の“見える化”に相当し、解析後の健康診断に使う。
残差が生まれるまで:3ステップでイメージ
① 散布図を描く
気温(x)とアイス売上(y)の点をプロット。点の「雲」を観察し、右肩上がりかどうか感覚をつかみます。
② 回帰直線を引く
最小二乗法で直線
を求めます。ここまでが“モデル作り”。
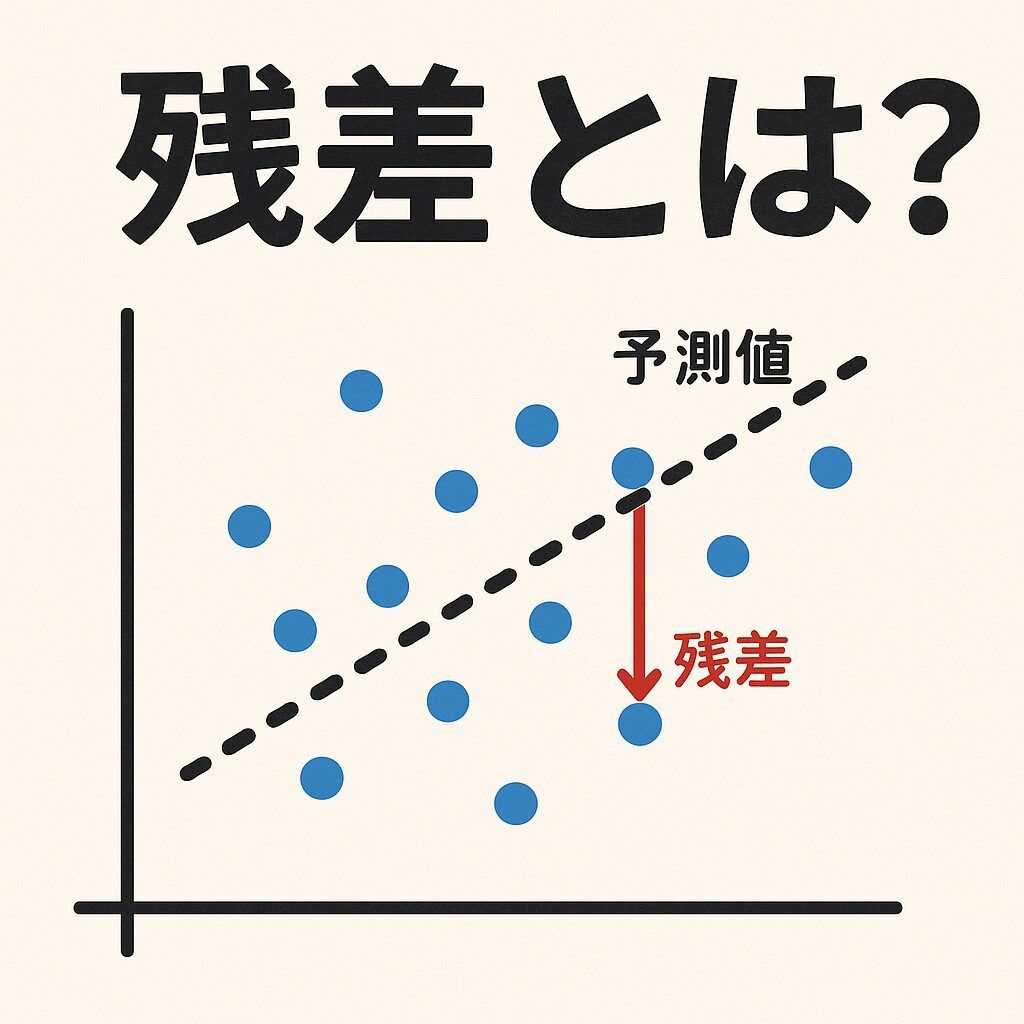
③ 残差を計算
各点について
を求めると、縦方向の短い矢印(画像参照)が残差。矢印が上下に散っていればモデルにまだ吸収しきれない要因が潜んでいる合図です。
残差が教えてくれる3つのこと
1. モデルの当てはまり
残差が上下にランダムなら「良い当てはまり」。もし右上がりにトレンドが残るなら、直線ではなく曲線モデルを検討します。
2. 外れ値・影響点の検出
ほかの点から大きく飛び出した残差は外れ値候補。クック距離などで影響の大きさを数値化し、必要ならデータ確認やロバスト回帰を行います。
3. 前提条件(誤差の仮定)の検証
回帰分析では「誤差は平均0・分散一定・独立・正規分布」という仮定を置きます。残差をヒストグラムやQQプロットで調べることで、誤差の仮定が破れていないかを推測できます。
よくある誤解と対処法
| 誤解 | なぜ起こる? | 正しい見方 |
|---|---|---|
| 残差=誤差だから深く考えなくていい | 用語が似ている | 残差は“見える”ズレ。分析後の品質チェックに必須 |
| 残差がゼロに近ければ完璧 | サンプルサイズが小さいと偶然でも小さく見える | 決定係数や交差検証も合わせて評価 |
| 外れ値は全部除去すべき | ルール化し過ぎ | ビジネス的に意味がある点なら残す判断も |
まとめ
-
残差は「データ」と「モデル予測」のズレを数値化した“健康診断レポート”。
-
誤差は未知の真のモデルとのズレで直接は測れないが、残差を通じて姿を推測できる。
-
残差をプロット・検定・外れ値チェックに活かすことで、モデルの説得力と予測精度が大幅アップ。