- 分散分析を勉強していたら、急に「E(V) = σ² + nσ²ₐ」という式が出てきた
- この「n」はどこから来たの?なぜ掛け算するの?
- 二元配置になると「br」とか「ar」とか、もう意味不明…
- 直交表や乱塊法では係数がまた違う。覚えられない!
- 過去問で「E(Vᵣ)を求めよ」と出てきて、何をすればいいかわからなかった
- E(V)の「本当の意味」を直感的に理解する
- 係数が「なぜその数字になるか」の統一ルール
- 一元配置から三元配置まで、すべて同じ考え方で解ける
- 直交表・乱塊法での係数の決め方
- E(V)がわかれば「F検定」の意味も完全理解できる
実験計画法やQC検定の勉強をしていると、突然現れる謎の概念「平均平方の期待値 E(V)」。
参考書を開けば、当たり前のように「E(Vₐ) = σ² + nσ²ₐ」なんて数式が出てきます。
でも正直、こう思いませんでしたか?
「え、この n ってどこから来たの?」
「なんで掛け算するの?」
「そもそも、これ何のために計算してるの?」
安心してください。ここでつまずくのはあなただけではありません。私もそうでした。
この記事では、数式の丸暗記は一切禁止。「どういう発想で作られているのか」をイメージで理解し、一元配置から乱塊法まで「全部同じルールで解ける」ことを体感してもらいます。
- E(V)とは、データの「中身(成分)」を分解して見せるレントゲン写真
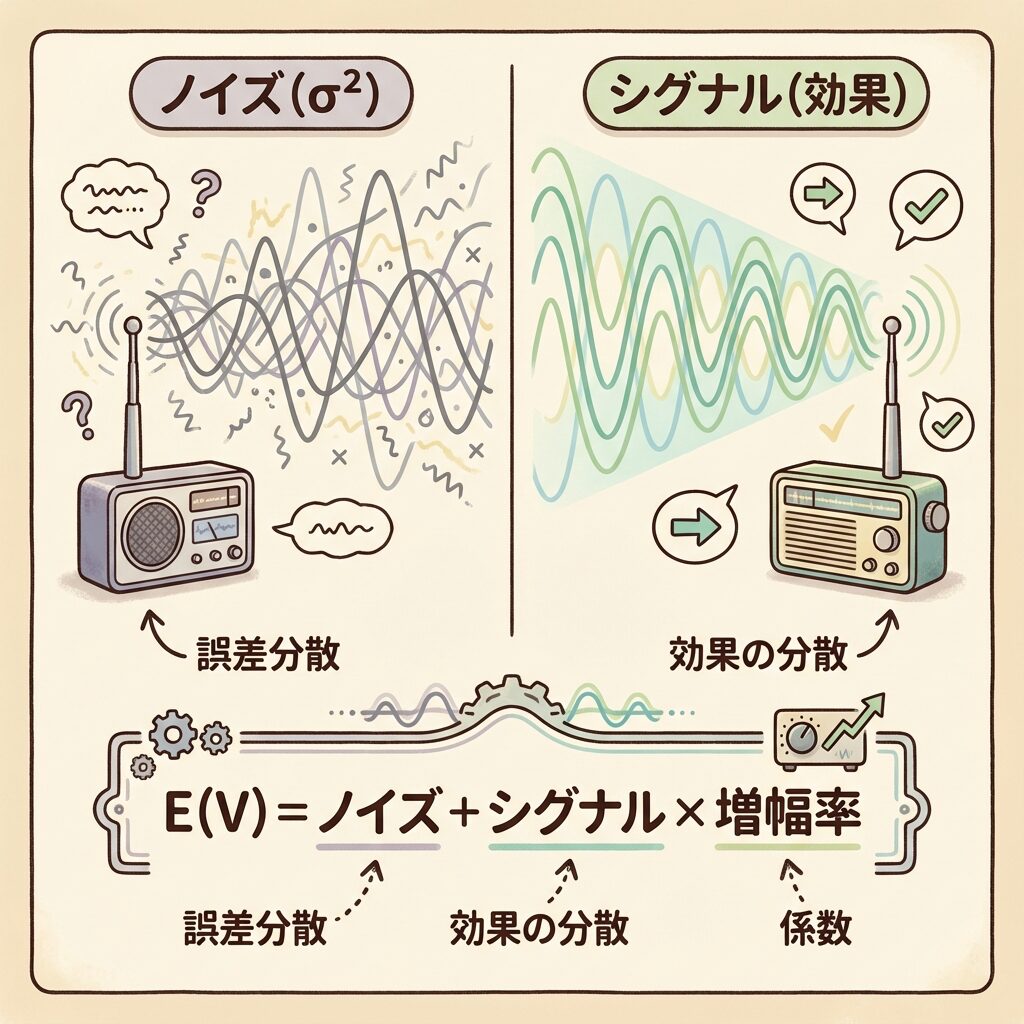
- 基本は「ノイズ(誤差σ²)」+「シグナル(効果)× 増幅率」
- 増幅率(係数)は「その要因の1水準に何個のデータがあるか」で決まる
- このルールさえ知れば、一元〜三元配置、直交表、乱塊法、すべて同じ考え方で解ける
目次
そもそも「平均平方の期待値 E(V)」とは何か?
まずは「E(V)とは何か」を、数式ではなくイメージで理解しましょう。
教科書的な定義
「もし同じ実験を無限回繰り返して平均をとったとき、その分散(V)が理論的にどんな値に落ち着くか」
…これだけだとイメージしづらいですよね。
もっとざっくり言うと、E(V)は「データの成分表」または「レントゲン写真」だと思ってください。
データは「シグナル」と「ノイズ」の混合物
実験で得られるデータは、常に2つの成分が混ざってできています。
🎵 シグナル(信号):聴きたい音楽や声=「要因の効果」
→ 温度を変えたら強度が変わった、という「意味のある変化」
📡 ノイズ(雑音):ザーザーという雑音=「偶然の誤差」
→ 同じ条件でも毎回少し違う、という「避けられないばらつき」
実験データを分析するとき、私たちは「このシグナルは本物か?それともただのノイズか?」を知りたいのです。
E(V)は、データの中に「シグナル」と「ノイズ」がどれくらいの割合で含まれているかを教えてくれるのです。
E(V)の基本形
これがE(V)のすべての基本形です。一元配置でも、三元配置でも、直交表でも、乱塊法でも、この形は変わりません。
変わるのは「係数」の部分だけ。そして、この係数には明確なルールがあるのです。
係数の決め方|たった1つの統一ルール
E(V)で最もつまずきやすいのが「なぜこの係数になるのか」という点です。
でも実は、係数の決め方にはたった1つのルールしかありません。
言い換えると:「その要因の効果を計算するとき、何個のデータを平均しているか」
このルールさえ覚えれば、一元配置から乱塊法まで、すべてのE(V)を自分で導き出せます。
なぜ「データの個数」を掛けるのか?
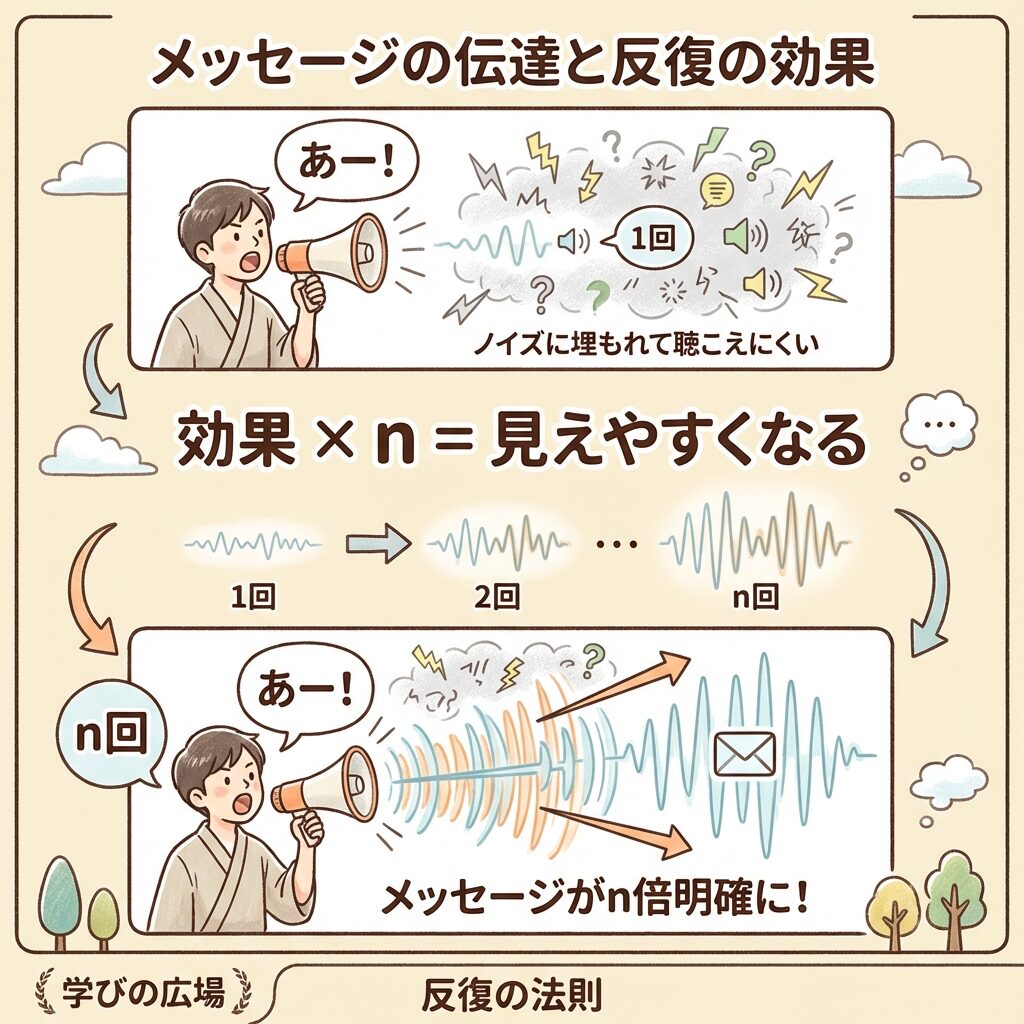
これを理解するために、「同じメッセージを繰り返し伝える」という比喩で考えてみましょう。
あなたは騒がしいパーティー会場で、友人の「田中さん」を呼ぼうとしています。
1回だけ「田中さん!」と叫ぶ場合:
→ 周りの雑音(ノイズ)にかき消されて、聞こえにくい
5回繰り返し「田中さん!田中さん!田中さん!田中さん!田中さん!」と叫ぶ場合:
→ 同じメッセージが5回届くので、雑音の中でも聞き取りやすくなる
→ 繰り返し回数が多いほど、「シグナル」が「ノイズ」に対して強くなる!
実験でも同じことが起きています。
同じ条件(同じ水準)でn回データを取ると、その条件の「効果」がn倍強調されて分散の中に現れるのです。
係数 = 増幅率 = その効果が何回分重なっているか
データが多いほど、効果(シグナル)はノイズに対して目立ちやすくなる。
その「目立ちやすさの倍率」が係数なのです。
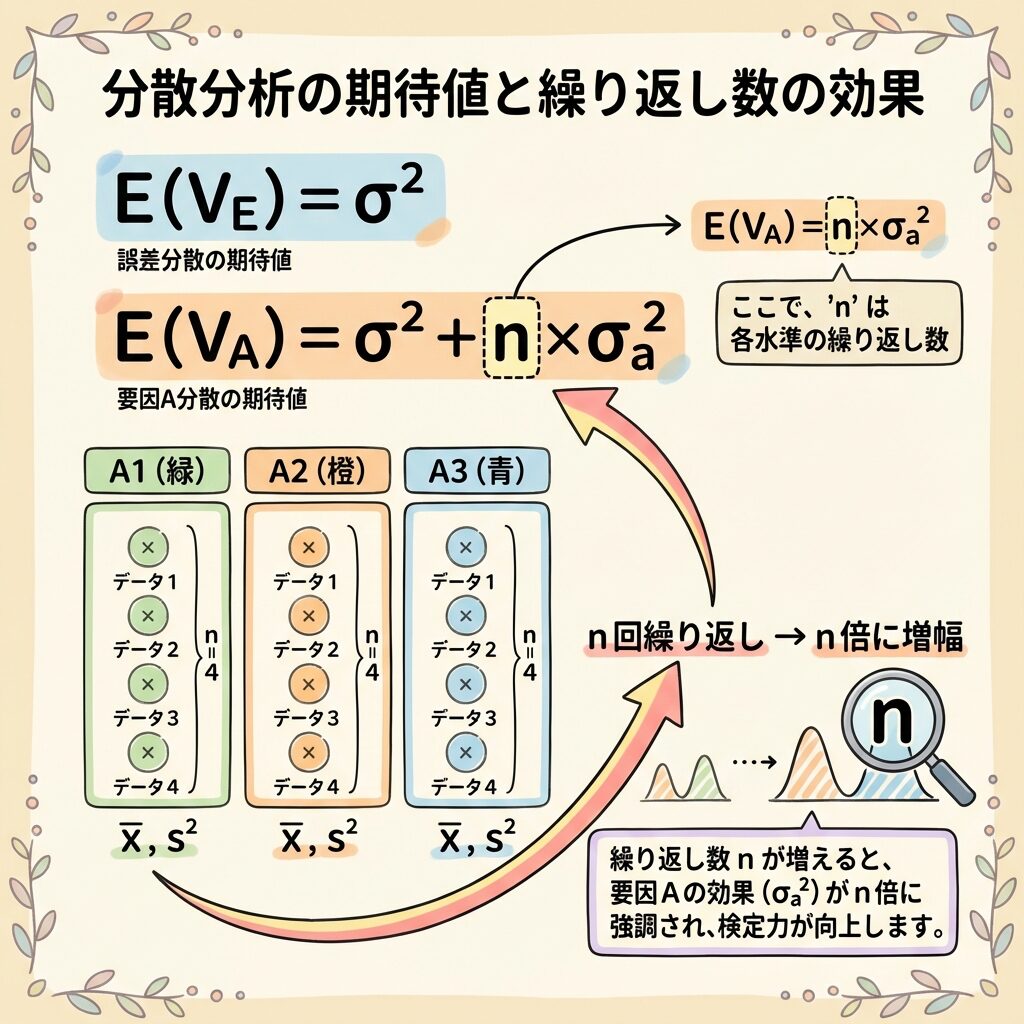
【一元配置実験】E(V)の基本を完全理解
まずは最もシンプルな「一元配置実験」でE(V)の考え方をマスターしましょう。
一元配置実験の設定
- 因子A:3水準(A₁, A₂, A₃)
- 繰り返し:各水準で4回ずつ実験
- 総データ数:3 × 4 = 12個
この実験のデータ構造を表にすると:
| 1回目 | 2回目 | 3回目 | 4回目 | データ数 | |
|---|---|---|---|---|---|
| A₁ | x₁₁ | x₁₂ | x₁₃ | x₁₄ | 4個 |
| A₂ | x₂₁ | x₂₂ | x₂₃ | x₂₄ | 4個 |
| A₃ | x₃₁ | x₃₂ | x₃₃ | x₃₄ | 4個 |
E(Vₑ):誤差分散の期待値
まず、誤差分散Vₑの期待値から考えます。
誤差は純粋な「ノイズ」だけで構成されているので、シグナル成分はゼロ。
だから、E(Vₑ)は単純にσ²(誤差の真の分散)になります。
E(Vₐ):因子Aの分散の期待値
次に、因子Aの分散Vₐの期待値を考えます。
ここで「統一ルール」を使います。
質問:因子Aの「1水準」に、何個のデータがあるか?
→ A₁には4個、A₂には4個、A₃には4個のデータがある
→ 答え:4個(= n = 繰り返し回数)
→ 係数は「4」!
σ²:どのデータにも含まれるノイズ
n × σ²ₐ:因子Aの効果が「n回分」増幅されたシグナル
A₁の平均を計算するとき、4個のデータを使います。
この4個のデータには、すべて「A₁の効果」が含まれています。
だから、A₁の効果は「4回分」積み重なって、分散の中で4倍に増幅されるのです。
一元配置実験とは?1つの因子で白黒つける実験の基本形 →
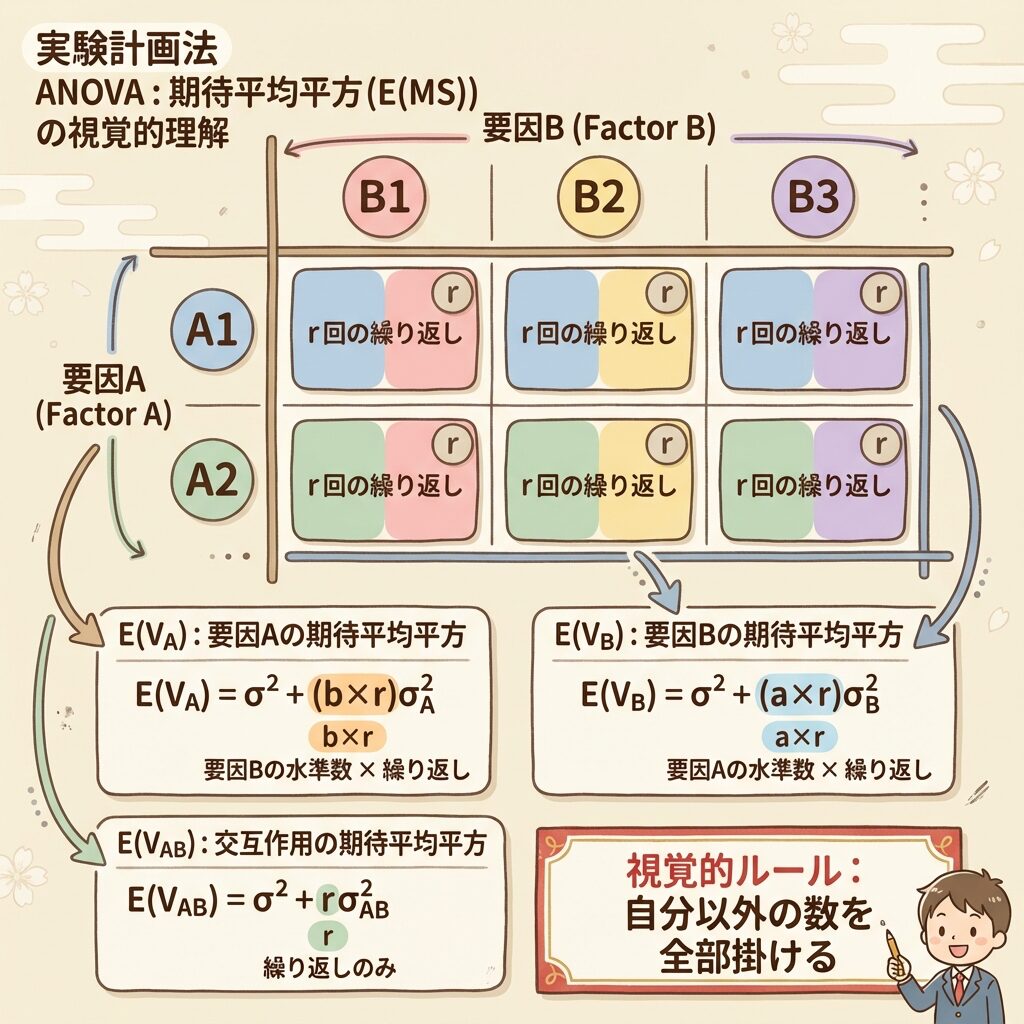
【二元配置実験】「自分以外を全部掛ける」ルール
要因が2つになる「二元配置実験」でも、基本は同じです。ただし、係数の計算が少し複雑になります。
ここで覚えてほしいのが「自分以外を全部掛ける」というルールです。
二元配置実験の設定
- 因子A:a = 2水準(A₁, A₂)
- 因子B:b = 3水準(B₁, B₂, B₃)
- 繰り返し:r = 2回
- 総データ数:2 × 3 × 2 = 12個
データ構造を表にすると:
| B₁ | B₂ | B₃ | Aの1水準の データ数 |
||||
|---|---|---|---|---|---|---|---|
| A₁ | x | x | x | x | x | x | 6個 (= b × r) |
| A₂ | x | x | x | x | x | x | 6個 (= b × r) |
| Bの1水準の データ数 |
4個 (= a × r) |
4個 (= a × r) |
4個 (= a × r) |
||||
「自分以外を全部掛ける」ルールの適用
各E(V)の係数を、統一ルールで求めてみましょう。
E(Vₐ):因子Aの期待値
質問:Aの「1水準」に何個のデータがあるか?
A₁には:B₁で2個 + B₂で2個 + B₃で2個 = 6個
これは b × r = 3 × 2 = 6 と計算できる
→ 係数は「b × r」!
E(V_B):因子Bの期待値
質問:Bの「1水準」に何個のデータがあるか?
B₁には:A₁で2個 + A₂で2個 = 4個
これは a × r = 2 × 2 = 4 と計算できる
→ 係数は「a × r」!
E(V_AB):交互作用の期待値
質問:交互作用A×Bの「1組み合わせ」に何個のデータがあるか?
A₁B₁の組み合わせには:繰り返し2回分 = 2個
これは r = 2 と計算できる
→ 係数は「r」!
よく見ると、係数は「自分以外の添字の積」になっています:
- E(Vₐ)の係数 → Aじゃない添字(bとr)の積 = b × r
- E(V_B)の係数 → Bじゃない添字(aとr)の積 = a × r
- E(V_AB)の係数 → AでもBでもない添字(r)だけ = r
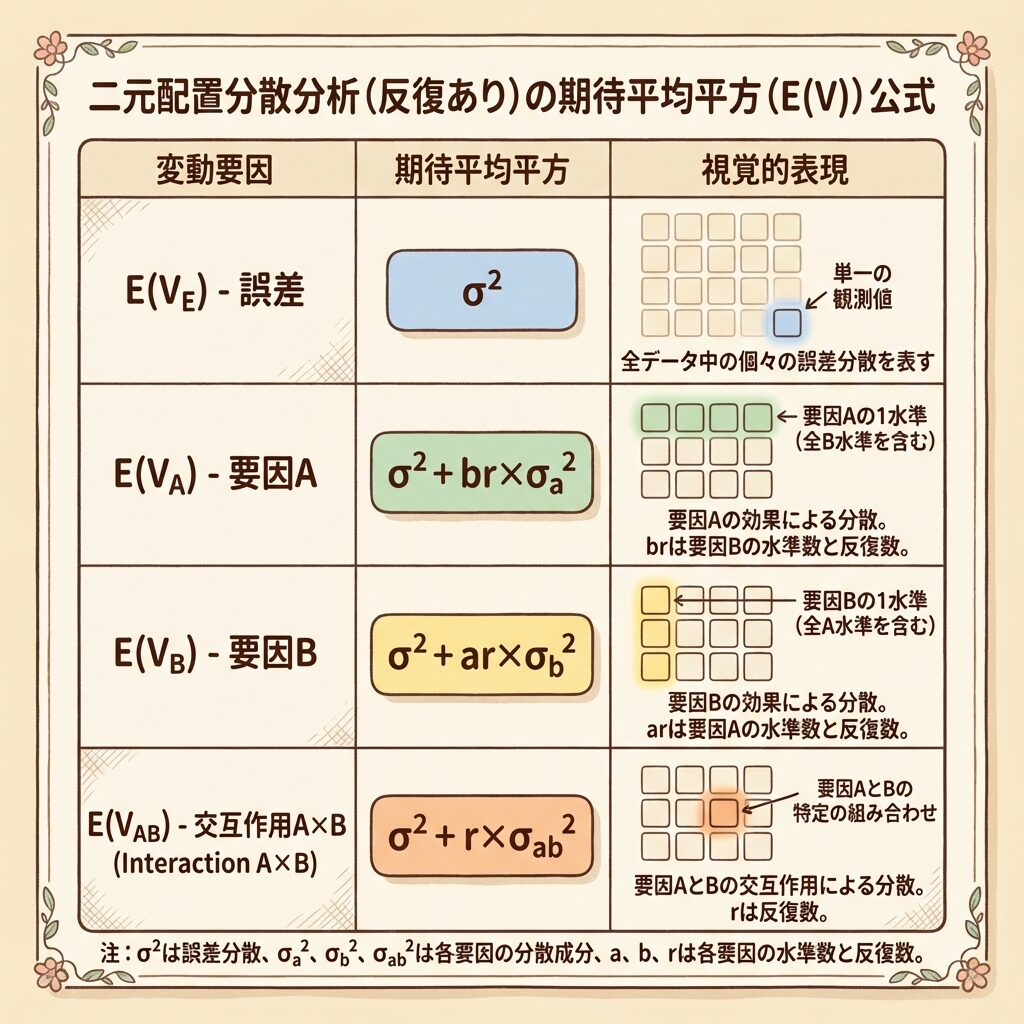
二元配置実験のE(V)一覧表
二元配置実験(繰り返しあり)のE(V)をまとめると:
| 要因 | E(V)の式 | 係数の意味 | この例での値 |
|---|---|---|---|
| A | σ² + br × σ²ₐ | Aの1水準のデータ数 | 3×2 = 6 |
| B | σ² + ar × σ²_b | Bの1水準のデータ数 | 2×2 = 4 |
| A×B | σ² + r × σ²_ab | A×Bの1組み合わせのデータ数 | 2 |
| E(誤差) | σ² | (係数なし) | − |
繰り返しなしの二元配置は?
繰り返しがない(r = 1)の場合、交互作用と誤差が分離できないため、E(V)の形が少し変わります。
| 要因 | E(V)の式(繰り返しなし) | 備考 |
|---|---|---|
| A | σ² + b × σ²ₐ | r=1なのでbだけ |
| B | σ² + a × σ²_b | r=1なのでaだけ |
| E(誤差) | σ² + σ²_ab | 交互作用が誤差に混入! |
繰り返しがないと、誤差のE(V)に交互作用σ²_abが混入します。これは「交互作用がないと仮定」しないとF検定ができないことを意味します。
【初心者向け】繰返しのない二元配置実験とは? →
【三元配置実験】同じルールで拡張できる
因子が3つになる「三元配置実験」でも、全く同じルールが適用できます。
三元配置実験の設定
- 因子A:a = 2水準
- 因子B:b = 3水準
- 因子C:c = 2水準
- 繰り返し:r = 2回
- 総データ数:2 × 3 × 2 × 2 = 24個
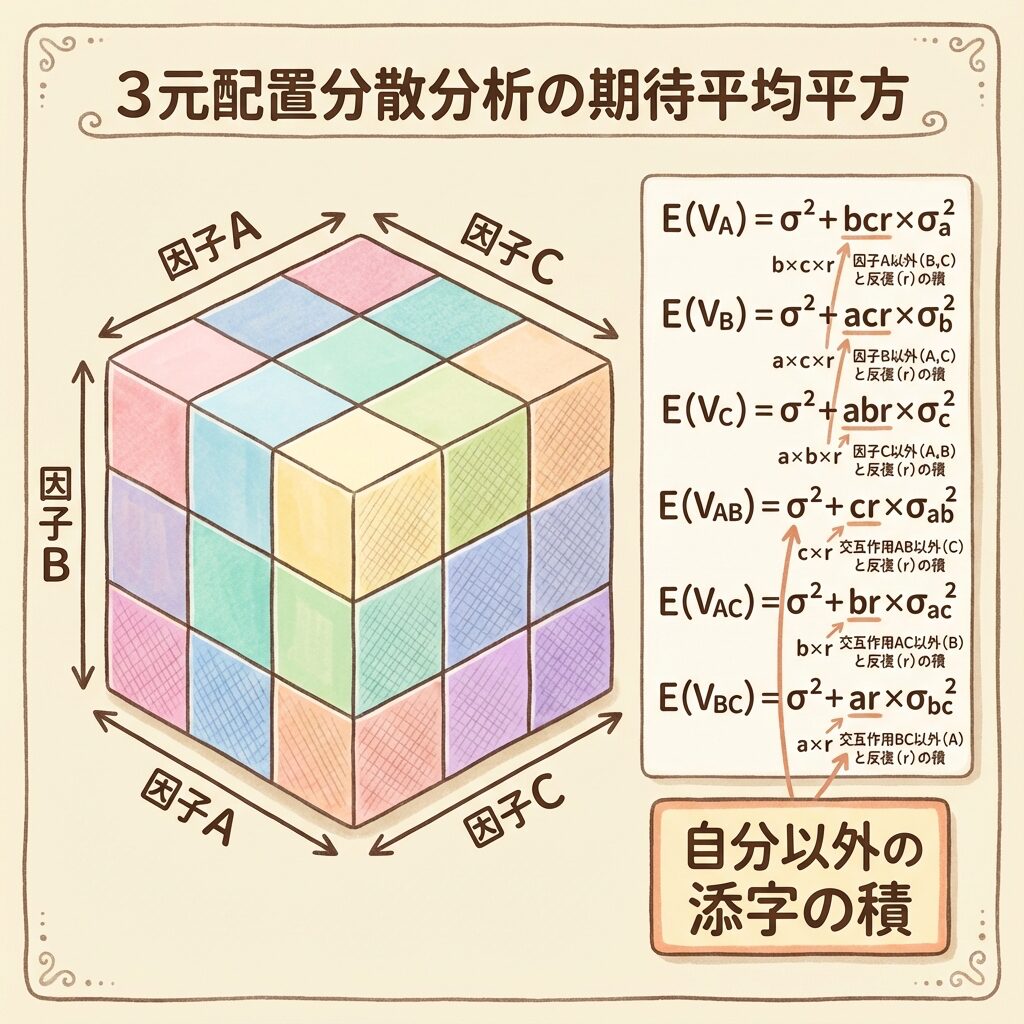
三元配置のE(V)一覧
| 要因 | E(V)の式 | 係数の計算 | この例での値 |
|---|---|---|---|
| A | σ² + bcr × σ²ₐ | Aの1水準のデータ数 | 3×2×2 = 12 |
| B | σ² + acr × σ²_b | Bの1水準のデータ数 | 2×2×2 = 8 |
| C | σ² + abr × σ²_c | Cの1水準のデータ数 | 2×3×2 = 12 |
| A×B | σ² + cr × σ²_ab | A×Bの1組み合わせのデータ数 | 2×2 = 4 |
| A×C | σ² + br × σ²_ac | A×Cの1組み合わせのデータ数 | 3×2 = 6 |
| B×C | σ² + ar × σ²_bc | B×Cの1組み合わせのデータ数 | 2×2 = 4 |
| A×B×C | σ² + r × σ²_abc | A×B×Cの1組み合わせのデータ数 | 2 |
| E(誤差) | σ² | − | − |
どの要因でも、係数は「自分以外の添字を全部掛け合わせたもの」になっています。
- Aの係数 → Aを除くb, c, rの積 = bcr
- A×Bの係数 → AとBを除くc, rの積 = cr
- A×B×Cの係数 → A, B, Cを除くrだけ = r
【直交表】実験回数が減っても同じ考え方
直交表を使った実験でも、E(V)の基本的な考え方は同じです。ただし、「全部の組み合わせを実験していない」点に注意が必要です。
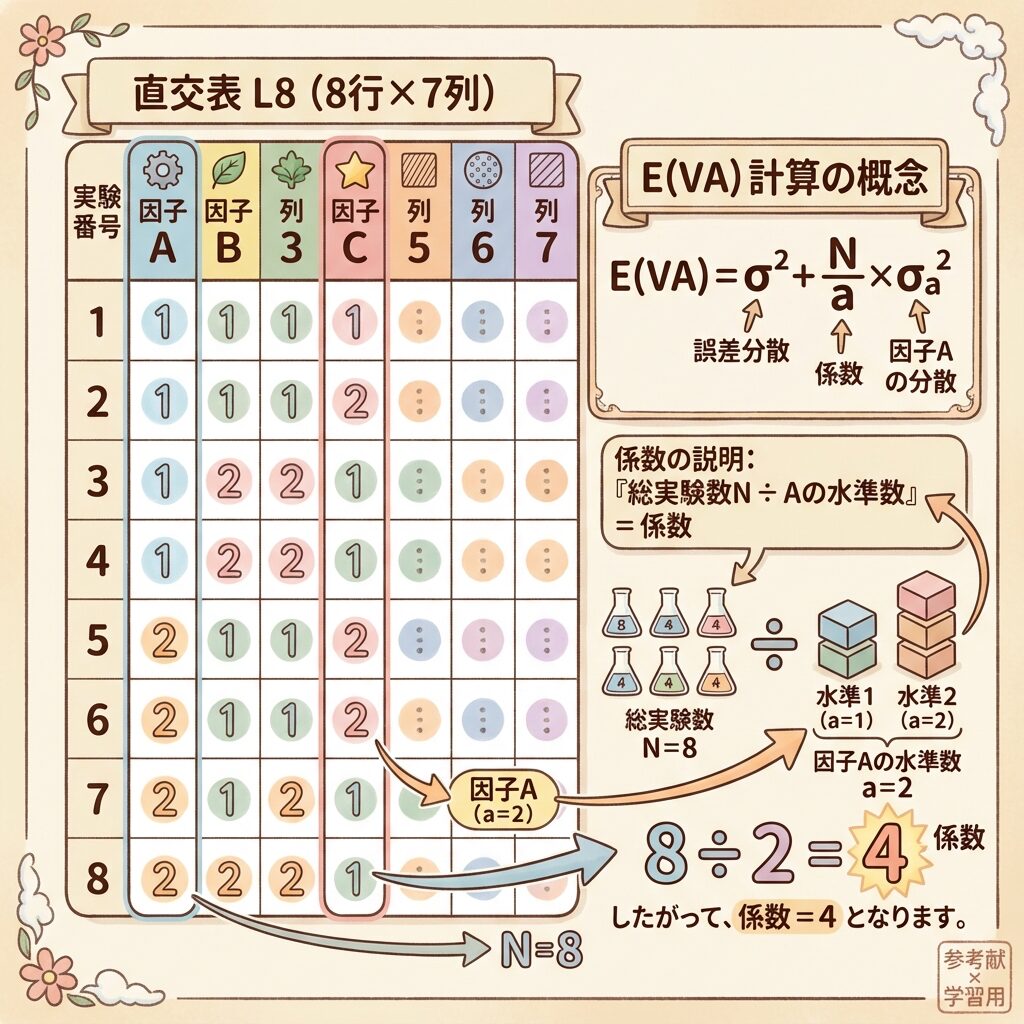
L8直交表の例
- 因子A, B, C, D:各2水準
- 実験回数:N = 8回(L8直交表使用)
- 繰り返し:なし(各条件1回ずつ)
L8直交表では、8回の実験で4因子を調べます。各因子には2水準あるので:
因子Aの1水準(A₁)に何個のデータがあるか?
→ 8回の実験のうち、A₁が使われるのは4回
→ これは N / a = 8 / 2 = 4 と計算できる
→ 係数は「N / a」!
直交表のE(V)公式
N:総実験回数
a:因子Aの水準数
N / a:Aの1水準に含まれるデータ数
L8直交表で因子A〜Dがすべて2水準の場合:
| 要因 | E(V)の式 | 係数 |
|---|---|---|
| A | σ² + 4σ²ₐ | 8/2 = 4 |
| B | σ² + 4σ²_b | 8/2 = 4 |
| C | σ² + 4σ²_c | 8/2 = 4 |
| D | σ² + 4σ²_d | 8/2 = 4 |
| E(誤差) | σ² | − |
直交表では、すべての因子が「バランスよく」配置されています。
だから、各因子のE(V)は同じ形になり、係数もすべて N/水準数 になります。
【乱塊法】ブロック因子のE(V)はここが違う
乱塊法では、ブロック因子RのE(V)が試験で頻出します。ここでも統一ルールが使えます。
乱塊法の設定
- 因子A:a = 2水準
- 因子B:b = 3水準
- ブロック因子R:r = 2水準(2日間)
- 総データ数:2 × 3 × 2 = 12個
- 繰り返し:なし(各ブロックで各組み合わせ1回)
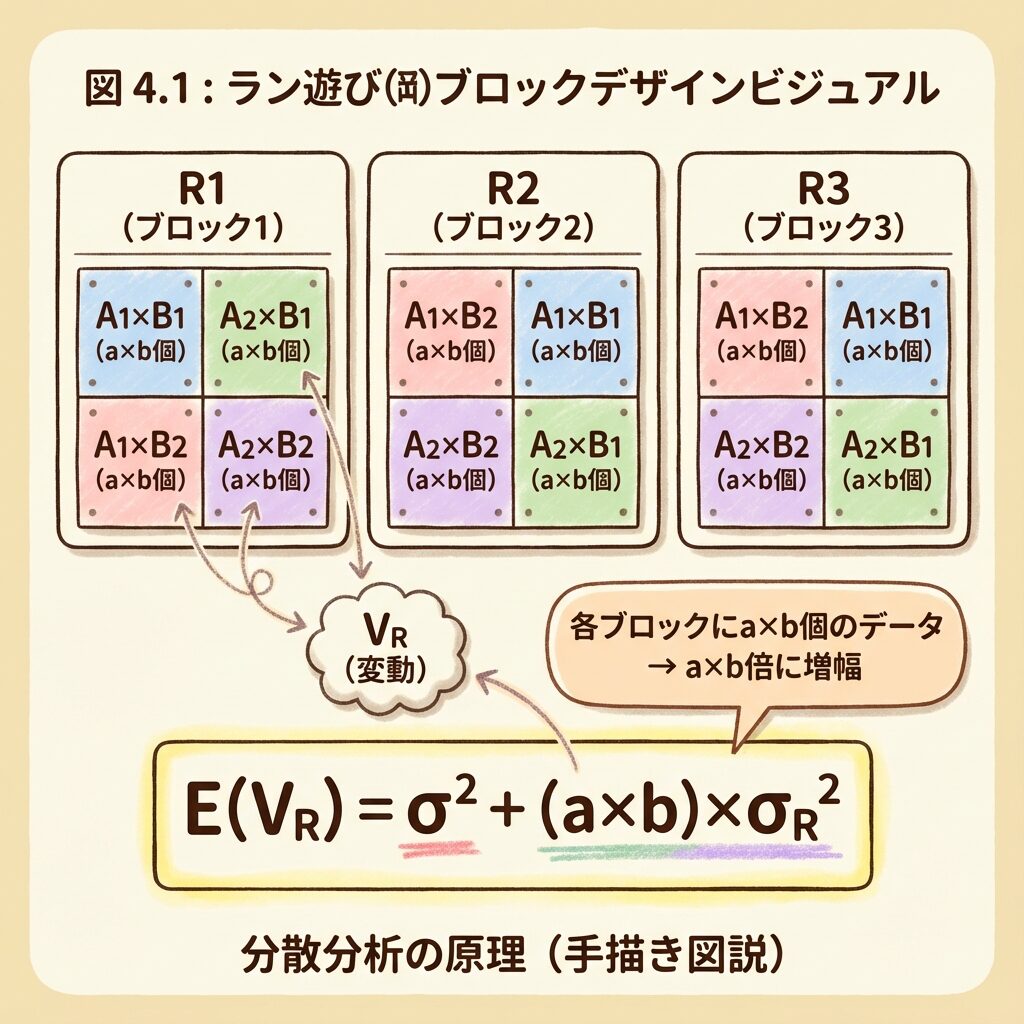
乱塊法の特徴は、各ブロック(各日)にすべてのA×Bの組み合わせが含まれることです。
| A₁B₁ | A₁B₂ | A₁B₃ | A₂B₁ | A₂B₂ | A₂B₃ | データ数 | |
|---|---|---|---|---|---|---|---|
| R₁(1日目) | x | x | x | x | x | x | 6個 (= a × b) |
| R₂(2日目) | x | x | x | x | x | x | 6個 (= a × b) |
ブロック因子RのE(V)
質問:ブロック因子Rの「1水準」に何個のデータがあるか?
→ R₁(1日目)には、A×Bのすべての組み合わせ = 6個
→ これは a × b = 2 × 3 = 6 と計算できる
→ 係数は「a × b」!
この例では:E(Vᵣ) = σ² + 6σ²ᵣ
乱塊法のE(V)一覧
| 要因 | E(V)の式 | 係数の意味 |
|---|---|---|
| R(ブロック) | σ² + ab × σ²ᵣ | Rの1水準のデータ数 = a × b |
| A | σ² + br × σ²ₐ | Aの1水準のデータ数 = b × r |
| B | σ² + ar × σ²_b | Bの1水準のデータ数 = a × r |
| A×B | σ² + r × σ²_ab | A×Bの1組み合わせのデータ数 = r |
| E(誤差) | σ² | − |
ブロック因子Rの係数が「a × b」になるのは、各ブロック(各日)にa×b個のデータが含まれるからです。1日目と2日目の「差」を見るとき、この6個分のデータが比較されるので、Rの効果は6倍に増幅されて現れます。
乱塊法とは?実験条件にばらつきがあるときの設計法 →
E(V)からブロック分散σ²ᵣを推定する
乱塊法の問題で頻出なのが、「ブロック因子の母分散σ²ᵣを推定せよ」という問題です。
E(V)の式を理解していれば、この問題は簡単に解けます。
σ²ᵣの推定公式の導出
E(Vᵣ)の式から、σ²ᵣを逆算します。
Step 1:E(Vᵣ)の式を書く
E(Vᵣ) = σ² + (a × b) × σ²ᵣ
Step 2:σ²ᵣについて解く
(a × b) × σ²ᵣ = E(Vᵣ) − σ²
σ²ᵣ = {E(Vᵣ) − σ²} / (a × b)
Step 3:期待値を実測値に置き換える
E(Vᵣ) → Vᵣ(分散分析表の値)
σ² → Vₑ(誤差分散)
計算例
- Vᵣ = 48.0(分散分析表から)
- Vₑ = 2.0(分散分析表から)
- 因子Aの水準数 a = 2
- 因子Bの水準数 b = 3
σ̂²ᵣ = (Vᵣ − Vₑ) / (a × b)
= (48.0 − 2.0) / (2 × 3)
= 46.0 / 6
= 7.67
日間変動(ブロック因子R)の母分散は約7.67と推定されます。
これは「日によって、標準偏差で約±2.8(= √7.67)程度のばらつきがある」ことを意味します。
E(V)がわかれば「F検定」の意味がわかる
最後に、E(V)を学ぶことで「なぜF検定をするのか」が理解できることを確認しましょう。
F値の計算を「中身」で見る
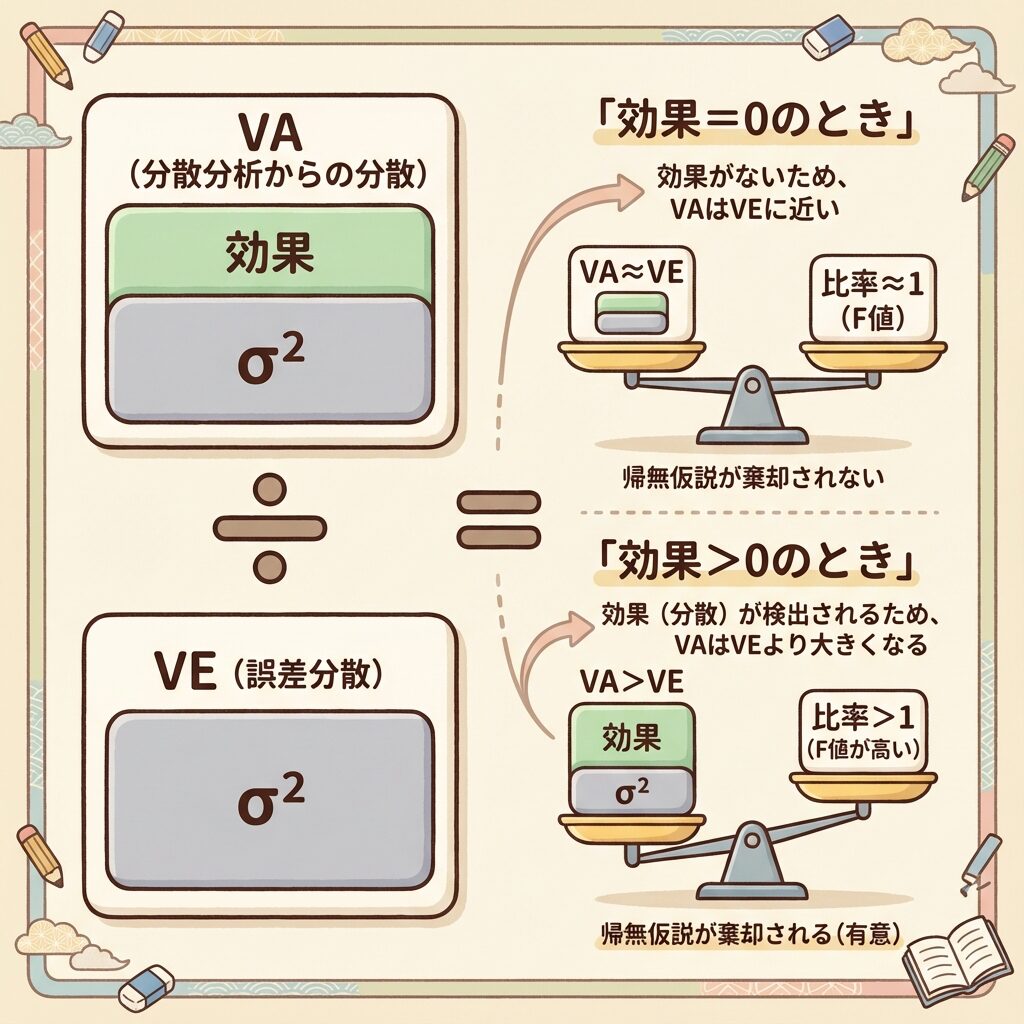
分散分析でF値を計算するとき、私たちは「Vₐ ÷ Vₑ」という割り算をしています。
この割り算の「中身」をE(V)で見てみましょう。
σ² + n × σ²ₐ
(ノイズ + シグナル)
σ²
(ノイズのみ)
ケース1:因子Aに効果がない場合(σ²ₐ = 0)
F = (σ² + 0) / σ² = σ² / σ² ≈ 1
→ F値は1に近くなる(分子と分母がほぼ同じ)
ケース2:因子Aに効果がある場合(σ²ₐ > 0)
F = (σ² + n × σ²ₐ) / σ² = 1 + n × (σ²ₐ / σ²) > 1
→ F値は1より大きくなる(分子が分母より大きい)
F検定とは、「分子のシグナル成分がゼロかどうか」を確かめる検定です。
- F ≈ 1 → シグナルがない(効果なし)
- F >> 1 → シグナルがある(効果あり)
E(V)の式を知っていることは、「何を何で割れば正しい検定ができるか」を知っていることと同じなのです。
F検定で有意差を判定する|F分布表の使い方 →
【保存版】E(V)の公式一覧表
この記事で解説したE(V)の公式を、一覧表にまとめます。試験直前の確認用にご活用ください。
統一ルール(これだけ覚えれば全部導ける)
実験タイプ別一覧
一元配置実験(因子A:a水準、繰り返しn回)
| E(Vₐ) | σ² + n × σ²ₐ |
| E(Vₑ) | σ² |
二元配置実験(繰り返しあり:因子A a水準、因子B b水準、繰り返しr回)
| E(Vₐ) | σ² + br × σ²ₐ |
| E(V_B) | σ² + ar × σ²_b |
| E(V_AB) | σ² + r × σ²_ab |
| E(Vₑ) | σ² |
直交表(総実験回数N、各因子k水準)
| E(V因子) | σ² + (N/k) × σ²因子 |
| E(Vₑ) | σ² |
乱塊法(因子A a水準、因子B b水準、ブロックR r水準)
| E(Vᵣ) | σ² + ab × σ²ᵣ ← 頻出! |
| E(Vₐ) | σ² + br × σ²ₐ |
| E(V_B) | σ² + ar × σ²_b |
| E(V_AB) | σ² + r × σ²_ab |
| E(Vₑ) | σ² |
分散推定の逆算公式
| 一般形 | σ̂²要因 = (V要因 − Vₑ) / 係数 |
| 乱塊法のσ̂²ᵣ | σ̂²ᵣ = (Vᵣ − Vₑ) / (a × b) |
