こんにちは、シラスです。
前回の記事で、1つの機械のバラつきを判定する「カイ二乗検定」を行いました。
その際、判定基準となる「カイ二乗分布表」を見て、違和感を覚えませんでしたか?
「正規分布(t検定など)のときは、右側が $+1.96$ なら、左側は $-1.96$ だったよね?
なんでカイ二乗検定は、右側(16.92)と左側(3.33)で、全然違う数字になるの?」
実は、これこそが「バラつき(分散)」を扱うときに避けて通れない「非対称性の罠」なのです。
今日は、なぜこんな歪んだ形になるのか、その理由を直感的に解説します。
1. 正規分布 vs カイ二乗分布
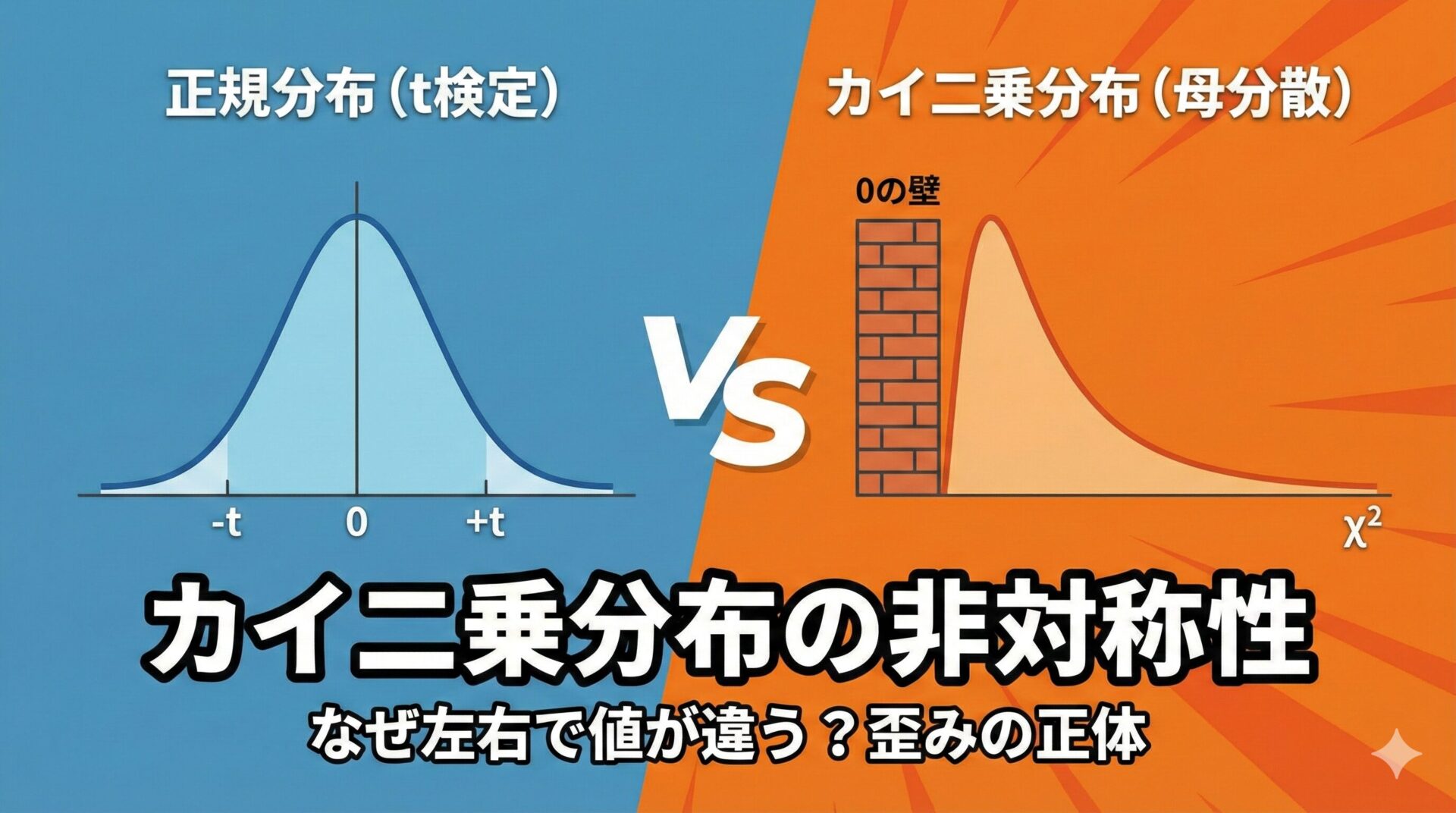
百聞は一見にしかず。まずは実際の分布の形を見てみましょう。

- 正規分布: 平均値(0)を中心に、左右対称の美しい釣鐘型です。
- カイ二乗分布(上図): 「0」の壁にぶつかって、左側が絶壁になり、右側にだけなだらかに伸びています。
なぜ、こんな形になるのでしょうか?
理由は、カイ二乗検定が「二乗(平方)」の世界の話だからです。
2. 理由A:左側に「0の壁」があるから
分散(バラつき)を計算するとき、私たちは必ず「二乗」をします。
マイナスの値を二乗するとプラスになりますよね?
つまり、バラつきの世界には「マイナス」が存在しません。
- どんなにバラつきが小さくても、最小値は「0」です。
- 正規分布のように「マイナス側」に広がることができず、左側に「0という鉄壁」が存在します。
だから、分布の左側はスパッと断ち切られたような形になるのです。
3. 理由B:右側は「暴走」するから
一方で、右側(プラス方向)には制限がありません。
しかも、「二乗」という計算は、「外れ値(大きなズレ)」を極端に巨大化させる性質があります。
- ズレが 2 のとき → $2^2 = 4$
- ズレが 10 のとき → $10^2 = 100$
少しでも異常なデータが混じると、カイ二乗値($\chi^2$)は右側にビヨーンと大きく引っ張られます。
その結果、右に長い裾野(すその)を持つ形になるのです。
4. QC検定での注意点:上側と下側
この「左右非対称」という性質は、試験や実務で表を読み取る時にミスを誘発します。
「異常(バラつきすぎ)」を検定したいときは、分布の右端(上側確率)を見ます。
逆に、「精度が良すぎる(データ改ざんの疑い?)」を検定したいときは、左端(下側確率)を見ます。
| 見たいもの | 見るべき場所 | 表の記号(例) | 値のイメージ |
|---|---|---|---|
| バラつきすぎ (異常) |
右端 5% (上側確率) |
$\chi^2_{0.05}$ | 大きい数字 (例: 16.92) |
| バラつかなすぎ (不自然) |
左端 5% (下側確率) |
$\chi^2_{0.95}$ | 0に近い数字 (例: 3.33) |
※表によっては「0.95」が「左側の面積」を指す場合と、「右側の面積」を指す場合がありますが、「大きい数字が右(異常)、小さい数字が左(静寂)」と覚えておけば間違いありません。
まとめ
カイ二乗分布が歪んでいる理由は、「バラつきにはマイナスがなく、プラス方向には青天井だから」でした。
さて、ここまでは「1つの機械」のバラつきを見てきました。
しかし、実務で本当によくあるのは、こんなシチュエーションではないでしょうか?
- 「古い機械Aと、新しい機械B。どっちが優秀(バラつきが小さい)か比べたい!」
- 「工場Aと工場B、品質が安定しているのはどっち?」
2つのバラつきを比較するとき、カイ二乗検定は使えません。
次回は、2つの怪獣(バラつき)を戦わせるためのリング、「F検定」の世界へ進みます。