- アローダイアグラムの図を見ても、どう読めばいいかわからない
- クリティカルパスの求め方がいまいちピンとこない
- 「最早開始時刻」「最遅完了時刻」の違いがごちゃごちゃになる
- QC検定や中小企業診断士の試験で毎回間違えてしまう
- アローダイアグラムの基本的な読み方と記号の意味
- クリティカルパスを確実に見つける方法
- 最早・最遅時刻の計算手順(具体例つき)
- 日程短縮問題の解き方のコツ
「アローダイアグラム」って、図を見た瞬間に「うわ、難しそう…」と感じますよね。
でも安心してください。実は考え方自体はとてもシンプルなんです。
この記事では、アローダイアグラムを「プロジェクトの道順を示した地図」として捉え、初心者でも迷わず解けるように徹底解説します。QC検定2級・3級、中小企業診断士試験でも頻出のテーマなので、ぜひマスターしていきましょう。
目次
アローダイアグラムとは?|プロジェクトの「道順」を見える化したもの
まずは「何のための図なのか」を理解しよう
アローダイアグラム(PERT図とも呼ばれます)は、プロジェクトの作業順序と所要時間を視覚化した図です。
たとえば、新製品を開発するプロジェクトを考えてみましょう。
- 設計が終わらないと、製造は始められない
- 部品Aと部品Bの両方が届かないと、組み立てはできない
- 検査が終わらないと、出荷はできない
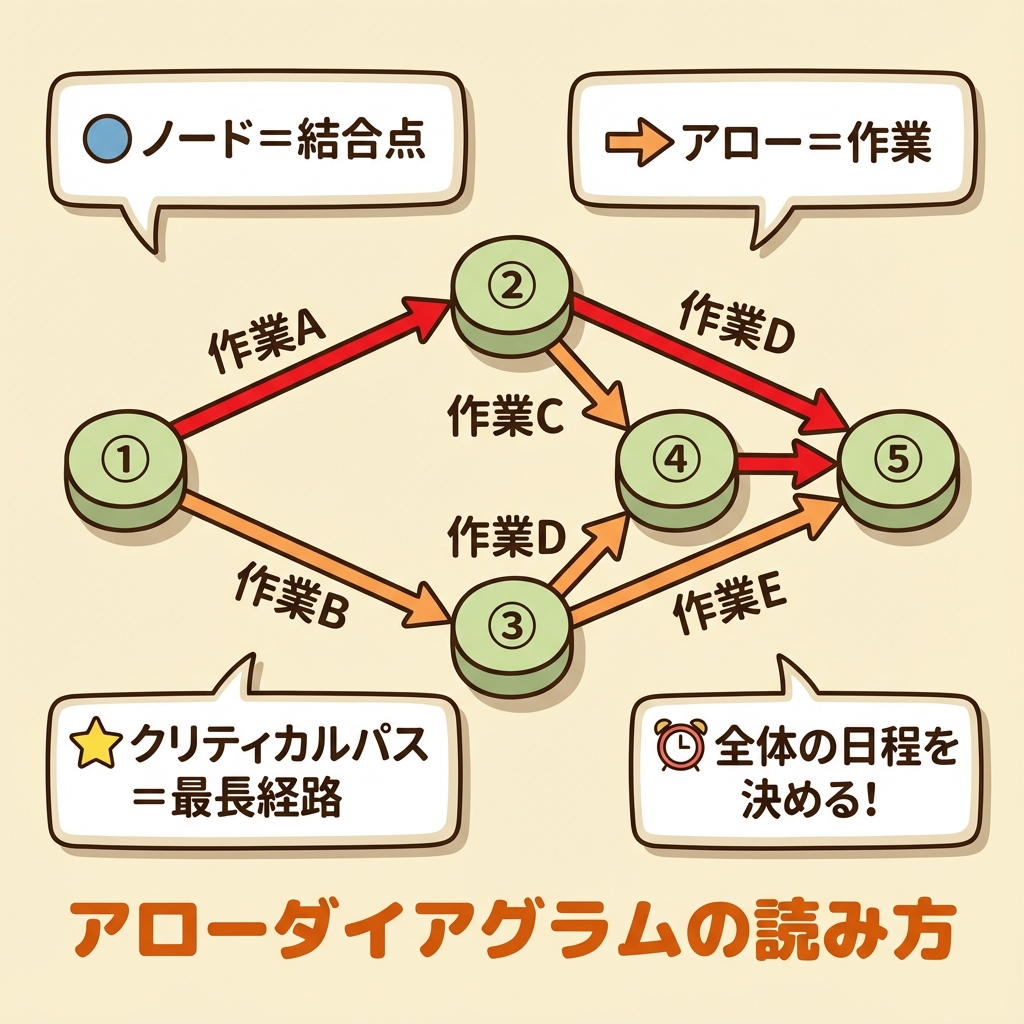
このように、「どの作業が終わらないと次に進めないか」という依存関係を矢印で表現したのがアローダイアグラムです。
アローダイアグラムは「プロジェクトのカーナビ」のようなもの。
スタート地点からゴールまで、どのルートを通ればいいか、どのルートが一番時間がかかるかを教えてくれます。
図の構成要素を覚えよう(たった3つだけ!)
アローダイアグラムに登場する記号は、基本的に3つだけです。
| 記号 | 名前 | 意味 | 例え |
|---|---|---|---|
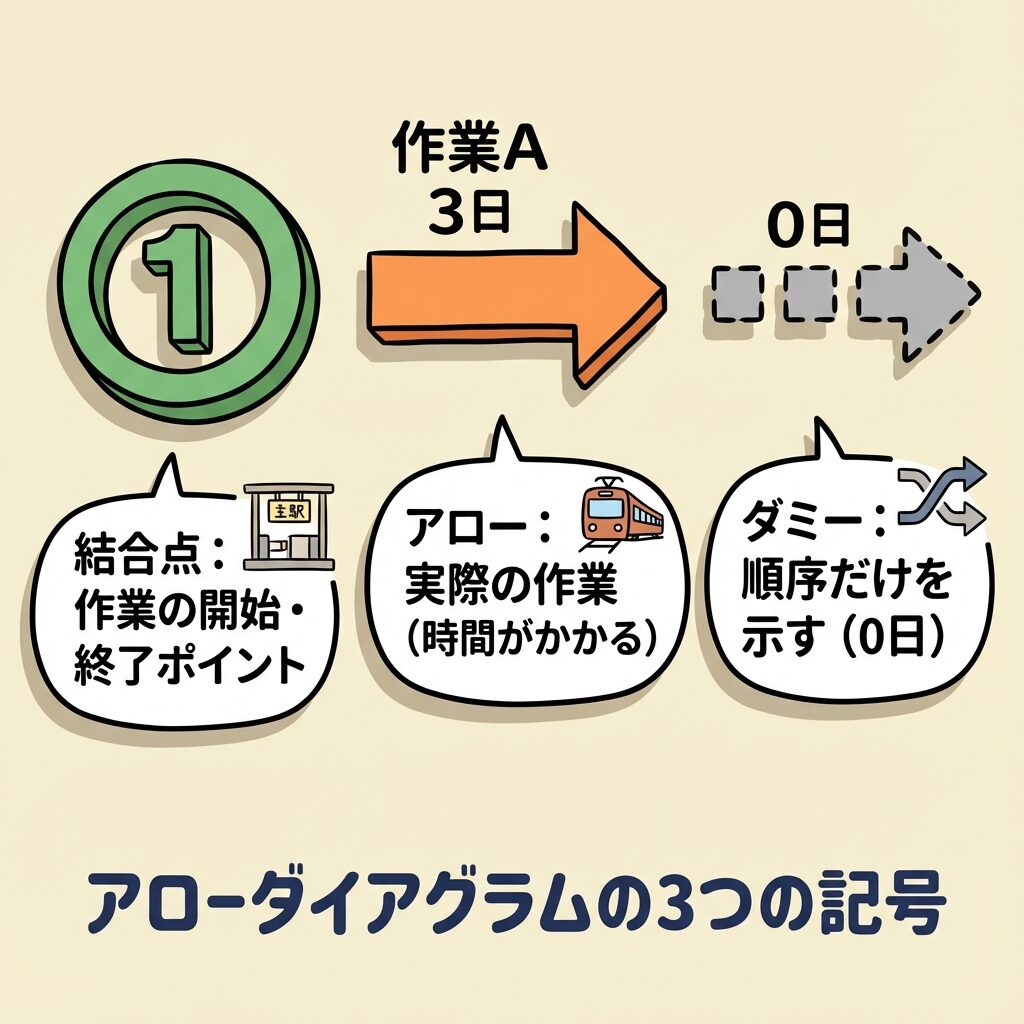
| ○(丸) | ノード(結合点) | 作業の開始点・終了点 | 駅・チェックポイント |
| →(実線矢印) | アロー(作業) | 実際の作業(時間がかかる) | 駅から駅への移動 |
| - - →(点線矢印) | ダミー作業 | 順序関係だけを示す(0日) | 乗り換え(移動時間なし) |
ダミー作業って何?
ダミー作業は、「作業時間は0日だけど、順番の関係を示すために必要な矢印」です。
たとえば、「作業Aと作業Bの両方が終わらないと作業Dを始められない」という関係を表現するために使います。実際には何も作業しないけど、「待っている」という関係を示すわけですね。
ダミー作業の所要日数は必ず0日です。計算時に忘れずに!
クリティカルパスとは?|プロジェクトの「ボトルネック」を見つける
クリティカルパス=「最も時間がかかる経路」
クリティカルパスは、アローダイアグラムの中で最も重要な概念です。
簡単に言うと、「スタートからゴールまでの全ルートの中で、一番時間がかかる経路」のことです。
クリティカルパス = プロジェクト全体の所要日数を決める最長経路
なぜ「最長」が重要なのか?
プロジェクトは、すべての作業が終わらないと完了できません。
たとえば、3つのルートがあって、それぞれ5日、6日、4日かかるとします。一番短い4日のルートが終わっても、6日のルートが終わるまでプロジェクトは完了しませんよね。
だから、「最長経路(=クリティカルパス)の日数」=「プロジェクト全体の最短完了日数」になるのです。
友達5人で待ち合わせをするとき、「全員が揃う時刻」は「一番遅く来る人の到着時刻」で決まりますよね。
クリティカルパスも同じ。「一番時間がかかる経路」がプロジェクト全体の完了時刻を決めるのです。
クリティカルパスの3つの特徴
| 特徴 | 意味 | 実務での意味 |
|---|---|---|
| ①最長経路 | 所要日数の合計が最大 | プロジェクト期間を決める |
| ②余裕ゼロ | 遅延の余裕(フロート)がない | 1日でも遅れると全体が遅れる |
| ③重点管理対象 | 最優先で進捗管理すべき | リソースを集中投入すべき |
【実践】クリティカルパスを求めてみよう
具体的な例で、クリティカルパスの求め方を見ていきましょう。
例題の設定
| 作業 | 所要日数 | 先行作業 |
|---|---|---|
| A | 3日 | なし |
| B | 2日 | なし |
| C | 1日 | A |
| D | 2日 | A, B |
| E | 1日 | C, D |
ステップ1:すべての経路を洗い出す
スタート(①)からゴール(⑤)まで、考えられるすべてのルートを書き出します。
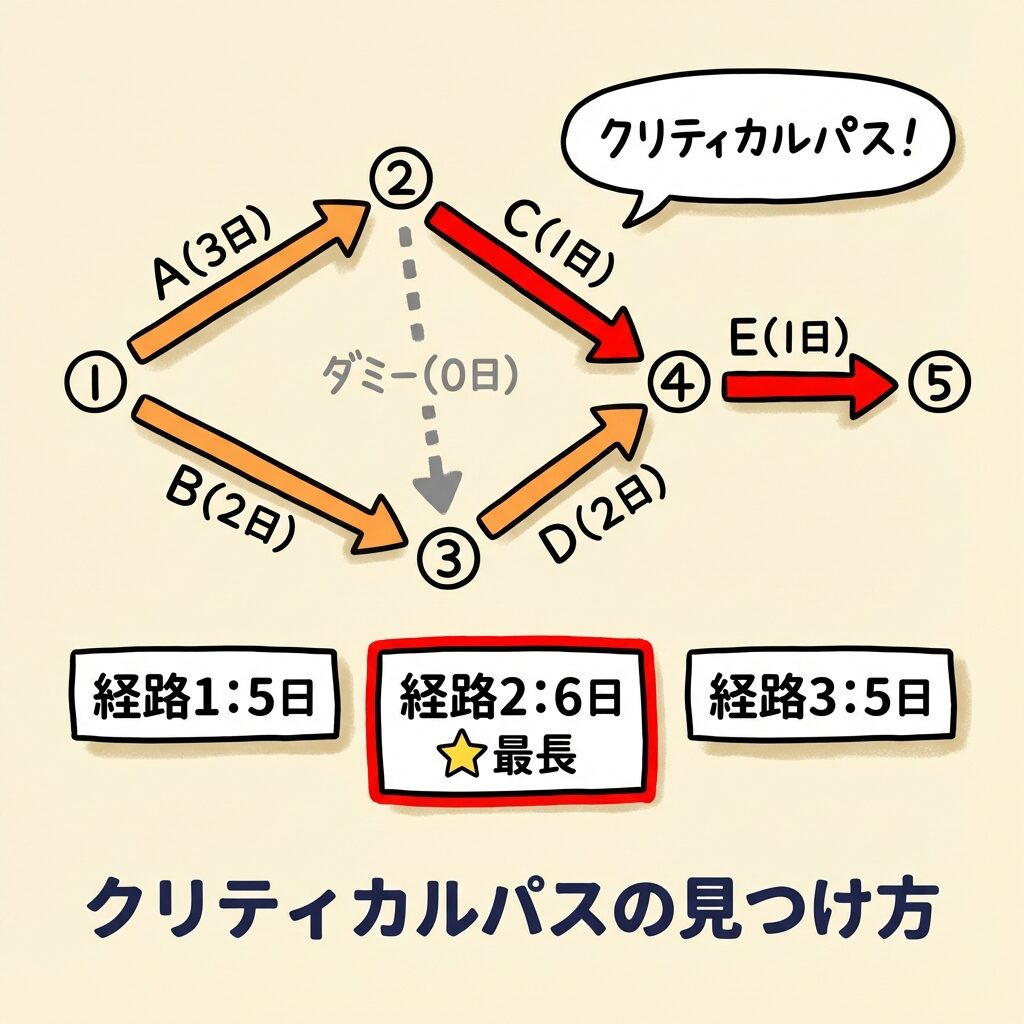
- 経路1:①→②→④→⑤(作業A→C→E)
- 経路2:①→②→③→④→⑤(作業A→ダミー→D→E)
- 経路3:①→③→④→⑤(作業B→D→E)
ステップ2:各経路の所要日数を計算する
| 経路 | 通る作業 | 計算式 | 合計 |
|---|---|---|---|
| 経路1 | A→C→E | 3 + 1 + 1 | 5日 |
| 経路2 | A→ダミー→D→E | 3 + 0 + 2 + 1 | 6日 ←最長! |
| 経路3 | B→D→E | 2 + 2 + 1 | 5日 |
ステップ3:最長経路がクリティカルパス
クリティカルパス:①→②→③→④→⑤(経路2)
プロジェクト全体の最短完了日数:6日
最早開始時刻と最遅完了時刻|「いつ始められる?いつまでに終わればいい?」
アローダイアグラムの問題でよく出てくる「最早開始時刻」と「最遅完了時刻」。名前は難しそうですが、実はとてもシンプルな概念です。
最早開始時刻とは?
その作業を「最も早く」開始できる時刻
=先行作業がすべて終わる最も遅い時刻
たとえば、作業Eを始めるには「作業Cと作業Dの両方が終わっている」必要があります。
作業Cが4日目に終わり、作業Dが5日目に終わるなら、作業Eは5日目(遅い方)からしか始められません。
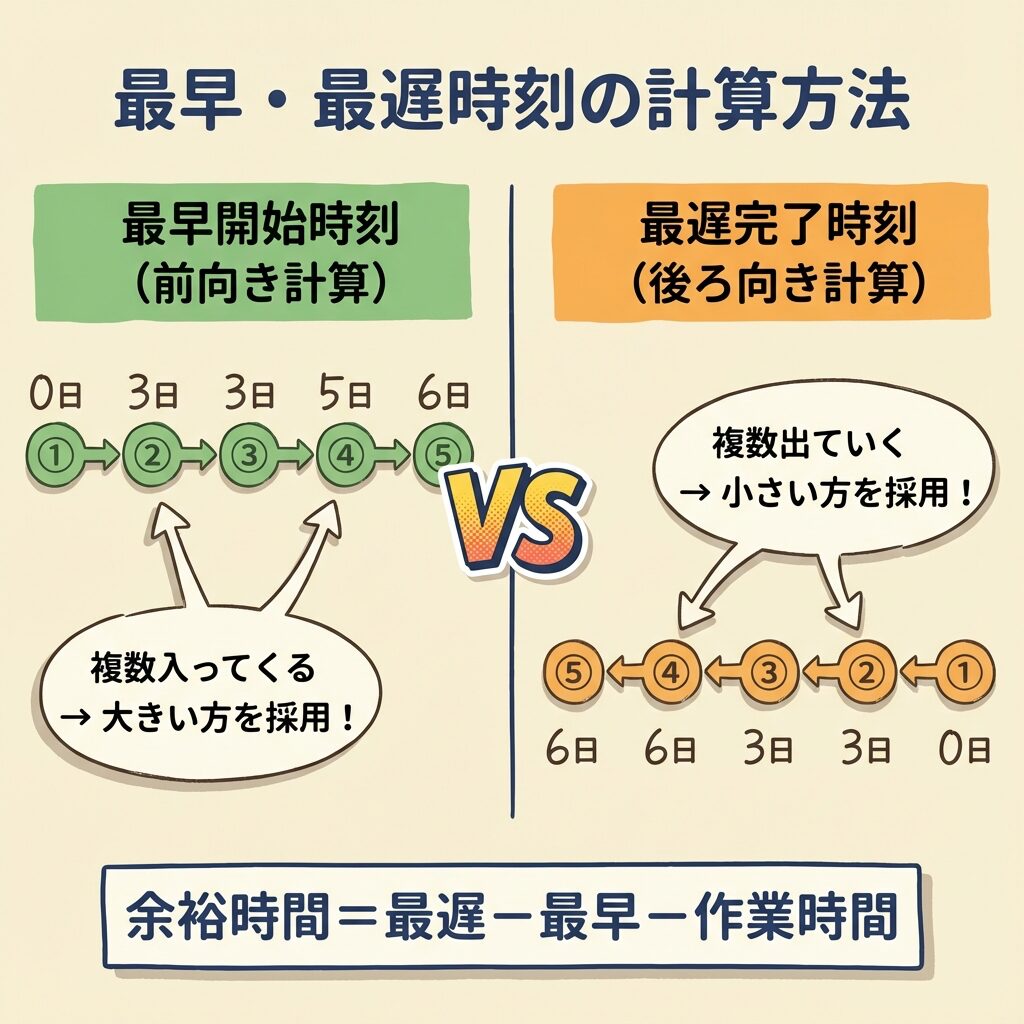
最早開始時刻は「前向き計算」で求める。
スタートから順番に、各ノードに到達できる最も早い時刻を計算していく。
複数の矢印が入ってくるノードでは「大きい方」を採用!
【実践】最早開始時刻を計算してみよう
先ほどの例題で、各ノードの最早開始時刻を計算します。
| ノード | 計算 | 最早時刻 |
|---|---|---|
| ①(スタート) | 基準 | 0日目 |
| ② | 0 + 3(作業A) | 3日目 |
| ③ | max(0+2, 3+0) = max(2, 3) | 3日目 |
| ④ | max(3+1, 3+2) = max(4, 5) | 5日目 |
| ⑤(ゴール) | 5 + 1(作業E) | 6日目 |
最遅完了時刻とは?
その作業を「遅くともこの時刻までに」終わらせないと全体が遅れる時刻
=後続作業に間に合うギリギリの時刻
最遅完了時刻は、「これ以上遅れたらプロジェクト全体に影響が出る」というデッドラインのようなものです。
最遅完了時刻は「後ろ向き計算」で求める。
ゴールから逆算して、各ノードに到達していないといけない最も遅い時刻を計算。
複数の矢印が出ていくノードでは「小さい方」を採用!
余裕時間(フロート)とは?
最早開始時刻と最遅完了時刻の差が「余裕時間(フロート)」です。
余裕時間が0の作業はクリティカルパス上にあるということ。遅れたら即、プロジェクト全体に影響します。
「作業○の余裕時間を求めよ」という問題がよく出ます。
最早・最遅時刻を正確に計算できれば、簡単に解けます!
日程短縮のコツ|どの作業を短くすれば効果的?
プロジェクトの納期を早めたいとき、「どの作業を短縮すればいいか?」という問題がよく出題されます。
ここで重要なのが、「クリティカルパス上の作業だけが全体に影響する」という原則です。
日程短縮の鉄則
① クリティカルパス上の作業を短縮しないと、全体は短くならない
② クリティカルパス以外の作業をいくら短縮しても効果なし
③ 短縮すると、別の経路がクリティカルパスになることがある
なぜクリティカルパス以外を短縮しても無駄なのか?
先ほどの例で考えてみましょう。
クリティカルパスは経路2(6日)で、経路1と経路3は5日でした。
ここで経路3の作業B(2日→1日)を短縮したらどうなるでしょう?
- 経路3:2 + 2 + 1 → 1 + 2 + 1 = 4日に短縮
- でも、経路2(クリティカルパス)は6日のまま
- 結果:プロジェクト全体は6日のまま変わらない!
これが「クリティカルパス以外を短縮しても無駄」という意味です。
【実践】日程短縮問題を解いてみよう
先ほどの例題に「短縮コスト」が追加された問題を考えます。
| 作業 | 所要日数 | 半分にするコスト | 短縮できる日数 |
|---|---|---|---|
| A ⭐ | 3日 | 2 | 1.5日 |
| B | 2日 | 2 | 1日 |
| C | 1日 | 2 | 0.5日 |
| D ⭐ | 2日 | 3 | 1日 |
| E ⭐ | 1日 | 1 | 0.5日 |
⭐マークがクリティカルパス上の作業(A→ダミー→D→E)です。
問題:コスト3で最大何日短縮できる?
ステップ1:クリティカルパス上の作業だけに注目する
ステップ2:コスト効率の良い組み合わせを探す
- 作業A短縮(コスト2)+ 作業E短縮(コスト1)= コスト3
- 短縮日数:1.5日 + 0.5日 = 2日?
ステップ3:短縮後にクリティカルパスが変わらないか確認!
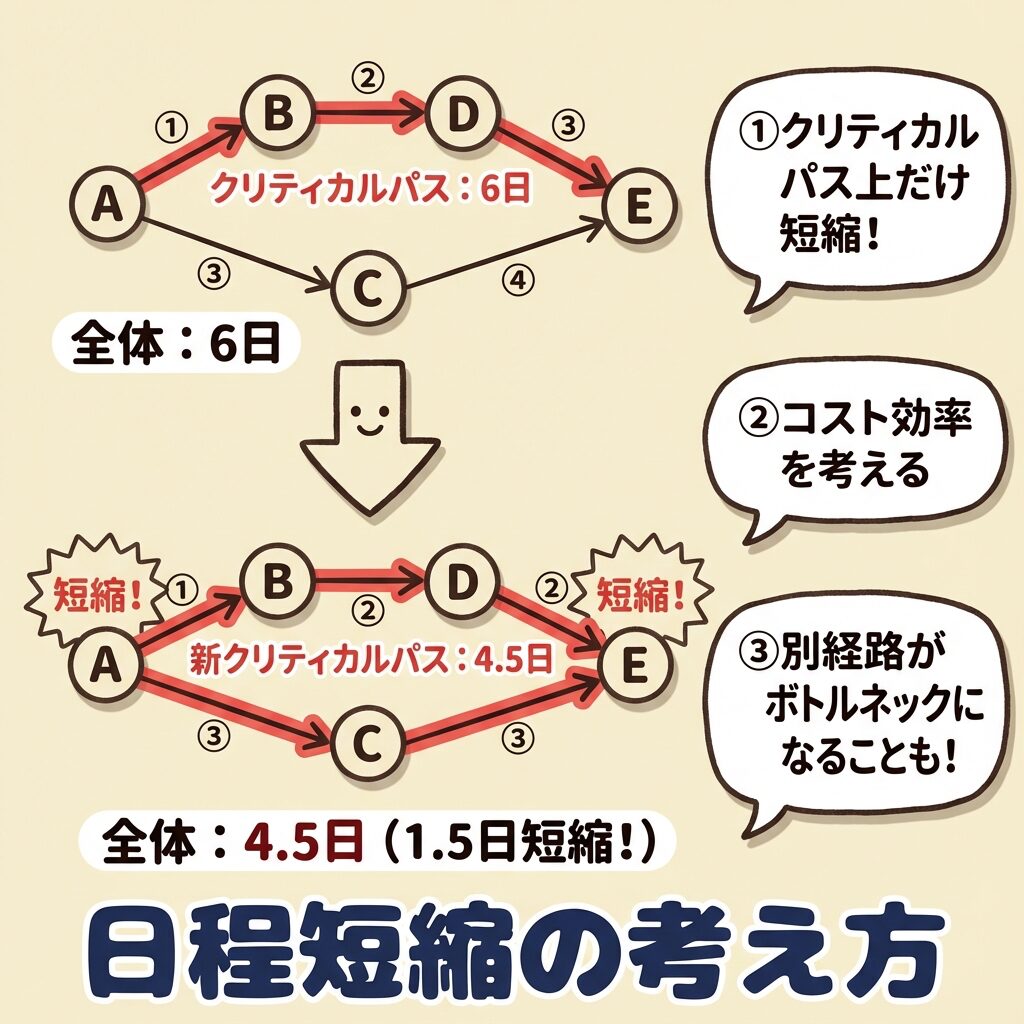
作業Aを1.5日短縮すると:
- 経路2(元クリティカルパス):1.5 + 0 + 2 + 0.5 = 4日
- 経路3(B→D→E):2 + 2 + 0.5 = 4.5日 ← こっちが新たなボトルネックに!
経路3がクリティカルパスになるため、全体は4.5日までしか短縮できません。
元の6日 → 4.5日 = 1.5日短縮が最大
「クリティカルパス上の作業を短縮した日数」=「全体の短縮日数」とは限りません!
必ず、短縮後に他の経路がクリティカルパスになっていないか確認しましょう。
まとめ|アローダイアグラム攻略のポイント
この記事で解説したアローダイアグラムのポイントを整理します。
① アローダイアグラムの基本
・ノード(丸)=結合点、アロー(矢印)=作業、ダミー(点線)=順序関係のみ
② クリティカルパス
・最長経路がプロジェクト全体の日数を決める
・この経路上の作業は余裕ゼロ(遅れたら即アウト)
③ 最早・最遅時刻
・最早開始時刻:前向き計算、複数入ってくるなら「大きい方」
・最遅完了時刻:後ろ向き計算、複数出ていくなら「小さい方」
④ 日程短縮
・クリティカルパス上の作業だけを短縮する
・短縮後に別経路がクリティカルパスになることに注意
試験対策のワンポイントアドバイス
アローダイアグラムの問題は、一見複雑に見えますが、手順を守れば確実に解けます。
- まずは図に数字を書き込む:各ノードの最早時刻を計算しながら記入
- すべての経路を洗い出す:見落としがないように、スタートからゴールまで順番に
- クリティカルパスを特定してから問題を解く:これが基本中の基本
QC検定でも中小企業診断士試験でも、この基本を押さえれば怖くありません。ぜひ何度も練習して、確実に得点源にしてくださいね。
📚 次に読むべき記事
QC検定の実験計画法を体系的に学びたい方におすすめ
統計学の基礎を固めたい方はこちらから
直交表を使った効率的な実験計画を学びたい方へ