- バスタブカーブって何?なぜ「バスタブ(浴槽)」なの?
- 初期故障・偶発故障・摩耗故障の違いがわからない
- DFR・CFR・IFRって何の略?覚えられない…
- 故障率曲線を理解して、実務にどう活かせばいいの?
- バスタブカーブを「人間の一生」でイメージ理解
- 3つの故障期間(初期・偶発・摩耗)の特徴と原因
- DFR・CFR・IFRの意味を「故障率の動き」で覚える
- 各期間に対する適切な対策
製品には「寿命」があります。
でも、その寿命は単純に「○○年で壊れる」というものではありません。製品は、時期によって壊れやすさが変わるんです。
この「時期による壊れやすさの変化」をグラフにしたものが、故障率曲線(バスタブカーブ)です。
なぜ「バスタブ(浴槽)」かというと、グラフの形がお風呂の浴槽を横から見た形に似ているからです。
この記事では、バスタブカーブを「人間の一生」に例えて、直感的に理解できるように解説します。
目次
バスタブカーブを「人間の一生」で理解する
製品の一生は、実は人間の一生とよく似ています。
この例え話を理解すれば、バスタブカーブは一発で覚えられます。
製品の一生 = 人間の一生
| 製品の時期 | 人間に例えると | 特徴 |
|---|---|---|
| 初期故障期間 | 👶 赤ちゃん〜幼児期 | 生まれたばかりで不安定。病気になりやすい |
| 偶発故障期間 | 👨 成人期(働き盛り) | 体力があり安定。病気は少ないが、事故は起きうる |
| 摩耗故障期間 | 👴 老年期 | 体が衰えてくる。病気が増える |
このように考えると、バスタブカーブの形が自然に理解できますよね。
- 赤ちゃん:まだ体が弱く、病気になりやすい → 故障率が高い
- 成人:体力があり、めったに病気にならない → 故障率が低い
- 老人:体が衰え、病気が増える → 故障率が高くなる
製品も人間も、「最初」と「最後」に問題が起きやすく、「真ん中」が一番安定しているという点で同じです。
だからグラフが「浴槽」の形(両端が高く、真ん中が低い)になるんです。
① 初期故障期間(DFR:故障率が減少する時期)
初期故障期間とは?
製品を使い始めた直後の期間です。故障率が高いところから、だんだん下がっていきます。
Decreasing = 減少する
故障率が時間とともに下がっていく期間
なぜ最初は故障率が高いのか?
製品が生まれたばかりのとき、こんな問題が隠れている可能性があります。
| 原因の種類 | 具体例 |
|---|---|
| 設計ミス | 強度不足、放熱設計の不備、部品選定ミス |
| 製造ミス | はんだ不良、組立ミス、異物混入 |
| 材料不良 | 不良部品の混入、材料のバラつき |
これらの「生まれつきの問題」を持った製品は、使い始めてすぐに壊れます。
逆に言うと、問題のある製品が早めに脱落していくので、残った製品の故障率は下がっていきます。
イメージ:学校のマラソン大会
スタート直後は、体調不良の人がどんどん脱落する
↓
残った人は体力があるので、しばらく安定して走れる
初期故障期間への対策
初期故障を「お客様に届く前に」取り除くことが重要です。
| 対策 | 内容 |
|---|---|
| バーンイン試験 | 出荷前に高温などの厳しい条件で動かし、初期不良をあえて発生させて取り除く |
| エージング | 一定時間動かしてから出荷する(慣らし運転) |
| 出荷検査 | 全数または抜取りで検査し、不良品を除去 |
| デバッグ | ソフトウェアのバグを出荷前に修正 |
「お客様の手元で壊れる前に、工場で壊してしまおう」という考え方です。
高温で100時間動かして壊れなかった製品だけを出荷すれば、お客様の元では初期故障が起きにくくなります。

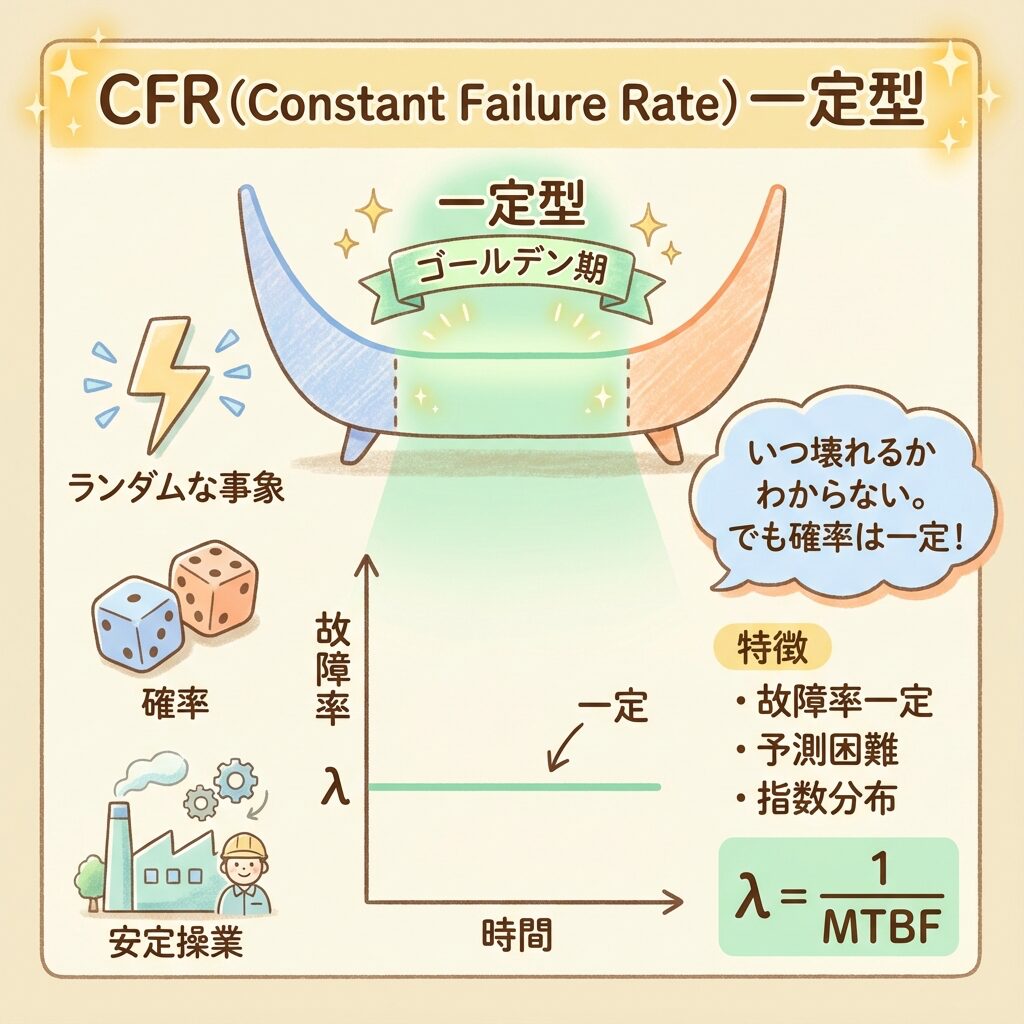
② 偶発故障期間(CFR:故障率が一定の時期)
偶発故障期間とは?
初期故障期間を過ぎ、摩耗故障期間に入るまでの安定した期間です。
この期間は故障率が一定(低いまま変わらない)で、製品が最も安定して動く「黄金期」です。
Constant = 一定の
故障率が時間によらず一定の期間
偶発故障の特徴:「いつ壊れるかわからない」
偶発故障期間の故障は、予測できません。
「昨日まで元気だったのに、突然壊れた」というのが偶発故障です。
イメージ:サイコロを振る
毎回「1が出たら故障」というゲーム
↓
いつ1が出るかは完全にランダム
↓
でも「1が出る確率」は毎回同じ(1/6)
これが「故障率が一定」の意味です。
偶発故障の原因
偶発故障は、製品自体の問題ではなく、外部からのランダムな要因で起こります。
| 原因 | 例 |
|---|---|
| 環境ストレス | 落雷、過電圧、温度変化、振動 |
| 使用ミス | 落下、水没、誤操作 |
| 偶発的な部品故障 | 突然のコンデンサ破裂、接触不良 |
故障率一定 = 指数分布
偶発故障期間では、故障間隔は「指数分布」に従うことが知られています。
このとき、故障率λとMTBFには次の関係があります。
λ = 1 / MTBF
故障率と平均故障間隔は逆数の関係(故障率一定のときだけ成り立つ)
λ = 1/MTBF の関係は、偶発故障期間(故障率一定)のときだけ成り立ちます。
初期故障期間や摩耗故障期間では、故障率が変化するので、この単純な関係は使えません。
偶発故障期間への対策
偶発故障は予測できないので、「起きても大丈夫」な設計にすることが重要です。
| 対策 | 内容 |
|---|---|
| 冗長設計 | 重要な部品を二重化して、1つ壊れても動くようにする |
| フェイルセーフ設計 | 壊れたときに安全な状態になるよう設計する |
| 監視・アラート | 故障をすぐに検知して対応できるようにする |
③ 摩耗故障期間(IFR:故障率が増加する時期)
摩耗故障期間とは?
製品を長く使い続けると、やがて部品が劣化して故障率が上がってくる時期が来ます。
これが摩耗故障期間です。人間で言えば「老年期」にあたります。
Increasing = 増加する
故障率が時間とともに上がっていく期間
摩耗故障の原因
摩耗故障は、時間の経過とともに蓄積するダメージが原因です。
| 原因 | 例 |
|---|---|
| 機械的摩耗 | ベアリングの摩耗、ブレーキパッドの減り |
| 金属疲労 | 繰り返し応力による亀裂、破断 |
| 腐食・酸化 | 錆び、配線の腐食 |
| 経年劣化 | ゴムの硬化、プラスチックの脆化、電解コンデンサのドライアップ |
摩耗故障の特徴:「予測できる」
偶発故障とは違い、摩耗故障はある程度予測できます。
なぜなら、劣化は時間とともに進むので、「そろそろ寿命」という予兆があるからです。
イメージ:車のタイヤ
走るほど溝が減っていく
↓
「あと○○km走ったら交換」と予測できる
↓
壊れる前に交換すれば問題なし
摩耗故障期間への対策
摩耗故障は予測できるので、壊れる前に手を打つ「予防保全」が有効です。
| 対策 | 内容 |
|---|---|
| 予防保全 | 壊れる前に定期的に部品を交換する |
| 状態監視保全 | 振動、温度などを監視し、異常を検知したら交換 |
| 寿命管理 | 使用時間や回数を記録し、寿命が来たら交換 |
| 設計による対策 | 長寿命部品の採用、交換しやすい設計 |
「壊れてから直す」のではなく、「壊れる前に交換する」という考え方です。
車のエンジンオイル交換が良い例です。オイルが劣化してエンジンが壊れる前に、定期的に交換しますよね。

DFR・CFR・IFRの覚え方
3つの略語は、故障率の「動き」を表しています。
| 略語 | 英語 | 意味 | 故障率の動き |
|---|---|---|---|
| DFR | Decreasing FR | 減少型 | ↘️ 下がる |
| CFR | Constant FR | 一定型 | ➡️ 横ばい |
| IFR | Increasing FR | 増加型 | ↗️ 上がる |
「D(ダウン)→ C(コンスタント)→ I(インクリース)」
下がる → 一定 → 上がる の順番で覚える
まとめ:バスタブカーブの全体像
この記事で学んだことを整理しましょう。
✅ バスタブカーブの3つの期間
| 期間 | 故障率 | 原因 | 対策 |
|---|---|---|---|
| 初期故障 (DFR) |
減少 ↘️ | 設計ミス、製造不良 | バーンイン、出荷検査 |
| 偶発故障 (CFR) |
一定 ➡️ | ランダム事象 | 冗長設計、監視 |
| 摩耗故障 (IFR) |
増加 ↗️ | 摩耗、劣化、疲労 | 予防保全、部品交換 |
✅ 人間の一生との対応
👶 赤ちゃん(初期故障)→ 👨 成人(偶発故障)→ 👴 老人(摩耗故障)
✅ 重要な関係式
λ = 1 / MTBF(偶発故障期間のみ成立)
- バスタブカーブの形:両端が高く、真ん中が低い「浴槽型」
- DFR:Decreasing(減少)、初期故障期間
- CFR:Constant(一定)、偶発故障期間、指数分布
- IFR:Increasing(増加)、摩耗故障期間
- λ = 1/MTBF:CFR(故障率一定)のときだけ成立
- バーンイン:初期故障を出荷前に取り除く
- 予防保全:摩耗故障を壊れる前に対策
📚 次に読むべき記事
バスタブカーブの3期間を数学的に表現するワイブル分布を学ぶ
MTBFとMTTRを統合した指標で、システム全体の稼働率を評価
偶発故障への対策「冗長設計」の考え方と計算方法
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


