💭 こんな疑問、ありませんか?
- 「複数の部品を組み合わせたとき、全体の信頼度ってどう計算するの?」
- 「直列と並列で、なぜ計算式が違うの?」
- 「冗長設計って、具体的にどういう仕組み?」
✅ この記事でわかること
- 信頼性ブロック図(RBD)とは何か、なぜ必要か
- 直列系の信頼度=「掛け算」で下がる理由
- 並列系の信頼度=「1から引いて掛けて1から引く」で上がる理由
- 冗長系の考え方と種類(待機冗長・並列冗長)
- 複合系の計算方法=分解して順番に解くテクニック
📌 結論(3秒で理解)
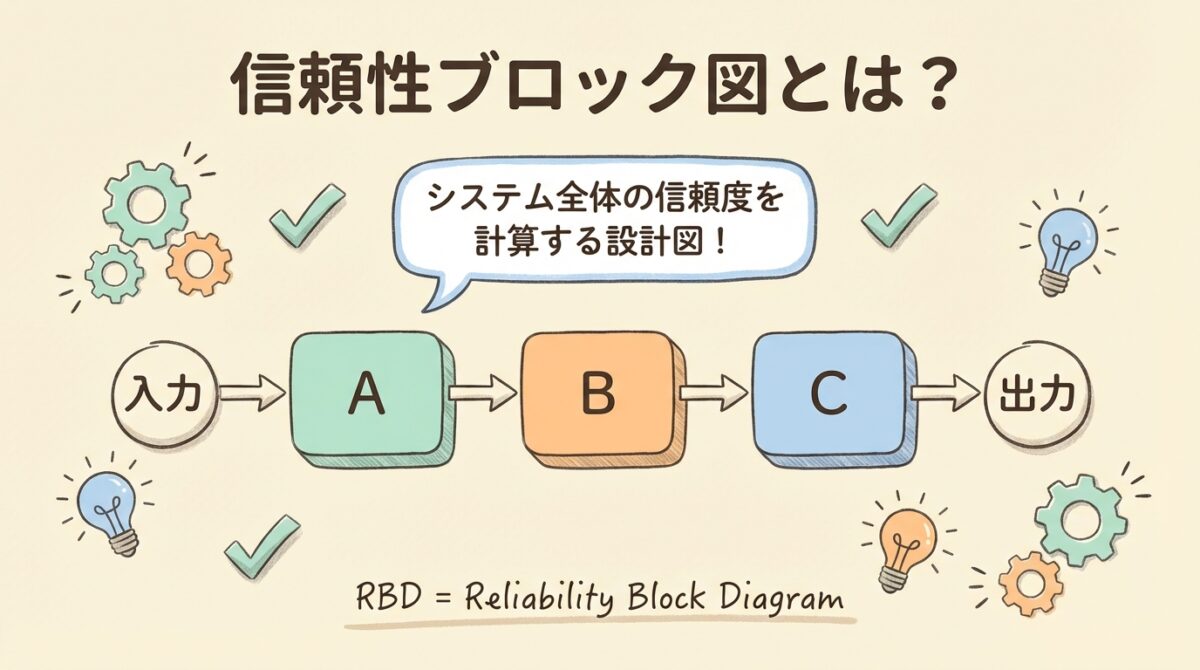
信頼性ブロック図とは、システムを構成する部品の「つながり方」を図にして、全体の信頼度を計算する設計図です。
直列なら「掛け算」、並列なら「補い合い」で計算します。
スマートフォン、自動車、飛行機、工場のライン。
私たちの身の回りには、たくさんの部品が組み合わさったシステムがあります。
ここで、ふと疑問が浮かびます。
「部品が10個あって、それぞれ99%の信頼度なら、全体は何%?」
答えは「つながり方」によって変わります。
直列(1つでも壊れたらアウト)なのか、並列(どれか1つ動けばOK)なのかで、全然違う結果になるのです。
この「つながり方」を図にして、全体の信頼度を計算するのが信頼性ブロック図(RBD:Reliability Block Diagram)です。
目次
🎯 信頼性ブロック図(RBD)とは?
📖 信頼性ブロック図の定義
システムを構成する各部品(ユニット)の「信頼性上のつながり方」を図にしたもの。
この図を使って、システム全体の信頼度を計算します。
別名:RBD(Reliability Block Diagram)
💡 なぜブロック図が必要なのか?
たとえば、こんな状況を考えてみてください。
🏭 工場のラインを設計中…
「この機械、信頼度90%の部品を3つ使ってるけど、全体では何%の信頼度になるの?」
答えは…「つなぎ方」によって全然違います!
この「つなぎ方」を明確にして計算するのが、信頼性ブロック図の役割です。
主に3つのパターンがあります。
① 直列系
1つでも壊れたらアウト
② 並列系
全部壊れなければOK
③ 冗長系
予備を持っておく
🔴 直列系 ─「1つでも壊れたらアウト」
📖 直列系とは
すべての部品が正常に動いて初めて、システム全体が動く構成。
1つでも故障したら、全体が停止する。
🎄 クリスマスツリーの電飾で理解する
直列系の身近な例は、昔のクリスマスツリーの電飾です。
💡 直列接続の電球
昔の電飾は、電球が1本の線で数珠つなぎになっていました。
もし1個の電球が切れると…
→ 電気の流れが止まる → 全部の電球が消える!
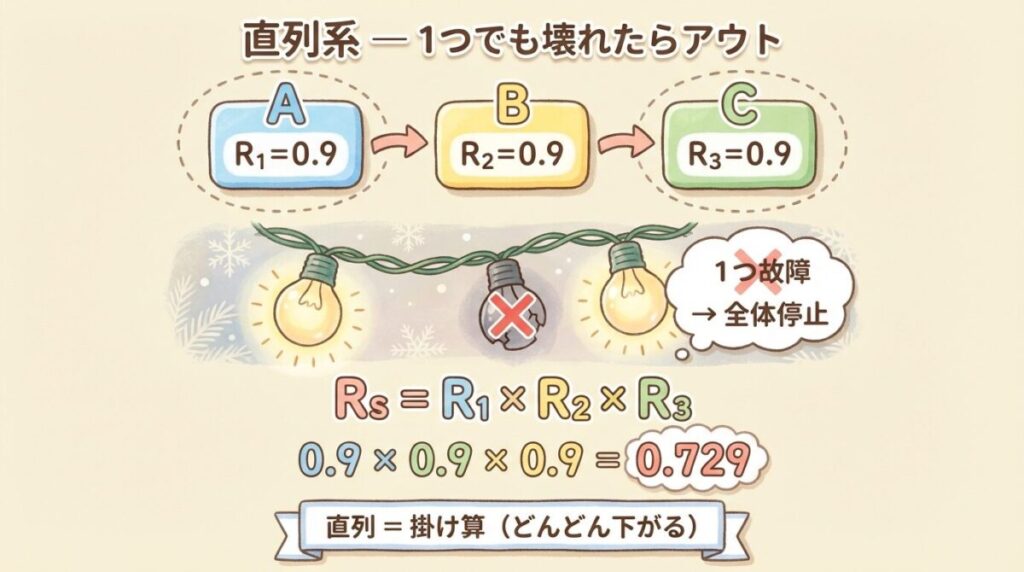
これが「直列系」のイメージです。
📐 直列系の公式
🔑 直列系の信頼度公式
Rs = R₁ × R₂ × R₃ × … × Rn
各部品の信頼度を「掛け算」する
🤔 なぜ「掛け算」なのか?
直列系が動くには、すべての部品が同時に正常でなければなりません。
確率の世界では、「AかつBかつC」が起きる確率は、それぞれの確率を掛け算します。
P(AかつBかつC) = P(A) × P(B) × P(C)
✏️ 計算例:直列系
📝 例題
3つの部品A、B、Cが直列に接続されている。
各部品の信頼度は、それぞれ R₁ = 0.9、R₂ = 0.9、R₃ = 0.9。
システム全体の信頼度は?
📊 計算プロセス
Step 1:公式に数値を代入
Rs = 0.9 × 0.9 × 0.9
Step 2:掛け算して完了!
Rs = 0.729(= 72.9%)
✅ 答え:Rs = 0.729(72.9%)
各部品90%でも、3つ直列にすると約73%に下がる!
⚠️ 直列系の落とし穴
直列系では、部品を増やすほど信頼度が下がります。
例:信頼度90%の部品を10個直列 → 0.910 = 0.349(約35%)
だから、重要なシステムでは「並列」や「冗長」を使うのです。
🟢 並列系 ─「全部壊れなければOK」
📖 並列系とは
複数の部品のうち、1つでも正常に動いていれば、システム全体が動く構成。
全部が故障したときだけ、全体が停止する。
🚇 駅のエスカレーターで理解する
並列系の身近な例は、駅のエスカレーターです。
💡 3台並んだエスカレーター
大きな駅では、エスカレーターが3台並んでいることがあります。
もし1台が故障しても…
→ 残り2台が動いている → 乗客は問題なく移動できる!
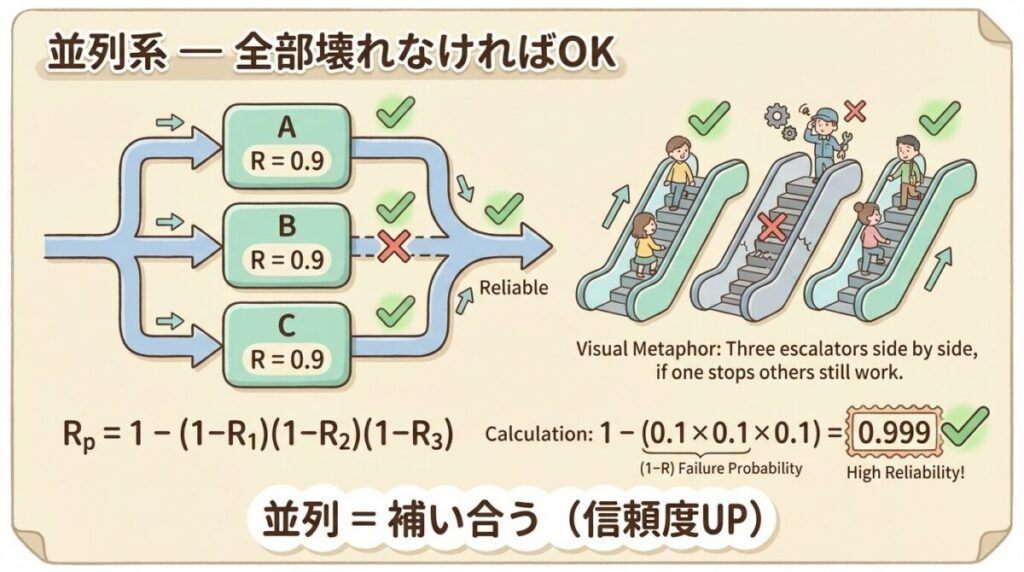
全部が同時に故障しない限り、機能は維持されます。これが「並列系」のイメージです。
📐 並列系の公式
🔑 並列系の信頼度公式
Rp = 1 − (1−R₁)(1−R₂)(1−R₃)…(1−Rn)
「1から引いて掛けて、1から引く」
🤔 なぜこの式になるのか?
並列系が故障するのは、「すべての部品が同時に故障」したとき。
① 各部品の「故障確率」を求める
故障確率 = 1 − 信頼度 例:R = 0.9 なら、故障確率 = 0.1
② 「全部が故障」の確率を求める
全部故障 = 0.1 × 0.1 × 0.1 = 0.001
③ 「1つでも動く」確率を求める
システム信頼度 = 1 − 0.001 = 0.999
これを1つの式にまとめたのが、並列系の公式です。
✏️ 計算例:並列系
📝 例題
3つの部品A、B、Cが並列に接続されている。
各部品の信頼度は、それぞれ R₁ = 0.9、R₂ = 0.9、R₃ = 0.9。
システム全体の信頼度は?
📊 計算プロセス
Step 1:各部品の故障確率を求める
1 − 0.9 = 0.1(各部品とも)
Step 2:「全部故障」の確率を求める
0.1 × 0.1 × 0.1 = 0.001
Step 3:1から引いて完了!
Rp = 1 − 0.001 = 0.999(= 99.9%)
✅ 答え:Rp = 0.999(99.9%)
各部品90%でも、3つ並列にすると99.9%に上がる!
💡 直列 vs 並列の比較(同じ部品3つの場合)
| 接続方式 | 計算式 | 結果 |
|---|---|---|
| 直列系 | 0.9 × 0.9 × 0.9 | 72.9% |
| 並列系 | 1 − (0.1)³ | 99.9% |
同じ部品3つでも、つなぎ方で27%も差が出るのです!
🔵 冗長系 ─「予備を持っておく設計」
📖 冗長系とは
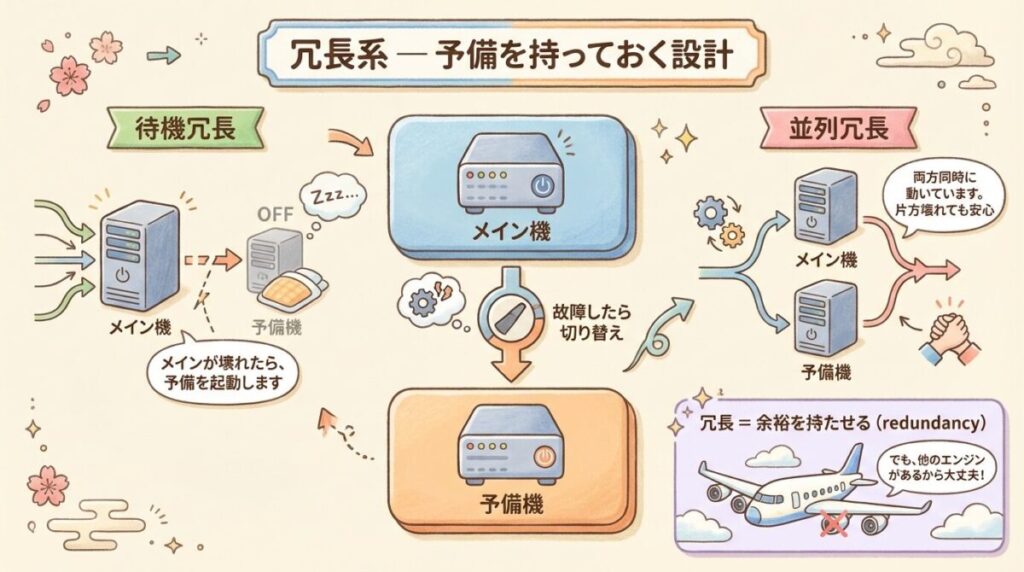
予備の部品やシステムを用意しておき、メインが故障したら切り替える構成。
「冗長」= 余裕・余分(redundancy)を持たせること
✈️ 飛行機のエンジンで理解する
💡 なぜ飛行機のエンジンは複数あるのか?
旅客機には、通常2〜4つのエンジンが搭載されています。
これは「速く飛ぶため」だけでなく、「1つ止まっても飛び続けられる」ため。
実際、双発機はエンジン1つでも着陸できる設計になっています。
これが「冗長設計」の考え方です。
📝 冗長系の2つの種類
① 待機冗長(スタンバイ)
普段は予備機が停止している。
メインが故障したら、予備機を起動して切り替え。
例:データセンターの予備サーバー
✅ メリット:予備機の劣化が少ない
⚠️ デメリット:切り替え時間がかかる
② 並列冗長(アクティブ)
常に複数が同時稼働している。
1つが故障しても、残りがそのまま継続。
例:飛行機のエンジン、RAID
✅ メリット:切り替え不要で瞬断なし
⚠️ デメリット:全機が常に劣化
💡 並列冗長の計算は、並列系と同じ
「常に同時稼働」の並列冗長は、先ほどの並列系の公式で計算できます。
待機冗長は、切り替え成功率などを考慮した別の計算が必要です(発展的内容)。
🟠 複合系の計算 ─「分解して攻略」
現実のシステムは、直列と並列が組み合わさった「複合系」であることがほとんどです。
複雑に見えますが、分解して順番に計算すれば解けます。
📐 複合系の解き方(3ステップ)
-
直列部分を見つけて、まとめて1ブロックにする
直列部分 → 掛け算で1つの信頼度に -
並列部分を見つけて、まとめて1ブロックにする
並列部分 → 「1から引いて掛けて1から引く」で1つに - 簡略化を繰り返して、最終的に1つの値にする
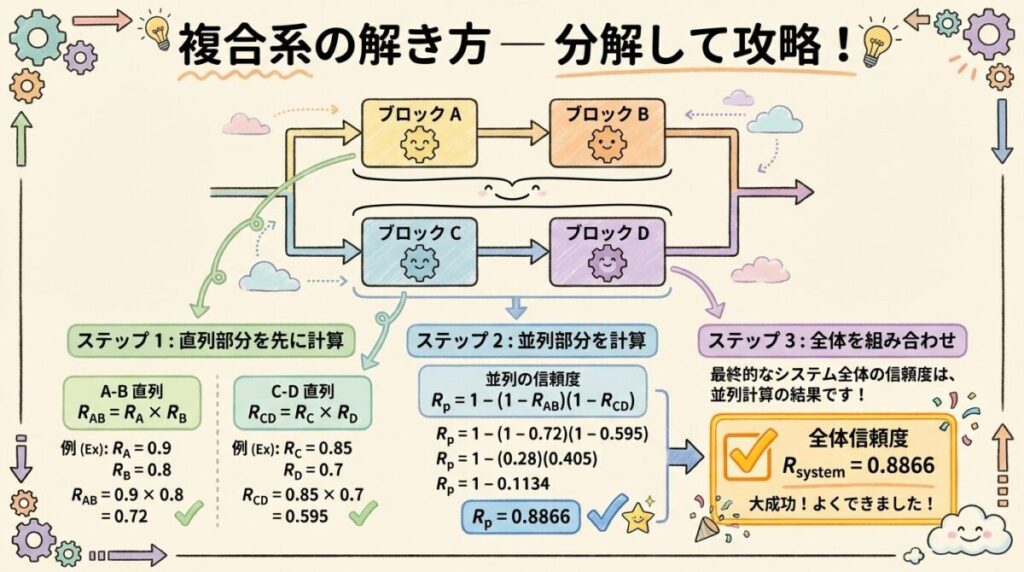
✏️ 計算例:複合系
📝 例題
以下のシステムの信頼度を求めなさい。
│ │
入力 ─┤ ├─ 出力
│ │
└─ C (R=0.9) ─ D (R=0.9) ─┘
上段(A→B直列)と下段(C→D直列)が、並列に接続されている。
📊 計算プロセス
Step 1:直列部分を計算(上段)
R上 = 0.9 × 0.9 = 0.81
Step 2:直列部分を計算(下段)
R下 = 0.9 × 0.9 = 0.81
Step 3:並列部分を計算(上段と下段を合成)
R全体 = 1 − (1 − 0.81)(1 − 0.81) = 1 − (0.19 × 0.19) = 1 − 0.0361
Step 4:完了!
R全体 = 0.9639(= 96.39%)
✅ 答え:R全体 = 0.9639(96.39%)
直列だけなら81%に下がるが、並列にすることで96%以上に回復!
📌 複合系を解くコツ
- 内側から外側へ:一番深い入れ子から計算
- 直列を先に:直列部分を1つにまとめてから並列計算
- 図を描く:複雑な場合は、計算後の図を描いて確認
📝 まとめ
✅ この記事のポイント
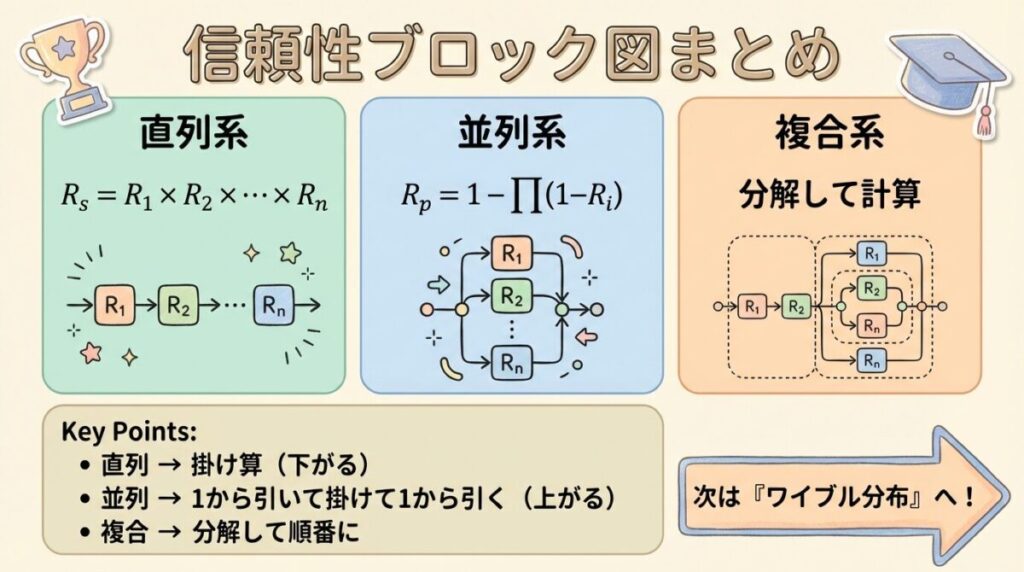
- 信頼性ブロック図(RBD)は、システムの「信頼性上のつながり方」を図にしたもの
-
直列系:1つでも故障 → 全体停止
公式:Rs = R₁ × R₂ × … × Rn(掛け算で下がる) -
並列系:全部故障して初めて停止
公式:Rp = 1 − (1−R₁)(1−R₂)…(補い合いで上がる) -
冗長系:予備を持たせて信頼度を高める設計
待機冗長(スタンバイ)と並列冗長(アクティブ)がある - 複合系:直列部分→並列部分の順に分解して計算
🔑 覚えておくべき公式
直列系
Rs = ∏Ri
並列系
Rp = 1 − ∏(1−Ri)
💡 語呂合わせで覚える
直列=「掛け算」=どんどん下がる
並列=「1から引いて掛けて1から引く」=補い合って上がる
🚀 次に読むべき記事
信頼性ブロック図を理解できたら、次は「故障データの解析」を学びましょう。
実際の故障データから信頼度を推定する方法が、信頼性工学の次のステップです。
📖 NEXT STEP
【実務向け】信頼性データの取り方|打ち切りデータ(中途・定時・定数)の扱い方
寿命試験で得られる「打ち切りデータ」の種類と扱い方を図解。実務での信頼性データ収集の基礎をマスターします。
📚 関連記事
【超入門】信頼性工学とは?|製品が"壊れない"を数値化する技術を完全図解 信頼性指標
【図解】MTBFとMTTFの違い|"修理できるか"で使い分ける2つの指標 故障率曲線
【完全図解】故障率曲線(バスタブカーブ)|製品の"寿命"を3つの期間で理解する 品質保証
【QC検定1級】FMEA(故障モード影響解析)|リスクを数値化して優先対策
📖 信頼性工学シリーズ
- 信頼性工学とは?
- MTBFとMTTFの違い
- 故障率曲線(バスタブカーブ)
- アベイラビリティ(可用性)
- 信頼性ブロック図 ← 今ここ
- ワイブル分布(準備中)
- B10ライフ(準備中)
- 打ち切りデータ ← 次はこれ!
- ワイブル確率紙(準備中)
💡 信頼性ブロック図は、「つなぎ方を変えるだけで信頼度が劇的に変わる」ことを教えてくれる強力なツールです。
直列と並列を意識した設計で、信頼性の高いシステムを作りましょう!
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。