※本記事にはプロモーション（広告）が含まれています。
こんな疑問、ありませんか？
- 「故障データがあるけど、mとηをどう求めればいいの？」
- 「ワイブル確率紙って、どうやって使うの？」
- 「グラフィカル推定と最尤推定、どっちを使えばいい？」
○ この記事でわかること
- ワイブル確率紙とは何か、なぜ使うのか
- メジアンランク法で累積故障確率F(t)を求める方法
- 確率紙へのプロット手順（5ステップ）
- mとηの読み取り方を具体例で解説
- グラフィカル推定と最尤推定の違いと使い分け
結論（3秒で理解）
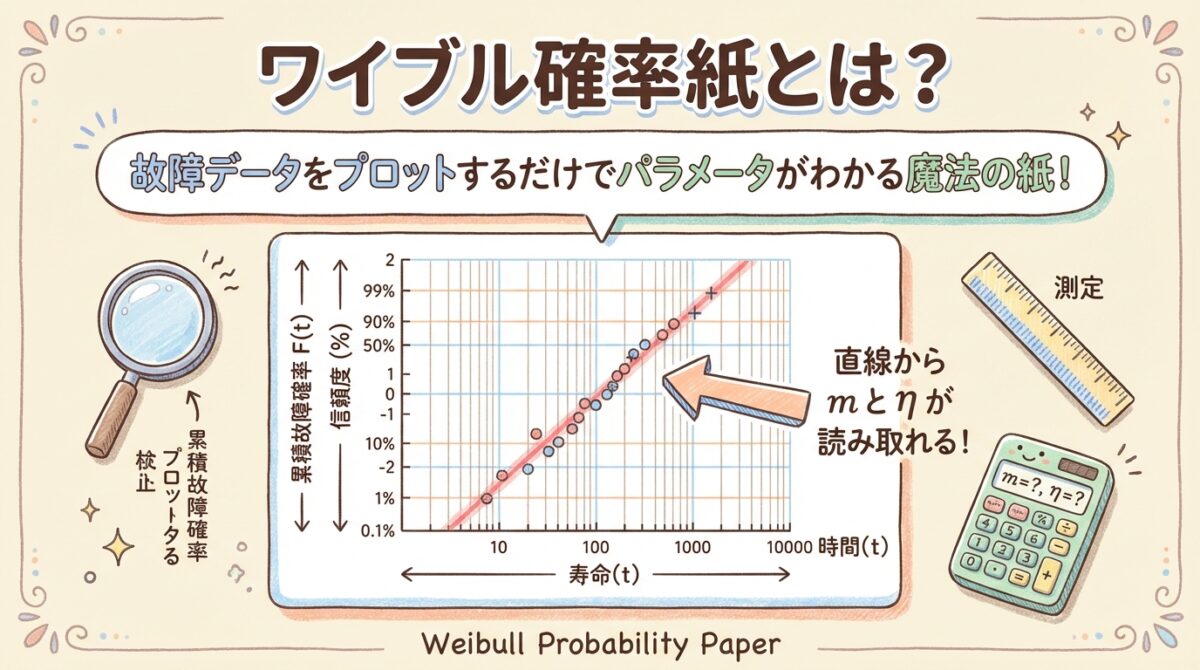
ワイブル確率紙は、故障データをプロットするだけでワイブル分布のパラメータ（m、η）を視覚的に読み取れる特殊なグラフ用紙です。
対数変換によって曲線が直線になるので、直線の傾きからm、F=63.2%の位置からηがわかります。
故障データを収集したら、次は「このデータはワイブル分布のどんなパラメータに対応するのか？」を知りたくなりますよね。
数式でゴリゴリ計算する方法（最尤推定）もありますが、ワイブル確率紙を使えば、データをプロットして直線を引くだけでmとηが求められます。
この記事では、ワイブル確率紙の使い方を図解たっぷり・具体例で解説します。
ワイブル確率紙とは？
ワイブル確率紙の定義
故障データがワイブル分布に従うとき、データをプロットすると直線になるように設計された特殊なグラフ用紙。
X軸：時間t（対数目盛）
Y軸：累積故障確率F(t)（特殊目盛）
別名：ワイブルプロット、Weibull probability paper
なぜ確率紙を使うのか？
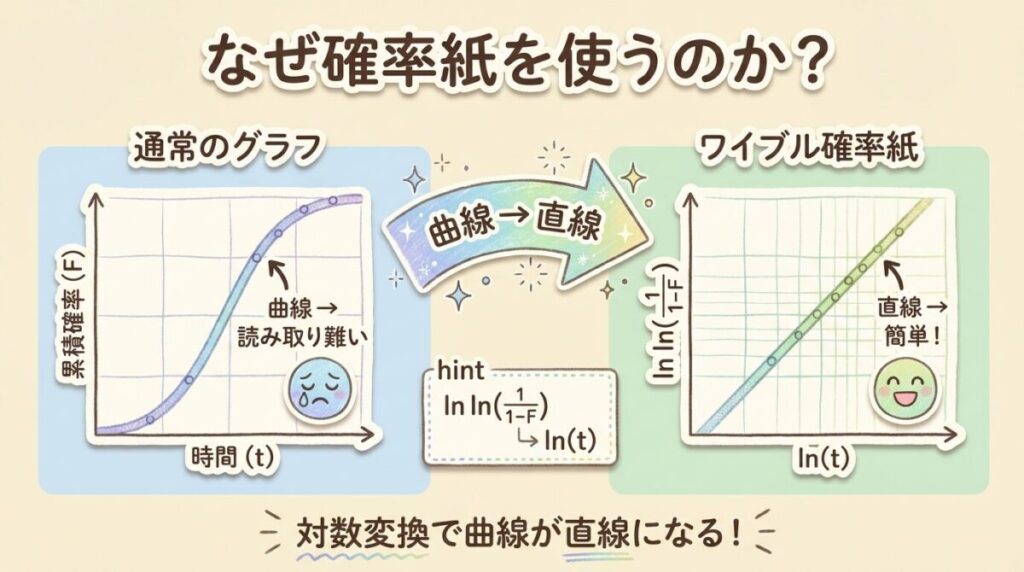
ワイブル分布の累積故障分布F(t)は曲線です。
曲線からパラメータを読み取るのは難しい…。
そこで、数学的な変換を使って曲線を直線に変えます。
曲線を直線に変える数学
ワイブル分布の累積故障分布：
F(t) = 1 − exp[−(t/η)m]
両辺を変形すると…
ln ln(1/(1−F)) = m・ln(t) − m・ln(η)
これは Y = m・X + b の形（直線の式）！
Y = ln ln(1/(1−F))、X = ln(t) とすれば直線になります。
普通のグラフ
・曲線になる
・パラメータが読み取りにくい
・目視での判断が難しい
ワイブル確率紙
・直線になる
・傾きからmが読める
・F=63.2%からηが読める
ワイブル確率紙の構造
X軸とY軸の読み方
X軸：時間 t（対数目盛）
故障時間をプロット。
対数目盛なので、10, 100, 1000…と等間隔に見える。
Y軸：累積故障確率 F(t)（特殊目盛）
ln ln(1/(1−F)) の変換が施された目盛。
1%, 5%, 10%, 50%, 63.2%, 90%, 99% などが表示される。
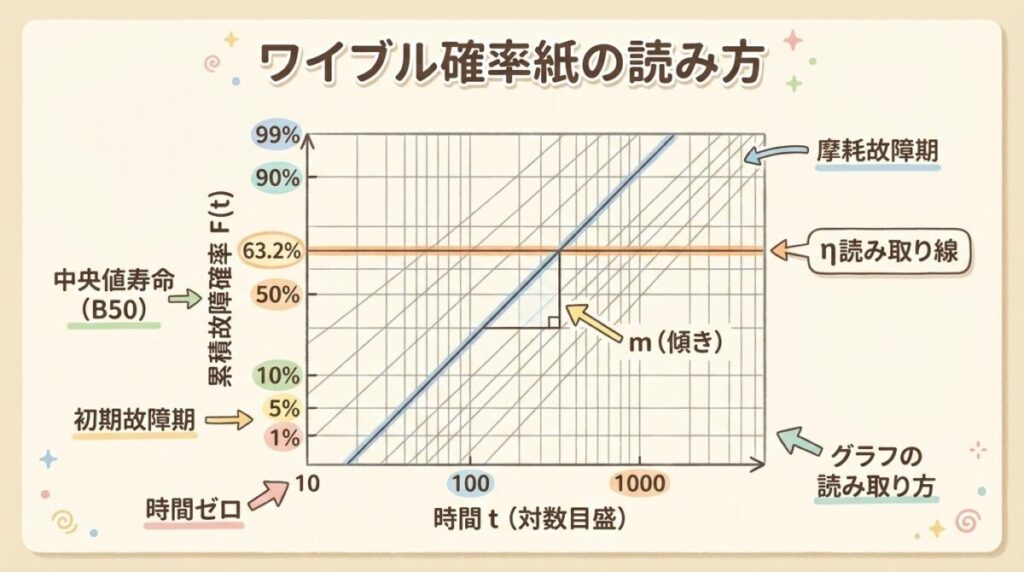
63.2%ラインが超重要！
Y軸のF = 63.2%の位置は特別な意味を持ちます。
直線がこのラインと交わる点のX座標がη（特性寿命）です。
なぜ63.2%？ → ワイブル分布でt=ηのとき、F(η) = 1 − 1/e ≈ 0.632 だから。
パラメータの読み取り方
| パラメータ | 読み取り方 | 意味 |
|---|---|---|
| η（イータ） | F=63.2%のラインと直線の交点のX座標 | 特性寿命（約63%が故障する時間） |
| m | 直線の傾き（専用の目盛で読み取る） | 形状パラメータ（故障パターン） |
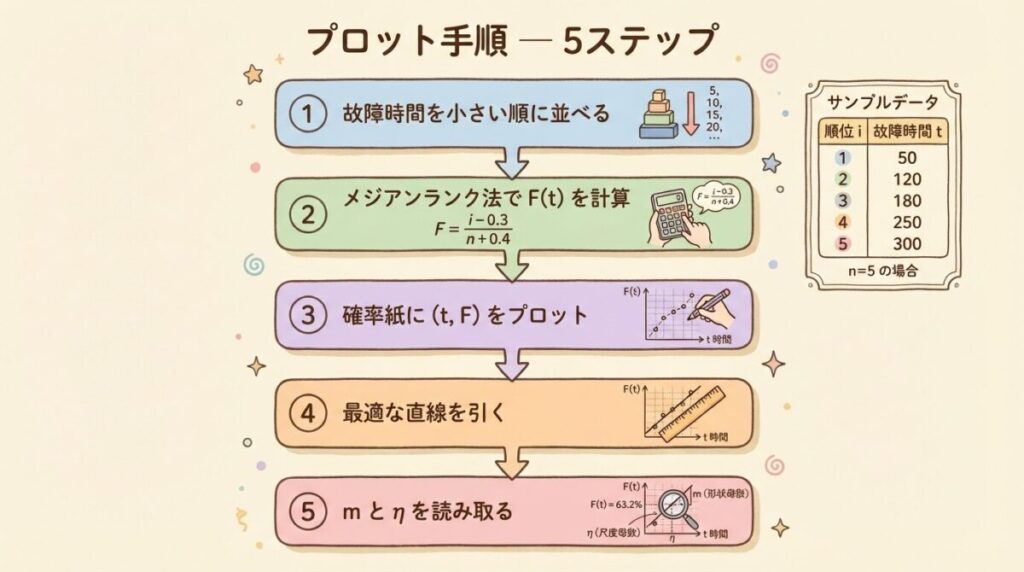
プロット手順（5ステップ）
故障データからワイブルパラメータを求める手順を、順番に見ていきましょう。
Step 1：故障時間を小さい順に並べる
収集した故障データを昇順（小→大）にソートします。
例：100, 200, 350, 500, 800時間
Step 2：メジアンランク法でF(t)を計算
各故障時間に対応する「累積故障確率」を計算します。
（詳細は後述）
Step 3：確率紙に (t, F) をプロット
X軸に故障時間t、Y軸に累積故障確率F(t)をプロット。
Step 4：最適な直線を引く
プロットした点を通る「最もそれらしい直線」を引きます。
目視または最小二乗法で。
Step 5：mとηを読み取る
直線の傾きからm、F=63.2%との交点からηを読み取ります。
メジアンランク法とは？
Step 2の「累積故障確率F(t)」を求める方法です。
「i番目に故障したとき、全体の何%が故障しているか」を推定します。
メジアンランク法の公式
F(i) = (i − 0.3) / (n + 0.4)
i = 故障順位（1, 2, 3, ...）、n = 総サンプル数
なぜ単純に i/n ではないのか？
補正が必要な理由
単純に i/n とすると、最後のデータ（i=n）で F=100% になってしまいます。
でも、「n個中n個が故障した」からといって、真の累積故障確率が100%とは限りません。
たまたま早く壊れた可能性もあります。
メジアンランク法の (i−0.3)/(n+0.4) は、統計的に最も妥当な推定値を与える補正式です。
他のランク推定法
| 方法 | 公式 | 特徴 |
|---|---|---|
| メジアンランク | (i−0.3)/(n+0.4) | 最も一般的 |
| ミーンランク | i/(n+1) | 計算が簡単 |
| 対称CDF | (i−0.5)/n | 対称分布向け |
計算例：実際にやってみよう
例題
5個のベアリングを同時に稼働させたところ、以下の時間で故障した。
ワイブルパラメータ（m, η）を推定しなさい。
故障時間：100, 200, 350, 500, 800時間
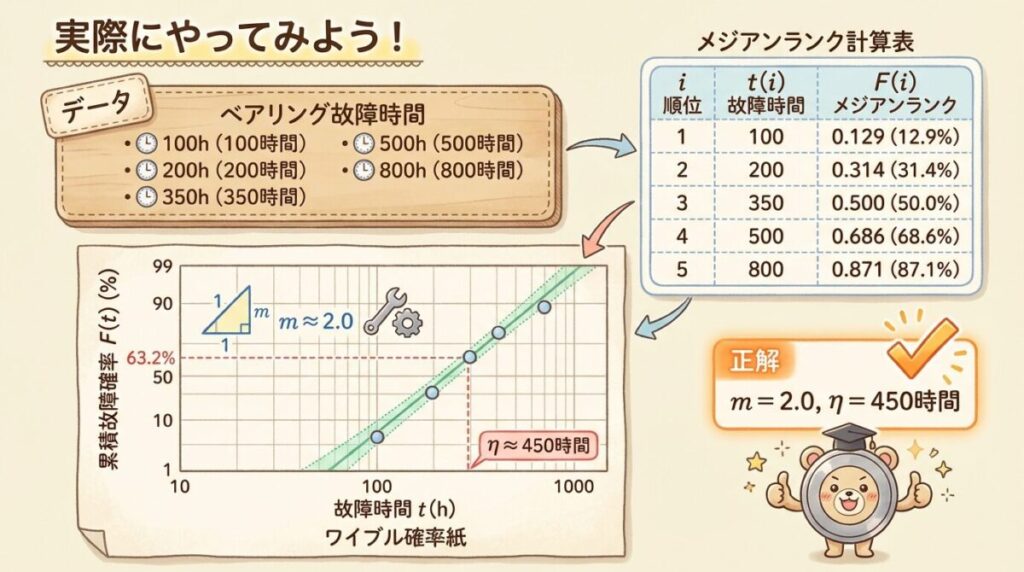
Step 1 & 2：データ整理とF(t)の計算
メジアンランク法 F(i) = (i − 0.3) / (n + 0.4) を使って計算します。
n = 5 なので、分母は 5 + 0.4 = 5.4 です。
| 順位 i | 故障時間 t（時間） | 計算式 | F(i)（%） |
|---|---|---|---|
| 1 | 100 | (1−0.3)/5.4 | 13.0% |
| 2 | 200 | (2−0.3)/5.4 | 31.5% |
| 3 | 350 | (3−0.3)/5.4 | 50.0% |
| 4 | 500 | (4−0.3)/5.4 | 68.5% |
| 5 | 800 | (5−0.3)/5.4 | 87.0% |
Step 3 & 4：プロットと直線引き
ワイブル確率紙に5点をプロットし、最適な直線を引きます。
5点の X＝ln t と Y＝ln ln(1/(1−F)) の値は、後の「確率紙がなくても計算で求められる」の表にまとめています。
5点が概ね直線上に並んでいれば、
データがワイブル分布に従っていることが確認できます。
Step 5：パラメータの読み取り
η（特性寿命）の読み取り
直線とF = 63.2%のラインとの交点を見ます。
この例では、交点のX座標は約450時間。
→ η ≈ 450時間
m（形状パラメータ）の読み取り
直線の傾きから読み取ります。
確率紙の右側や上側にある「m読み取り目盛」を使う方法もあります。
この例では、傾きから m ≈ 1.2
○ 推定結果
m ≈ 1.2（偶発故障に近いパターン）
η ≈ 450時間（約63%が故障する時間）
結果の解釈
m ≈ 1.2 は m = 1 に近いので、偶発故障型に近いパターン。
ただし、m > 1 なので、わずかに摩耗の傾向も見られます。
η ≈ 450時間 なので、B10ライフは…
B10 = 450 × [0.1054]1/1.2 ≈ 450 × 0.153 ≈ 69時間
つまり、約69時間で10%が故障すると予測できます。
確率紙がなくても計算で求められる｜最小二乗法とExcel
ワイブル確率紙は、縦軸を Y＝ln ln(1/(1−F))、横軸を X＝ln t に目盛った用紙です。つまり、この2つを計算して直線を当てはめれば、確率紙がなくても m と η が求まります。上の例題の5点で計算します。
| 故障時間 t | F（メジアンランク） | X＝ln t | Y＝ln ln(1/(1−F)) |
|---|---|---|---|
| 100 | 0.130 | 4.605 | −1.974 |
| 200 | 0.315 | 5.298 | −0.973 |
| 350 | 0.500 | 5.858 | −0.367 |
| 500 | 0.685 | 6.215 | 0.145 |
| 800 | 0.870 | 6.685 | 0.714 |
手順1 傾き：X と Y で直線 Y＝mX＋b を最小二乗法で当てはめると、傾き m≒1.28、切片 b≒−7.84
手順2 η：Y＝0（F＝63.2%）になる X は −b/m≒6.12 なので、η＝e^6.12≒453時間
手順3 B10：B10＝η×(ln(1/0.9))^(1/m)＝453×0.1054^(1/1.28)≒78時間
目で直線を引いた読み取り（m≈1.2、η≈450時間）と、ほぼ同じ値になりました。Excel なら、X と Y の列を作り、傾きは SLOPE(Yの範囲, Xの範囲)、切片は INTERCEPT(Yの範囲, Xの範囲) で求められます。散布図に近似直線を入れても同じ傾きが表示されます。
確率紙＝縦軸 ln ln(1/(1−F))・横軸 ln t のグラフ。直線の傾きが m、η＝exp(−切片÷m)。Excel の SLOPE と INTERCEPT で計算できる。
よくある質問
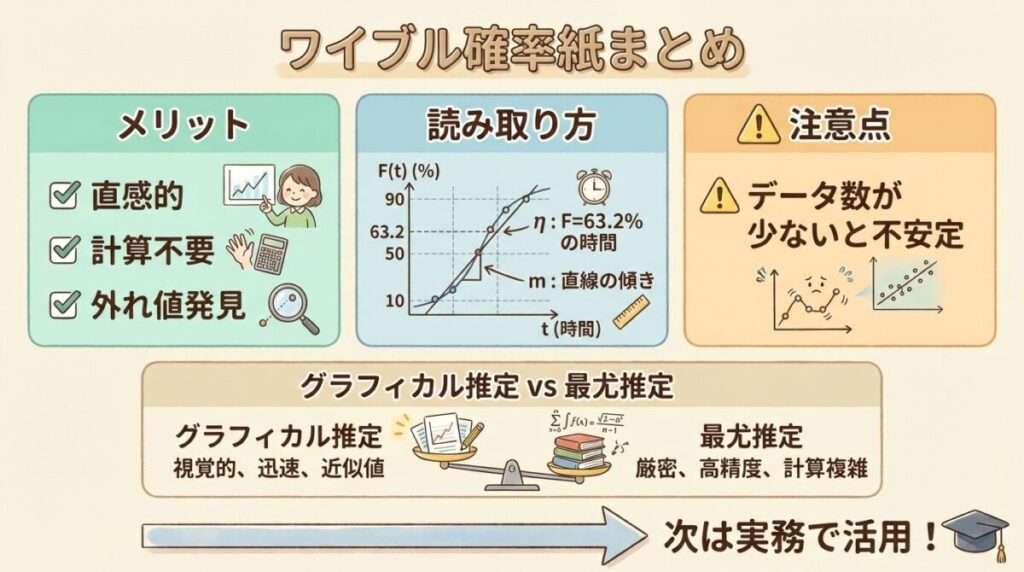
グラフィカル推定 vs 最尤推定
ワイブルパラメータの推定方法は、大きく分けて2つあります。
| 項目 | グラフィカル推定 （確率紙） |
最尤推定 （MLE） |
|---|---|---|
| 方法 | 確率紙にプロット→直線を引く | 尤度関数を最大化する数値計算 |
| 計算 | 手計算・目視で可能 | コンピュータが必要 |
| 精度 | 主観が入る、やや低い | 数学的に最適 |
| 直感性 | データの傾向が見える | ブラックボックス |
| 外れ値発見 | 直線から外れた点がすぐわかる | 別途分析が必要 |
| おすすめ場面 | 初期分析、データの概観把握 | 厳密な推定、報告書作成 |
実務での使い分け
① まずグラフィカル推定でざっくり把握
→ データがワイブル分布に従うか？外れ値はないか？
② 次に最尤推定で厳密な値を計算
→ 報告書や設計計算には最尤推定の結果を使う
両方使うのがベストプラクティスです！
まとめ
○ この記事のポイント
- ワイブル確率紙は、故障データをプロットすると直線になる特殊なグラフ用紙
- メジアンランク法でF(t)を計算：F(i) = (i − 0.3) / (n + 0.4)
- ηの読み取り：直線とF=63.2%ラインの交点のX座標
- mの読み取り：直線の傾き
- グラフィカル推定→最尤推定の順で使うのがベスト
ワイブル確率紙の使い方（5ステップ）
- 故障時間を小さい順に並べる
- メジアンランク法でF(t)を計算
- 確率紙に (t, F) をプロット
- 最適な直線を引く
- mとηを読み取る
ワイブル確率紙を使えるようになったら、「打ち切りデータ」の扱い方も押さえておきましょう。
実際の寿命試験では、すべてのサンプルが故障する前に試験を終えることが多いです。
ワイブル確率紙は、「故障データを直線で見える化する」強力なツールです。
まずはプロットしてみて、データの「傾向」を目で確認する習慣をつけましょう！
読み取った m の値で、初期故障・偶発故障・摩耗故障のどれかがわかります。ワイブル分布の見方を確かめられます。
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ（シグマ）や ∫（インテグラル）を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ（意味）』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる！最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点（何点分出るか）」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。
ポチップ
品質管理を、教科書で基本から学び直したいときに向いています。品質管理の基本をわかりやすく解説した教科書です（第5版）。
QC検定1級を目指すなら、出題範囲に沿ったテキストで全体を押さえておくと安心です。QC検定1級の受検テキストです（日科技連出版社）。
「ワイブル確率紙」の土台になる確率・統計の考え方を、信頼性工学の教科書で確かめたいときに向いています。確率・統計の考え方を信頼性に当てはめて解説した、信頼性工学の入門書です（森北出版、福井泰好 著、第2版）。
メーカーで電気設計と品質保証に携わってきた経験をもとに執筆しています。むずかしい専門用語をできるだけ使わず、はじめて学ぶ人がつまずかないように、図とたとえで説明することを大切にしています。
次に読むべき記事
この記事の内容がわかったら、信頼性工学の次のテーマに進みましょう。続けて読むと、現場でそのまま使える知識になります。
テーマ別に、もっと深く学ぶ
気になるところから読んでも大丈夫です。どの記事も、はじめて学ぶ人向けにやさしく書いています。
