目次
💭 こんな疑問、ありませんか?
「正規分布って何?なんでこんなに重要なの?」
「68-95-99.7って何の数字?」
「z得点って何に使うの?」
✅ この記事を読めば、統計の王様「正規分布」が完璧に理解できます!
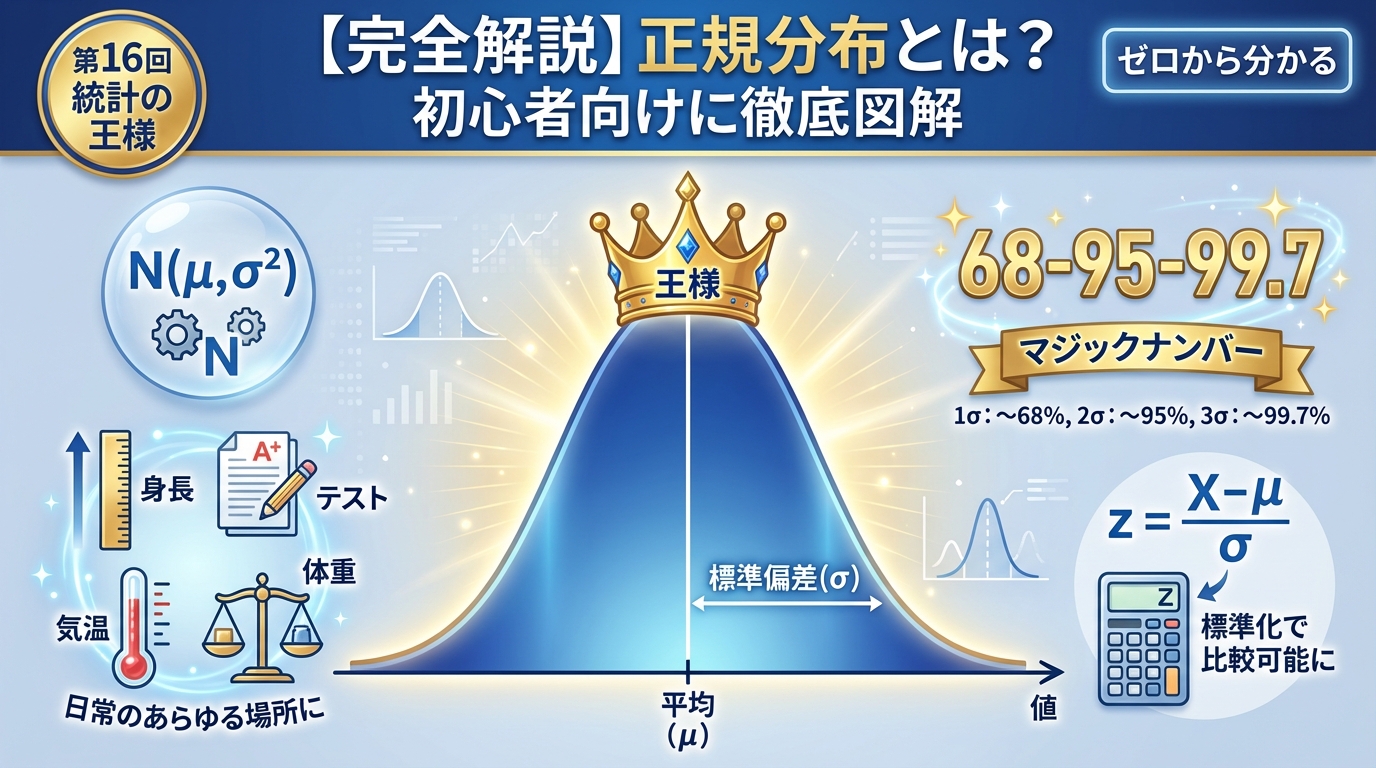
🎯 正規分布とは?なぜ「王様」なのか
正規分布は、「真ん中が一番多くて、端っこほど少ない釣鐘型」の分布です。
統計学では「王様」と呼ばれるほど重要で、身の回りのあらゆるデータがこの形になります。
👑 なぜ「王様」と呼ばれるのか?
- 最も頻繁に現れる: 自然界の多くの現象が正規分布に従う
- 計算がしやすい: 数学的な性質が美しく、理論が発達している
- 実用性が高い: 成績評価、品質管理、リスク分析など、あらゆる分野で活用される
- 予測に使える: 将来の値を統計的に予測できる
📊 日常生活で見つける正規分布
🏫 学校生活で
- クラスメイトの身長: 平均付近が多い、極端に高い・低い人は少ない
- テストの点数: 真ん中の点数が多い、満点・0点は稀
- 体重測定: 平均体重付近に集中
- 通学時間: だいたい同じくらい、極端に早い・遅いは少ない
💡 なぜこうなる?
例えば身長は、遺伝、栄養、運動、睡眠などたくさんの要因が組み合わさった結果です。
このように多数の要因が影響すると、自然と正規分布の形になります。これを「中心極限定理」と呼びます(後ほど詳しく解説!)。
🔔 正規分布の3つの特徴
特徴① 平均付近が最も多い
釣鐘の頂点が平均値で、そこに最も多くのデータが集まります。
例: 身長170cmが平均なら、170cm付近の人が最も多い。
特徴② 完全に左右対称
平均を中心に左右が鏡のように対称です。
例: 平均より10cm高い人の数 = 平均より10cm低い人の数
特徴③ 極端な値は非常に稀
平均から大きく離れた値はほとんど出現しません。
例: 平均身長170cmなら、2m超えや140cm未満は極めて稀。
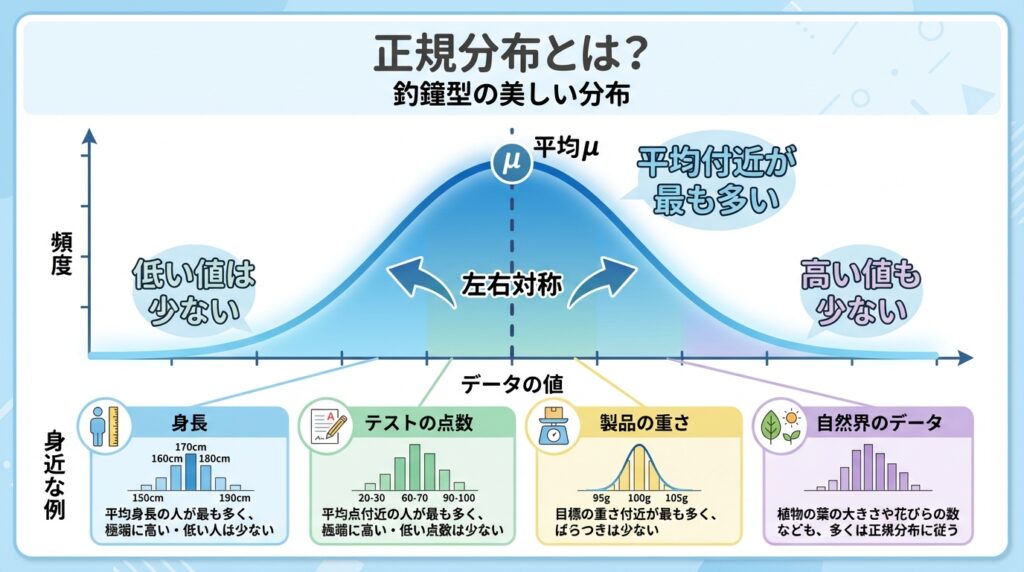
✨ 68-95-99.7ルール: 魔法の数字
正規分布を理解するうえで最も重要なのがこの「68-95-99.7ルール」です。
この3つの数字さえ覚えれば、どんな正規分布でも理解できます!
📐 68-95-99.7ルールとは?
📏 具体例で理解: 身長分布
💡 設定条件
成人男性の身長: 平均170cm、標準偏差6cm
ステップ① 各範囲を計算
- 1標準偏差: 170 ± 6 = 164cm〜176cm
- 2標準偏差: 170 ± 12 = 158cm〜182cm
- 3標準偏差: 170 ± 18 = 152cm〜188cm
ステップ② 人数の割合を理解
📝 もう一つの例: テストの点数
💡 設定条件
数学のテスト結果: 平均70点、標準偏差10点
計算結果
- 68%の生徒: 60点〜80点(標準的な成績)
- 95%の生徒: 50点〜90点(普通の範囲)
- 99.7%の生徒: 40点〜100点(ほぼ全員)
- 上位2.5%: 90点以上(優秀)
- 下位2.5%: 50点未満(要サポート)
📌 覚え方のコツ
- 68%: 「ロッパー(68)は標準」→ 約2/3が標準範囲
- 95%: 「救護(95)されるのはほぼ全員」→ ほとんどの人
- 99.7%: 「掘ればナナいけど(997)全員」→ ほぼ全員
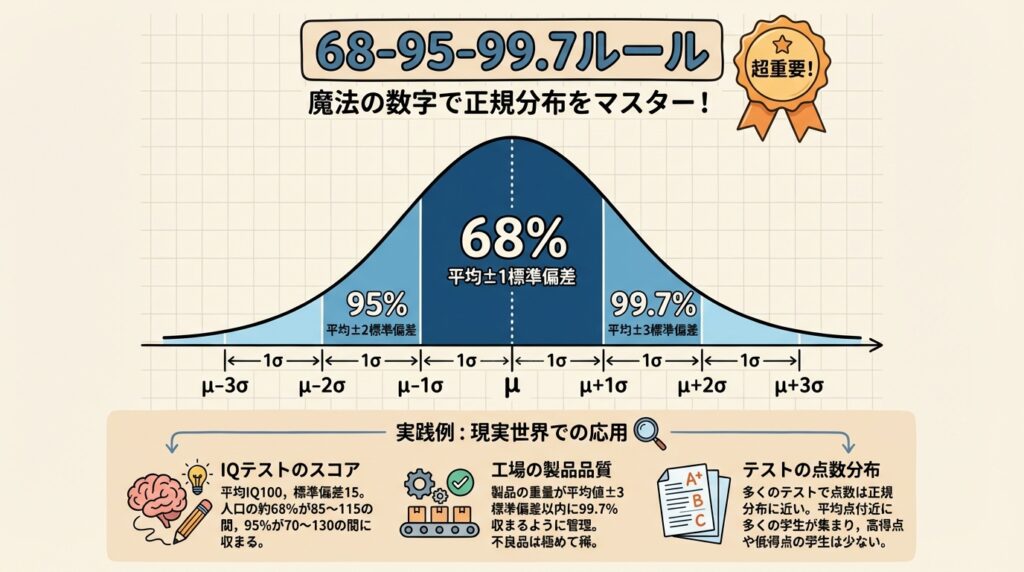
🔧 z得点(標準化): 異なるデータを比較する魔法
z得点は「平均からどれだけ離れているか」を標準偏差を単位として表した数値です。
これを使えば、単位が違うデータ同士でも比較できます!
📐 z得点の計算式
🎓 実践例: 成績比較
💡 問題設定
太郎くんの成績比較: どちらの科目が優秀?
- 数学: 80点(平均70点、標準偏差10点)
- 英語: 75点(平均60点、標準偏差15点)
ステップ① それぞれのz得点を計算
数学のz得点:
z = (80 - 70) / 10 = 1.0
英語のz得点:
z = (75 - 60) / 15 = 1.0
ステップ② 結果を解釈
両方ともz = 1.0 → 平均より1標準偏差上
✅ 結論: どちらも同じレベルの優秀さ!
📊 z得点の解釈表
💡 z得点の利点
- 異なる単位を比較可能: 身長(cm)とテストの点数を比較できる
- 相対的な位置が分かる: 集団の中での位置が一目瞭然
- 偏差値計算に使える: 偏差値 = 50 + 10×z
- 異常値の検出に便利: |z| > 3なら極端な値
📚 関連記事
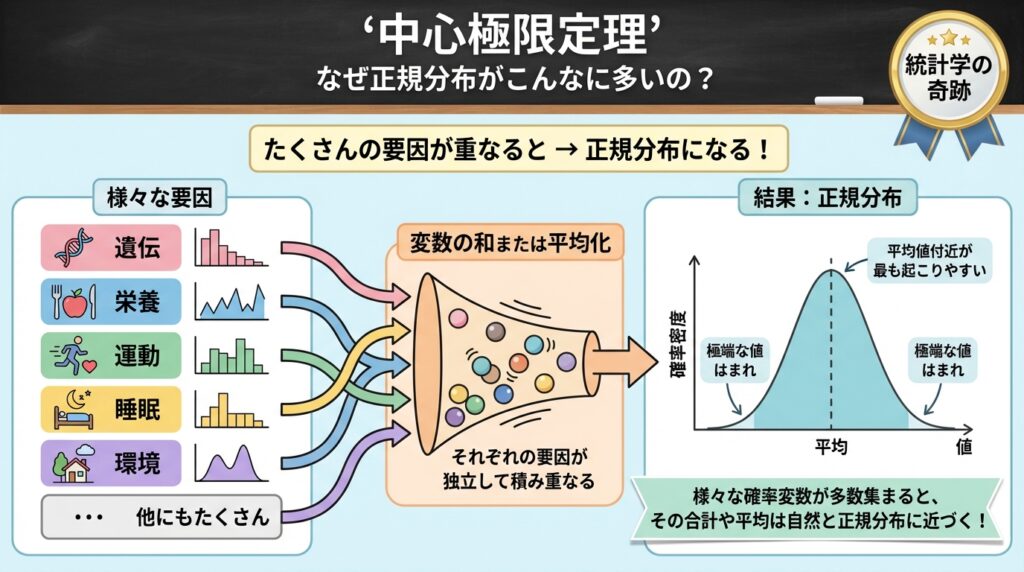
🌟 中心極限定理: なぜ正規分布がこんなに多いのか?
中心極限定理とは、「たくさんの要因が積み重なると、結果は正規分布になりやすい」という統計学の奇跡的な法則です。
これが、正規分布が「王様」と呼ばれる理由です!
🔬 中心極限定理を分かりやすく
たくさんの要因が重なる → 正規分布になる!
(要因が独立でなくても、多ければ正規分布に近づく)
📏 具体例: 身長が正規分布になる理由
💡 身長に影響する要因
- 遺伝的要因: 両親の身長、DNA
- 栄養状態: 幼少期の食事、栄養バランス
- 運動習慣: 成長期の活動量
- 睡眠時間: 成長ホルモンの分泌
- 病気の有無: 健康状態、慢性疾患
- ...など、多数の要因が組み合わさる
→ 結果として正規分布の形になる!
📝 もう一つの例: テストの点数
テストの点数に影響する要因
- 基礎学力: 計算能力、基本的な理解
- 勉強時間: 準備期間、復習の量
- 理解度: 概念の把握レベル
- 体調: 当日のコンディション
- 運の要素: 出題傾向との相性
- ...など、多数の要因が組み合わさる
→ 結果として正規分布の形になる!
🎲 サイコロ実験で体感!
サイコロの実験で、中心極限定理を実際に体感してみましょう。
実験: サイコロを複数個振った平均
🎲 1個の場合:
出る目: 1, 2, 3, 4, 5, 6(すべて同じ確率)
→ 均等分布(正規分布ではない)
🎲🎲 2個の平均:
平均1.0: (1,1)だけ → 1通り
平均3.5: 最も多い → 6通り
→ 三角形っぽい分布(少し正規分布に近づく)
🎲🎲🎲🎲 4個の平均:
平均3.5付近に集中
→ ほぼ正規分布の形!
🎲 × 10個の平均:
→ 完璧な正規分布!
📌 重要なポイント
- 要因(サイコロ)が多いほど正規分布に近づく
- 各要因は独立でなくてもOK
- 自然界の多くの現象が該当
- これが正規分布の普遍性の理由!
💼 実務での活用: 正規分布を使いこなす
正規分布は、学問だけでなく実務の様々な場面で活用されています。
🏫 場面① 学校の成績管理
👩🏫 先生の視点: クラスのテスト結果を分析
平均点75点、標準偏差12点の場合:
- 68%の生徒: 63〜87点(普通の成績)
- 95%の生徒: 51〜99点(想定範囲内)
- 上位2.5%: 87点以上(優秀)
- 下位2.5%: 63点以下(要サポート)
🏭 場面② 品質管理の現場
👨🏭 工場の品質管理担当者
目標重量100g、標準偏差2gの場合:
- 合格範囲: 94g〜106g(平均±3標準偏差)
- → 99.7%の製品が合格
- → 0.3%の製品が不良品
- 管理限界: 96g〜104g(平均±2標準偏差)
- → この範囲を外れたら工程調整
🏥 場面③ 医療現場での判定
👩⚕️ 健康診断での活用
収縮期血圧 平均120mmHg、標準偏差15mmHgの場合:
- 正常範囲(68%): 105〜135mmHg
- 注意範囲(95%): 90〜150mmHg
- 要治療(上位2.5%): 150mmHg超
- 低血圧(下位2.5%): 90mmHg未満
📚 まとめ: 正規分布は統計の王様
✅ この記事のポイント
- 正規分布とは?
真ん中が多く、両端が少ない釣鐘型の分布。自然界の多くの現象が従う。 - 68-95-99.7ルール
平均±1σに68%、±2σに95%、±3σに99.7%のデータが含まれる。 - z得点の計算
z = (X - μ) / σ で異なるデータを比較可能。偏差値 = 50 + 10×z - 中心極限定理
多数の要因が重なると正規分布になる。これが普遍性の理由。 - 実務での活用
成績評価、品質管理、医療判定など、あらゆる分野で使われる。
🎯 重要な公式まとめ
z得点の計算:
z = (X - μ) / σ
偏差値の計算:
偏差値 = 50 + 10 × z
68-95-99.7ルール:
- μ ± 1σ: 68%
- μ ± 2σ: 95%
- μ ± 3σ: 99.7%
📚 次に読むべき記事
🔰 統計学の基礎を固める
⚙️ 実践的な統計知識
💬 質問・コメント大歓迎です!
「この部分がよく分からない」「実際の現場ではどうなの?」など、お気軽にコメント欄で質問してください。できる限りお答えします!
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。