こんにちは、シラスです。
統計学を学んでいるとき、あるいは品質管理のデータ処理をしているとき、誰もが一度は抱く「疑問」があります。
「なぜ、分散を求めるときに n ではなく n−1 で割るのか?」
平均値を求めるときはデータの個数 n で割るのに、なぜ分散(不偏分散)のときだけ n−1 という中途半端な数字が登場するのでしょうか?
「教科書には『自由度が減るから』と書いてあるけど、意味がわからない」 「Excel関数も STDEV.P(n) と STDEV.S(n−1) があって、どっちを使えばいいか不安」
そんな方のために、今日は数式証明を一切使わず、「なぜ1引く必要があるのか?」を直感的なイメージだけで解説します。
目次
1. 結論:nで割ると「小さく見積もってしまう」から
まずは結論から入ります。 私たちが n−1 で割る(分母を少し小さくする)理由は、計算結果を「少し大きく補正したいから」です。
なぜ補正が必要なのでしょうか?
本来のバラつき(母分散)よりも「狭く、小さく」見えてしまう性質がある。
だからどうする?
「分母を n-1 に減らして、計算結果を少し大きく膨らませることで、真の値に近づける!」
つまり、「そのままだと小さくなりすぎるから、ちょっとズルをして大きくしている」というのが、不偏分散の実態です。
では、なぜ「小さく見えてしまう」のでしょうか? ここが一番のポイントです。
2. 「自分の都合の良い平均値」を使う罠
私たちが分散を計算するとき、まず「平均値」を求め、そこからの「ズレ(偏差)」を計算しますよね?
実は、ここに大きな落とし穴があります。
- 本当の基準: 真の平均値(母平均 μ)
- 私たちが使う基準: 手元のデータだけの平均値(標本平均 xˉ)
私たちは「真の平均値」を知らないので、仕方なく「手元のデータの平均値」を基準にしてバラつきを計算します。 しかし、手元のデータから計算した平均値は、そのデータたちにとって「最も居心地が良い(距離が近い)場所」に発生します。
図解:3人の待ち合わせ
イメージしやすいように、広い公園(母集団)にいる3人(サンプル)で考えてみましょう。
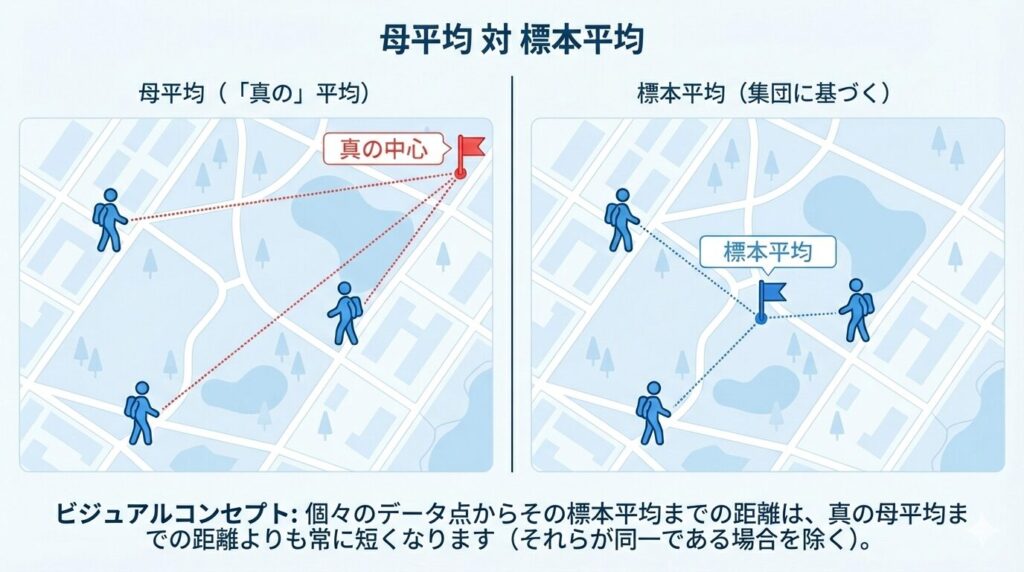
- 真のバラつき(対:公園の中心) 公園の中心(母平均)から、3人がどれくらい離れているかを知りたい。これが本当の分散です。3人は公園の端っこに集まっているかもしれません。
- 計算上のバラつき(対:3人の重心) でも、私たちは公園の中心を知りません。だから、「3人の真ん中(標本平均)」を基準にして、そこからの距離を測ります。
当然、「3人の真ん中」から測った距離のほうが、「公園の中心」から測るよりも短くなりますよね? 自分たちで作った中心(標本平均)なんだから、自分たちに近いのは当たり前です。
手元のデータだけで平均を作ると、データはその平均の周りに「こじんまり」と集まってしまう。
その結果、計算されるバラつきは、本来のバラつきよりも必ず小さくなる(過小評価)。
この「小さくなってしまった分」を補正するために、あえて n ではなく n−1 で割って、数値を少し大きくしてあげるのです。
3. n と n−1 の差は「データ数」で変わる
この「補正」の影響力は、データ数(n)が少ないときほど大きく、データ数が多いと小さくなります。 これも直感と一致します。
ケースA:データが少ない時(n=3)
3人だけの平均値は、かなり彼らに寄り添った(偏った)場所にあります。過小評価の度合いが激しいです。
- n で割るのと、n−1(つまり2)で割るのでは、結果が 1.5倍 も変わります。
- だから、しっかり n−1 で補正しないと危険です。
ケースB:データが多い時(n=1000)
1000人もいれば、その平均値は「真の平均値」にかなり近づきます。過小評価のズレは微々たるものです。
- 1000で割るのと、999で割るのでは、結果は 0.1% しか変わりません。
- データが十分にあれば、n でも n−1 でも、実はどっちでも良くなります。
「統計学はデータが少ないときほど厳密さが求められる」と言われるのはこのためです。
4. 自由度(Degrees of Freedom)の話
最後に、少しだけ専門的な「自由度」の話をします。 教科書によくある「平均値を決めるのに情報を1つ使ってしまったから、自由に動けるデータは n−1 個だ」という説明です。
これも直感で理解できます。
例えば、「3つの数字の平均が5」だと決まっていたとします(平均値を固定)。
- 1つ目の数字は「2」です。(自由に決めてOK)
- 2つ目の数字は「8」です。(自由に決めてOK)
- 3つ目の数字は……?
平均を5にするためには、3つ目は自動的に「5」にならざるを得ません。 もう自由はありませんよね。
私たちが分散を計算するとき、「標本平均 xˉ」を使った時点で、データのうちの1つは「辻褄合わせ」のために自由を失っているのです。 だから、有効な情報の数は n ではなく n−1 (自由度)として扱います。
こちらの考え方については以下の記事で詳しく解説してますのでぜひ見てください。
まとめ:n-1 は「優しさ」である
分散の分母が n−1 になっている理由、スッキリしましたか?
- 標本平均を使うと、データが中心に集まりすぎて、バラつきを過小評価してしまう。
- その「小さくなった分」を元に戻すために、分母を小さくして(n−1)、値を膨らませている。
つまり、不偏分散の n−1 は、数式の難解なルールではなく、「少ないデータで真実を知ろうとする私たちへの補正(優しさ)」なのです。
実務で Excel を使うときは、手元のデータが全数(母集団そのもの)でない限り、基本的には STDEV.S(不偏標準偏差:n-1) を選んでおけば間違いありません。
この「ちょっとしたズレ」を意識できるかどうかが、データ分析のセンスを分けます。
より実践的な自由度の扱いについては以下の記事を読んでみてください!

