こんにちは、シラスです。
これまで、キズの数や事故件数などの「不適合数(ポアソン分布)」について、Z検定(正規分布)を使って検定してきました。
しかし、いざ「来月の事故件数は、何件〜何件の間になるか?」を予測しようとすると、統計学の教科書には奇妙なことが書かれています。
「不適合数の区間推定には、カイ二乗分布 ($\chi^2$) を使いなさい」
「えっ? カイ二乗って『バラつき(分散)』を見るための分布だよね? なんで『回数』の予測に出てくるの?」
多くの人がここで混乱します。
今日は、この統計学のミステリーを解き明かしつつ、ポアソン分布の信頼区間を計算する手順を解説します。
目次
1. なぜ「カイ二乗分布」が登場するのか?
結論から言うと、「ポアソン分布とカイ二乗分布は、実は親戚(数学的に同じ形)」だからです。
少しイメージの話をしましょう。
- ポアソン分布: 「ランダムに発生するイベント(事故など)の回数」を表す。
- カイ二乗分布: 「ランダムなズレ(標準正規分布)を二乗して足し合わせたもの」を表す。
実は、ポアソン過程(ランダムな発生)における「イベントが発生するまでの待ち時間」は指数分布に従い、それを積み重ねていくとガンマ分布になり…と数式変換していくと、最終的に「自由度 $2\lambda$ のカイ二乗分布」と同じ形になることが証明されているのです。
理屈は難しいですが、実務で覚えるべきルールは1つだけです。
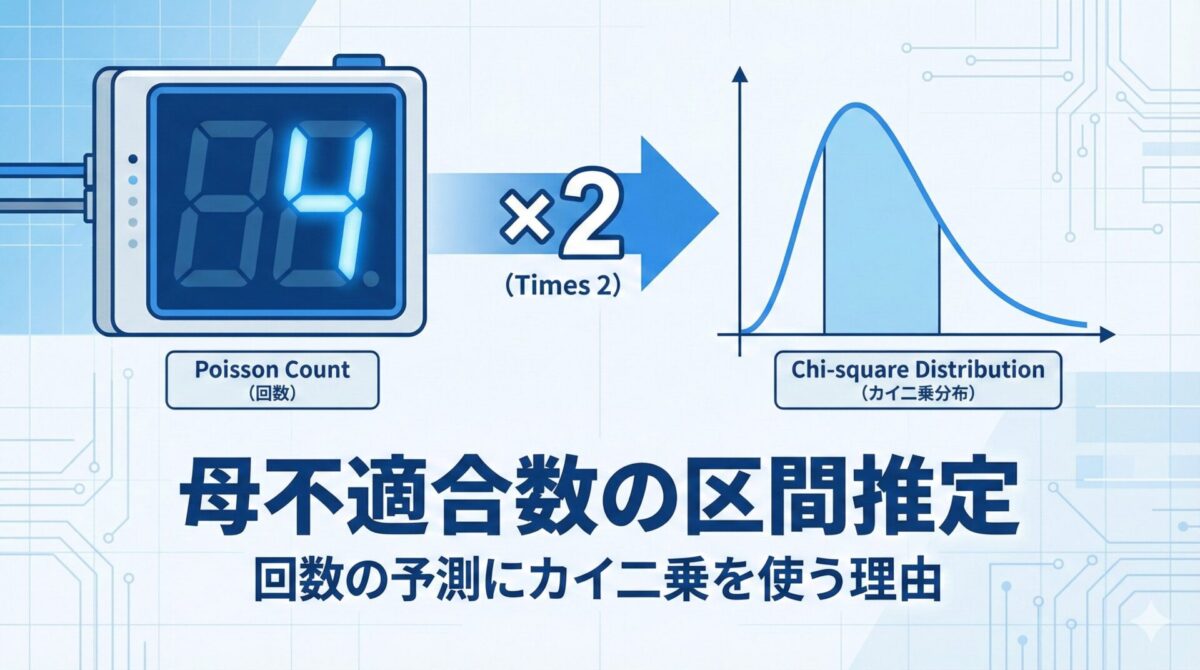
「回数($c$)を2倍すると、カイ二乗分布の自由度として使える!」
2. 計算式:回数を「2倍」して表を引く
母不適合数 $\lambda$ の信頼区間を求める公式は、以下の通りです。
何やら複雑そうですが、ポイントは「自由度($\phi$)の決め方」だけです。
- 下限の自由度 $\phi_L$: $2 \times c$
- 上限の自由度 $\phi_U$: $2 \times (c+1)$
「観測した回数($c$)を2倍する」。
そして、表から読み取ったカイ二乗値を「半分($1/2$)にする」。
これだけで、真の発生数($\lambda$)の範囲が求まります。
3. 実践:事故件数のリスク予測
具体的なデータで計算してみましょう。
ある工場で、先月の労働災害(ヒヤリハット含む)は $c = 4$ 件 でした。
「この工場の潜在的な事故発生率(母不適合数 $\lambda$)は、95%の確率で何件〜何件の間にあるか?」
ステップ1:自由度を決める
観測数 $c=4$ なので、
- 下限用: $\phi_L = 2 \times 4 = \mathbf{8}$
- 上限用: $\phi_U = 2 \times (4+1) = \mathbf{10}$
ステップ2:カイ二乗分布表を見る
95%信頼区間なので、分布表の「右側2.5%(0.025)」と「左側97.5%(0.975)」の値を探します。
- 下限用(自由度8, 左側): $\chi^2(8, 0.975) = \mathbf{2.18}$
- 上限用(自由度10, 右側): $\chi^2(10, 0.025) = \mathbf{20.48}$
ステップ3:半分にして範囲を出す
最後に、表の値を2で割ります。
- 下限: $2.18 \div 2 = \mathbf{1.09}$
- 上限: $20.48 \div 2 = \mathbf{10.24}$
答え: $1.09 \le \lambda \le 10.24$
4. 結果の解釈:「たまたま4件」の裏側
この結果は、恐ろしい事実を示唆しています。
「先月はたまたま4件で済んだけど、この工場の実力値(リスク)としては、最大で月10件ペースで事故が起きてもおかしくない状態だよ」
たった4件のデータからでも、カイ二乗分布を使うことで、これだけ幅を持った(安全サイドの)リスク評価ができるのです。
特に、発生数が少ない($c=0$や$1$)の時ほど、この区間推定は威力を発揮します。
「0件だったからヨシ!」ではなく、「上限値は3.7件だから油断するな!」と言えるようになるからです。
まとめ
これで「計数値(比率・回数)」の検定・推定シリーズは全て完了です。
- 比率(%)なら正規分布。
- 回数(個)ならポアソン分布(推定はカイ二乗)。
この使い分けができれば、QC検定や実務のデータ分析で迷うことはもうありません。
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。