📊 こんな状況、ありませんか?
- 総平方和(ST)は計算できた…でも、これだけじゃ意味がわからない
- 「群間」「群内」って何が違うの?
- データのバラつきが「効果」なのか「誤差」なのか知りたい!
こんにちは、シラスです。
前回、実験データ全体のバラつきである「総平方和(ST)= 28」を計算しました。
しかし、この「28」という数字だけを見ても、実験が成功したのか失敗したのかは分かりません。
🎯
効果(シグナル)
温度を変えたから
データが良くなった?
この2つがごちゃ混ぜになっているからです。
今日は、この塊(ST)を、手術用メスのように鋭い計算式を使って、「効果(SA)」と「誤差(Se)」の2つにきれいに切り分けます。
✅ この記事で学べること
- 分解のイメージ:塾のクラスのテストの点数でイメージを掴む
- 群間平方和(SA):「効果」の計算方法
- 群内平方和(Se):「誤差」の計算方法(引き算で一発!)
- 結果の解釈:シグナルとノイズの比率を見る
目次
結論:全体を「効果」と「誤差」に分ける
最初に結論をお伝えします。
🔪 分解の公式
ST = SA + Se
|
28 全体 |
= |
24 効果 |
+ |
4 誤差 |

1. 分解のイメージ:「テストの点数」
計算に入る前に、「何を分けようとしているのか」をイメージで掴みましょう。
🏫 塾の2クラスで考える
ある塾で、AクラスとBクラスの生徒のテストの点数を比べるとします。
📝 生徒全員の点数のバラつき(ST)は、
以下の2つの理由で起きています。
① 先生の教え方の違い(SA)
「Aクラスの先生は教え方が上手いから、クラス全体の平均点が高いよね」
= 実験の効果(シグナル)
② 生徒個人の実力差(Se)
「同じクラスの中でも、できる子とできない子がいるよね」
= 偶然の誤差(ノイズ)
実験計画法の目的は、全体のバラつきの中から①(先生の実力)だけを抽出することです。
もし①が大きければ、「この先生の教え方には効果がある!」と証明できます。
🎂 ケーキで考える(前回の続き)
前回、総平方和を「ホールケーキ」にたとえました。
今日はそのケーキを2つに切り分けます。
🍫
チョコレート部分
= SA(効果)
24
🍰
スポンジ部分
= Se(誤差)
4
📐 分解の公式
ST = SA + Se
全体(ホールケーキ)= 効果(チョコ部分)+ 誤差(スポンジ部分)
📻 ラジオのノイズで考える
もう一つ、ラジオでたとえてみましょう。
ラジオから聞こえる音には、2種類あります。
🎵
シグナル(信号)
聞きたい音楽や声
= SA(効果)
📢
ノイズ(雑音)
ザーザーという雑音
= Se(誤差)
シグナルが大きくてノイズが小さいほど、音楽がクリアに聞こえる!
実験も同じです。効果(シグナル)が大きくて誤差(ノイズ)が小さいほど、「実験成功」と言えます。

2. 群間平方和(SA)の計算
では、具体的な計算に入りましょう。
まずは主役である「効果(SA)」を計算します。
🤔 「群間」ってなに?
「群」とは「グループ」のこと。
群間 = グループとグループの間(Between Groups)
つまり、「低温グループ」と「高温グループ」の平均の差によるバラつきです。
定義は「各水準の平均値と、全体平均とのズレ」ですが、実務では以下の「一発公式」を使います。
📐 群間平方和(SA)の公式
SA = ( T₁²/n₁ + T₂²/n₂ + … ) − CT
📝 計算手順(3ステップ)
各グループの合計(T)を二乗して、人数(n)で割る
それらを全部足す
最後に修正項(CT)を引く
🏭 実践計算(前回のデータ)
前回のデータ(プラスチック強度)を使います。
📝 計算してみよう
ステップ1:各グループの T²/n を計算
低温グループ:12² ÷ 3 = 144 ÷ 3 = 48
高温グループ:24² ÷ 3 = 576 ÷ 3 = 192
ステップ2:全部足す
48 + 192 = 240
ステップ3:CTを引く
SA = 240 − 216 = 24
🎉 SA = 24
これが「温度を変えたこと(先生の違い)によって生まれたズレのエネルギー」です。
ケーキで言えば、チョコレート部分の重さが「24」だと分かりました!

3. 群内平方和(Se)の計算
次に、残りの「誤差(Se)」を計算します。
🤔 「群内」ってなに?
群内 = グループの内側(Within Groups)
つまり、「同じ温度条件なのに、データがバラついている部分」=偶然の誤差です。
本来なら「各データと、そのグループ平均とのズレ」を計算するのですが、そんな面倒なことはしません。
なぜなら、私たちはすでに「全体(ST)」と「効果(SA)」を知っているからです。
🎯 裏ワザ:引き算で一発!
📐 群内平方和(Se)の公式
Se = ST − SA
全体から効果を引けば、残りは全部「誤差」!
「全体から、分かっている効果を引けば、残りは全部ノイズ(個人の実力差)だよね」という考え方です。
これが一番早くて正確です。
🏭 実践計算
📊 すでに分かっている値
| 項目 | 値 | 計算済み |
|---|---|---|
| 総平方和 ST | 28 | 前回の記事 |
| 群間平方和 SA | 24 | さっき計算 |
計算
Se = 28 − 24 = 4
🎉 あっという間! Se = 4
これが「温度とは関係のない、偶然のバラつき」です。
ケーキで言えば、スポンジ部分の重さが「4」だと分かりました!
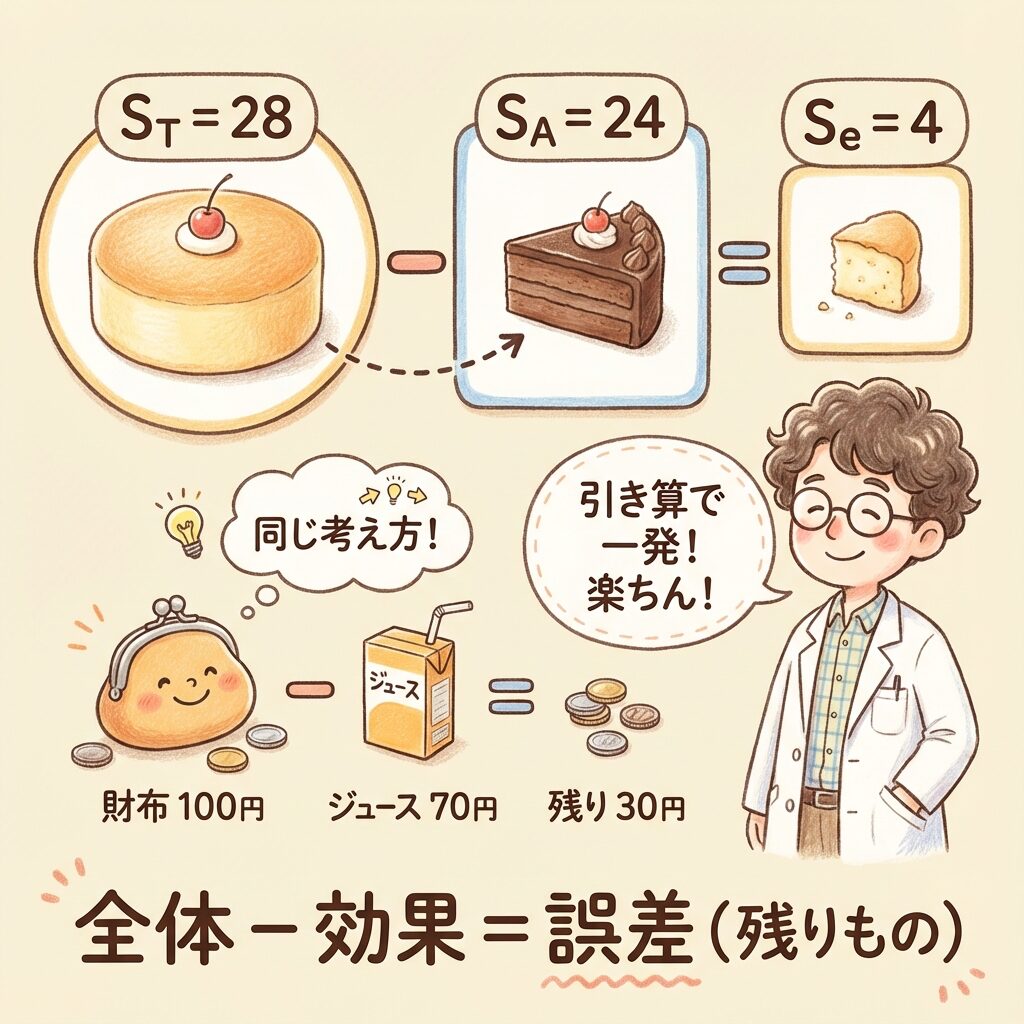
💡 なぜ引き算でOKなの?
ST = SA + Se という関係式が成り立つからです。
イメージ:財布に100円あって、ジュースに70円使ったら、残りは30円。
わざわざ小銭を数えなくても、引き算すれば分かりますよね。それと同じです!
4. 結果の解釈:シグナルとノイズ
計算結果を並べてみましょう。
📋 分解結果
| 成分 | 平方和(S) | 意味 | 割合 |
|---|---|---|---|
| 全体(ST) | 28 | 総エネルギー | 100% |
| 温度(SA) | 24 | シグナル(デカい!) | 86% |
| 誤差(Se) | 4 | ノイズ(小さい) | 14% |
📊 グラフで見ると一目瞭然
全体のバラつき(ST = 28)の内訳
バラつきの大部分(86%)は「温度の効果」によるもの!
どうでしょうか。
全体の「28」のうち、大部分の「24」は温度によるもので、誤差はたったの「4」しかありません。
この比率を見ただけでも、直感的に「あ、これは温度の影響がめちゃくちゃ強いな(実験成功だな)」と感じませんか?
🎯 直感的な解釈
✅ 効果 >> 誤差 の場合
「温度を変えたら、本当に強度が変わった!」
→ 実験成功
❌ 効果 ≒ 誤差 の場合
「温度を変えても、偶然のバラつきと区別がつかない…」
→ 効果があるとは言えない
この直感を、統計的に「合格!」と証明するのが、次のステップである「分散分析(ANOVA)」です。

まとめ
📝 今日のポイント
✅ 分解の公式
ST = SA + Se
全体 = 効果 + 誤差
✅ SA(群間平方和)
「各水準の合計の二乗」を使って計算
= 効果・シグナル
✅ Se(群内平方和)
引き算(ST − SA)で一発
= 誤差・ノイズ
これで、分散分析表を作るための「材料(S)」は全て揃いました。
📊 次回、これらを一枚の表にまとめ上げ、ついに「F値(シグナル ÷ ノイズ)」を算出します。
実験計画法のゴールまで、あと一歩です!
📖 次に読む記事
分散分析表(ANOVA)の作り方|表を完成させる手順|一元配置実験⑧
今回求めた平方和(S)を使って、いよいよ分散分析表を完成させます。S→V→Fの流れで、「効果があるか?」を統計的に判定できるようになります!
次の記事を読む →📚 あわせて読みたい
📖 一元配置実験マスター講座【全16回】
このシリーズを順番に読めば、一元配置実験を完全マスターできます!
