こんにちは、シラスです。
前回、回帰分析とは「未来を予測する数式を作る技術だ」とお話ししました。
しかし、統計学を学んでいると、よく似た言葉が出てきて混乱することがあります。
どちらも「2つのデータの関係性」を見る分析です。
Excelで散布図を描けば、見た目はほとんど同じです。
では、なぜわざわざ使い分ける必要があるのでしょうか?
「相関係数が高いなら、それで十分じゃないの?」
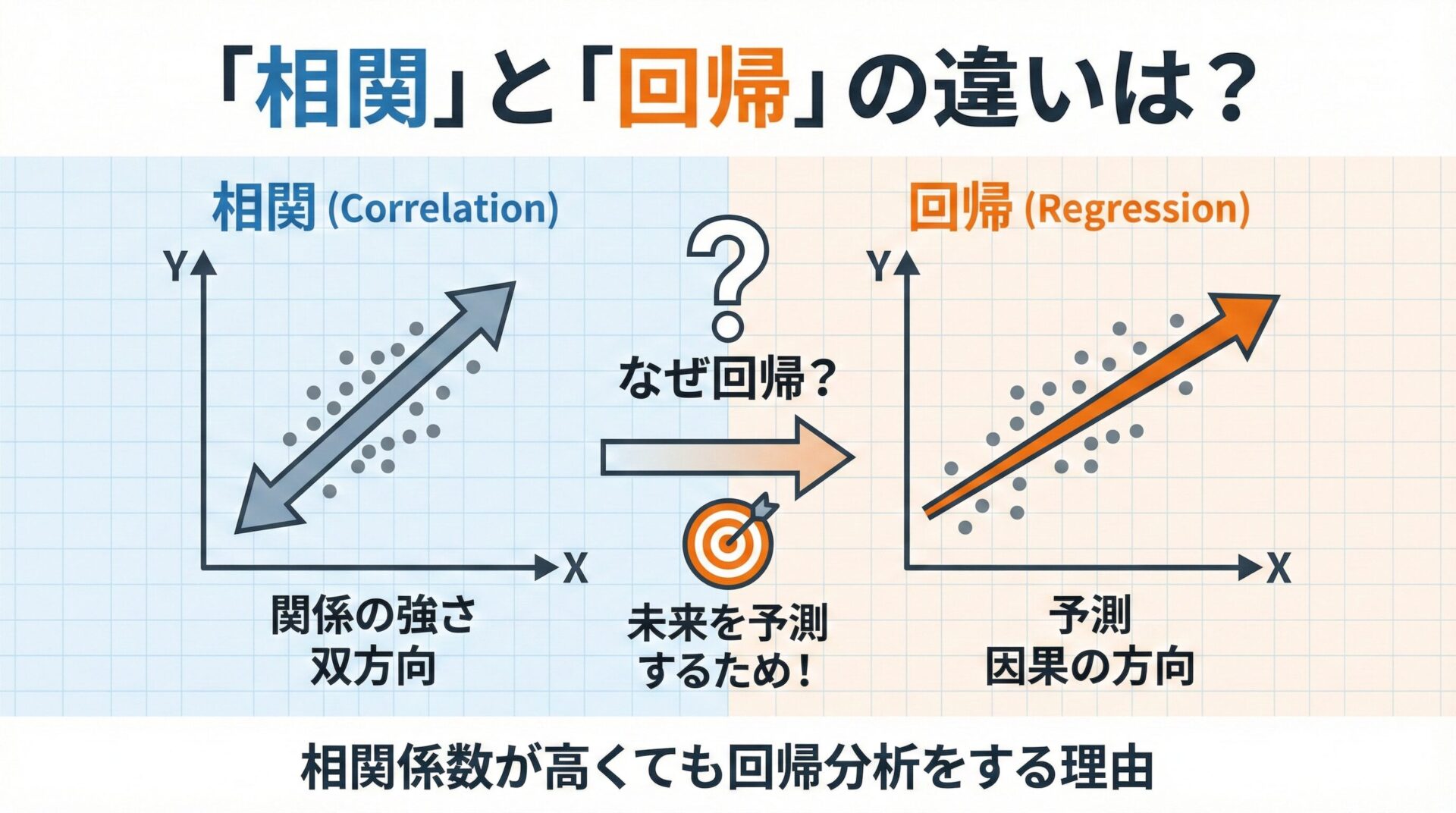
今日は、この2つの決定的な違いについて、「矢印の向き」という視点から解説します。
目次
1. 相関分析=「仲良し度」のチェック
まず、相関分析のイメージです。
これは「2つのデータがどれくらい連動しているか(仲が良いか)」を数値化するものです。
🤝 イメージ:恋人同士
「Aが笑えばBも笑う。Bが泣けばAも泣く」
お互いに関係し合っていますが、「どっちが主導権を握っているか(原因か)」は気にしません。
矢印は「双方向」です。
例えば、「身長」と「体重」には強い相関があります。
身長が高い人は体重も重い傾向にありますが、別に「身長が体重を操っている」わけでも「体重が身長を操っている」わけでもありません。
ただ単に「関係が深い($r=0.8$)」という事実があるだけです。
2. 回帰分析=「因果関係」のモデル化
一方、回帰分析はもっと踏み込みます。
「片方が原因で、もう片方が結果である」というストーリー(因果)を前提にします。
👨👦 イメージ:親と子
「親が決まれば、子の運命が決まる」
明確な上下関係があります。
$x$(説明変数)を動かすことで、$y$(目的変数)をコントロールしようとする試みです。
矢印は「一方通行」です。
例えば、「気温」と「おでんの売上」です。
気温が下がればおでんは売れますが、おでんをたくさん売っても気温は下がりませんよね?
この「一方的な影響力」を数式($y = ax + b$)にするのが回帰分析です。
3. 決定的違い:目的が違う
使い分けの基準はシンプルです。
あなたがデータ分析をして、最終的に何をしたいか?で選びます。
-
A. 現状を知りたい(診断)
→ 相関分析を使います。
「この変数はあっちの変数と関係がありそうだな」という探索段階。 -
B. 未来を知りたい(予測・制御)
→ 回帰分析を使います。
「広告費を10万円増やしたら、売上はいくら伸びる?」という具体的な数値予測。
相関係数がどれだけ高くても($0.99$とかでも)、それだけでは「広告費をいくらにすればいいか」は分かりません。
「アクション(行動)のための数式」を作るには、回帰分析が不可欠なのです。
まとめ
ビジネスの現場では、「関係があるね(相関)」で終わらせず、「だから、こうすれば数字はこう動くよ(回帰)」まで提示できて初めて価値が生まれます。
では、その「予測のための線(回帰直線)」は、具体的にどうやって引いているのでしょうか?
適当に定規で引いているわけではありません。
次回は、回帰分析の心臓部である計算ロジック、「最小二乗法(さいしょうにじょうほう)」の仕組みについて、バネの力に例えて解説します。
📚 回帰分析を「武器」にする3冊
数式アレルギーだった私でも読破できた、厳選の良書です。