こんにちは、シラスです。
前回、最小二乗法を使って、データの中に「最適な一本の線（回帰直線）」を引く方法を解説しました。
この直線の正体は、中学校で習った一次関数の方程式そのものです。
「ああ、懐かしいな。傾きと切片だっけ？」
そう思ったあなた、正解です。
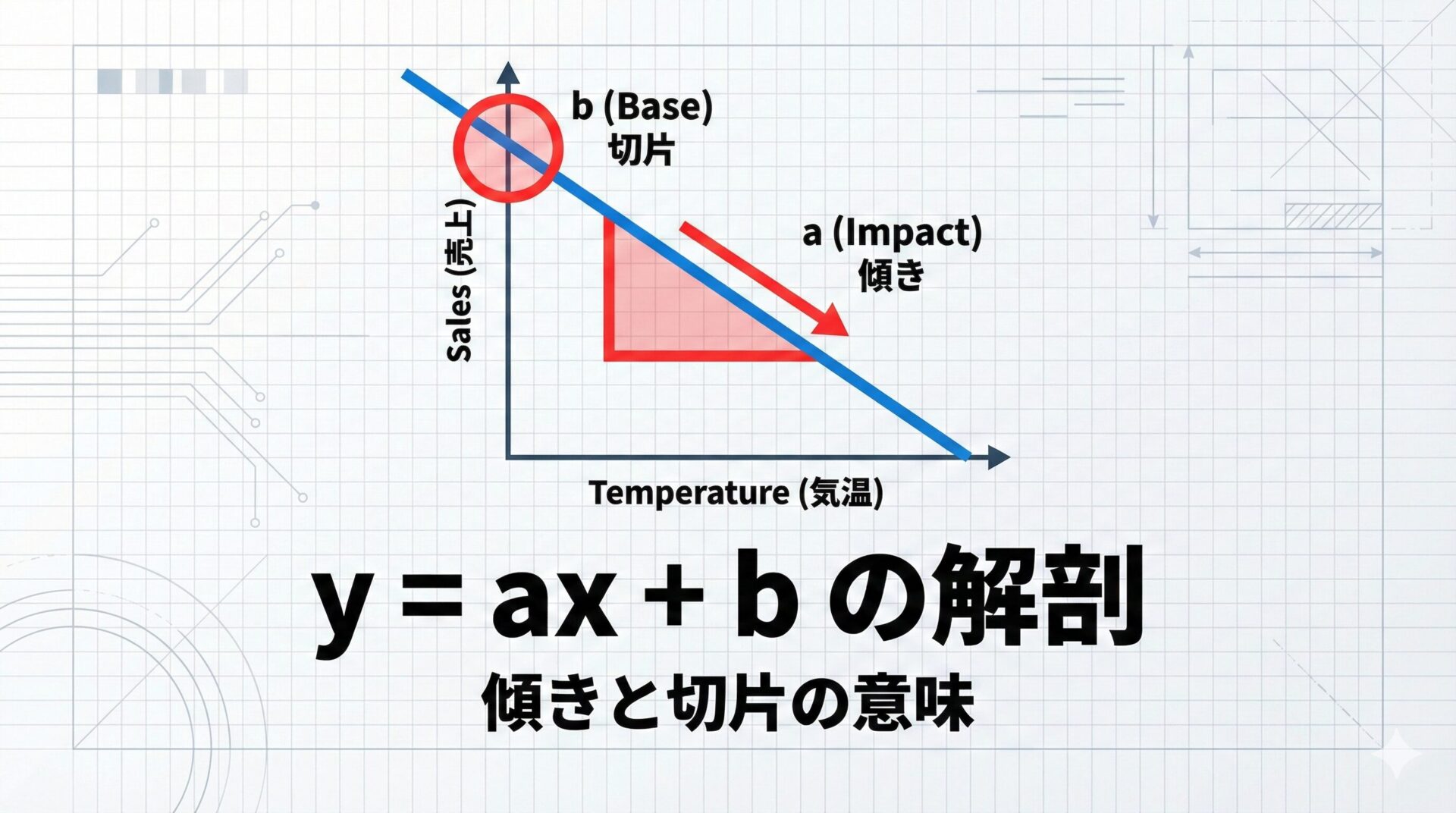
しかし、データ分析の現場において、この $a$（傾き）と $b$（切片）は単なる記号ではありません。
これらは、ビジネスや実験の結果を左右する「影響力」と「基礎体力」を表す、極めて重要なパラメータなのです。
今日は、このシンプルな数式の中に隠された「深い意味」を解剖していきます。
1. 式の正体：おでん屋で考える
イメージしやすいように、「気温（$x$）」から「おでんの売上（$y$）」を予測するモデルで考えてみましょう。
回帰分析の結果、以下の式が得られたとします。
この式を分解して、ビジネス的な意味を読み解いていきます。
2. 傾き $a$（回帰係数）＝「影響力の強さ」
まずは $x$ の前についている数字、$-10$（傾き）です。
統計学ではこれを「回帰係数（かいきけいすう）」と呼びます。
意味：「1変わると、どうなるか？」
傾きが $-10$ ということは、
「気温($x$)が 1℃ 上がると、売上($y$)は 10個 減る」
ということを表しています。
1℃上がっただけで、売上が50個も激減します。
つまり、この店は「気温の影響をものすごく受けやすい（敏感な）店」だということです。
逆に、傾きが「0」に近ければ、「気温が変わっても売上は変わらない（無関係）」という意味になります。
この数字を見るだけで、その要因（$x$）がどれくらい結果（$y$）を支配しているかが一発で分かるのです。
3. 切片 $b$（定数項）＝「ベースライン」
次に、後ろについている数字、$+300$（切片）です。
意味：「何もしなくてもあるもの」
切片とは、数学的には「$x=0$ の時の $y$ の値」です。
つまり、「気温が0℃の時の売上（基準値）」を表しています。
（※おでんの例だと0℃は極寒ですが、広告費の例なら「広告0円の時の自然売上」と考えると分かりやすいです）
切片が大きいということは、「基礎体力（ベースライン）」が高いということです。
要因($x$)に頼らなくても、ある程度の結果($y$)が出せる状態を示しています。
4. まとめ：ビジネスでの読み方
ここが大きい要因を見つけて対策すれば、結果を大きく変えられる（レバレッジが効く）。
ここが大きいと、環境変化に左右されにくい安定した状態と言える。
回帰分析の結果が出たら、ただ「予測できた！」と喜ぶだけでなく、この2つの数字をじっくり眺めてみてください。
「うちの店は傾きが大きすぎるな…もっと天候に左右されない商品（切片を上げる施策）が必要かも」
そんな深い経営戦略が見えてくるはずです。
さて、式はできました。
でも、この式で予測した値は、本当に当たるのでしょうか？
「計算はできたけど、実際のデータと全然合ってない（使い物にならない）」なんてこともあり得ます。
次回は、この予測式の精度（信頼度）を採点する指標、「決定係数（$R^2$）」について解説します。
📚 次に読むべき記事
相関と回帰の「違い」がわかったら、次は中身に進みましょう。今のあなたの状態に近いところから読むのがおすすめです。
🗺️ 迷ったらまずコレ🔍 STEP1：まずは「相関」をもっと深く
📈 STEP2：単回帰の「中身」を理解する
🚀 STEP3：実務レベルへ進む
💡 おすすめの進み方：まず STEP1 の3本で「相関」を固め、STEP2 で単回帰の中身を理解し、余力があれば STEP3 へ。順番に迷ったら、いつでも上のロードマップに戻ってきてください。