✅ この記事を読めば、「水タンク」と「水路」の例えで、直列・並列の公式が一生忘れられなくなります!
【電験三種・理論】コンデンサの直列・並列接続|合成容量の計算を完全マスター
こんにちは!電験三種の「理論」科目で、多くの受験生がつまずくのがコンデンサの直列・並列接続です。
特に、「直列は逆数の和、並列は単純な和」という公式の違いが、試験本番で混乱を招きます。公式を丸暗記しても、少し問題をひねられると「あれ?どっちだっけ?」となってしまうんですよね。
でも安心してください!この記事では、視覚的なイメージと身近な例え話を使って、公式の「本質」をゼロから徹底解説します。
結論から言うと、直列は「容量が小さくなる」、並列は「容量が大きくなる」という本質さえ理解すれば、もう公式を間違えることはありません。
📌 この記事のゴール
- 直列と並列の「合成容量の公式」を理解する
- なぜ直列は「逆数の和」なのかを説明できるようになる
- 試験で絶対に間違えない「見分け方」を身につける
- 混合回路(直列+並列)もスラスラ解けるようになる
目次
⚡ コンデンサとは?「電気を貯める素子」の正体
本題に入る前に、コンデンサ(キャパシタ)の基本をサクッと確認しましょう。「もう知ってるよ!」という方も、復習のつもりで読んでみてください。
コンデンサは、電気を「貯めたり」「放出したり」できる素子です。抵抗が「電流を妨げる」のに対して、コンデンサは「電気エネルギーを一時的に蓄える」という役割を持っています。
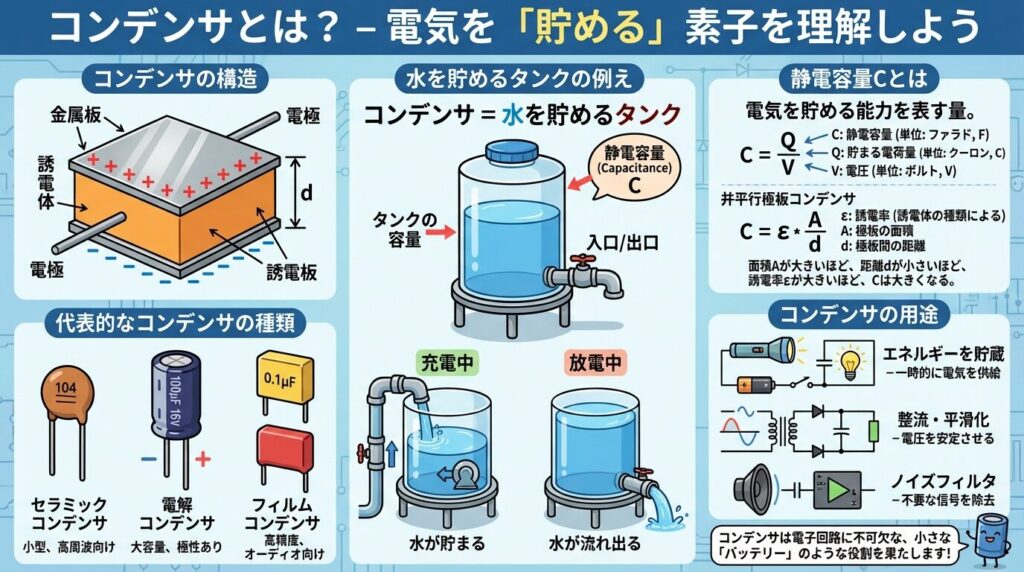
📦 コンデンサ = 水を貯める「タンク」
コンデンサを理解する一番簡単な方法は、「水タンク」に例えることです。これが直列・並列の理解にも直結するので、しっかりイメージしてください!
💧 水タンクの例え
・タンクの大きさ → コンデンサの静電容量C (単位: F ファラド)
・貯められる水の量 → 電気量Q (単位: C クーロン)
・水圧(高さ) → 電圧V (単位: V ボルト)
この関係を式で表すと、以下のようになります。
C = Q / V
つまり、「電圧1Vあたりに蓄えられる電気量」が静電容量Cの定義です。大きいタンクほどたくさん水を貯められるように、大きい容量のコンデンサほどたくさん電気を貯められるわけですね。
🔑 ポイント
コンデンサを「水タンク」とイメージすると、後の直列・並列の説明がスッと理解できます!この例えは試験本番でも使えるので、頭にしっかり刻んでおきましょう。
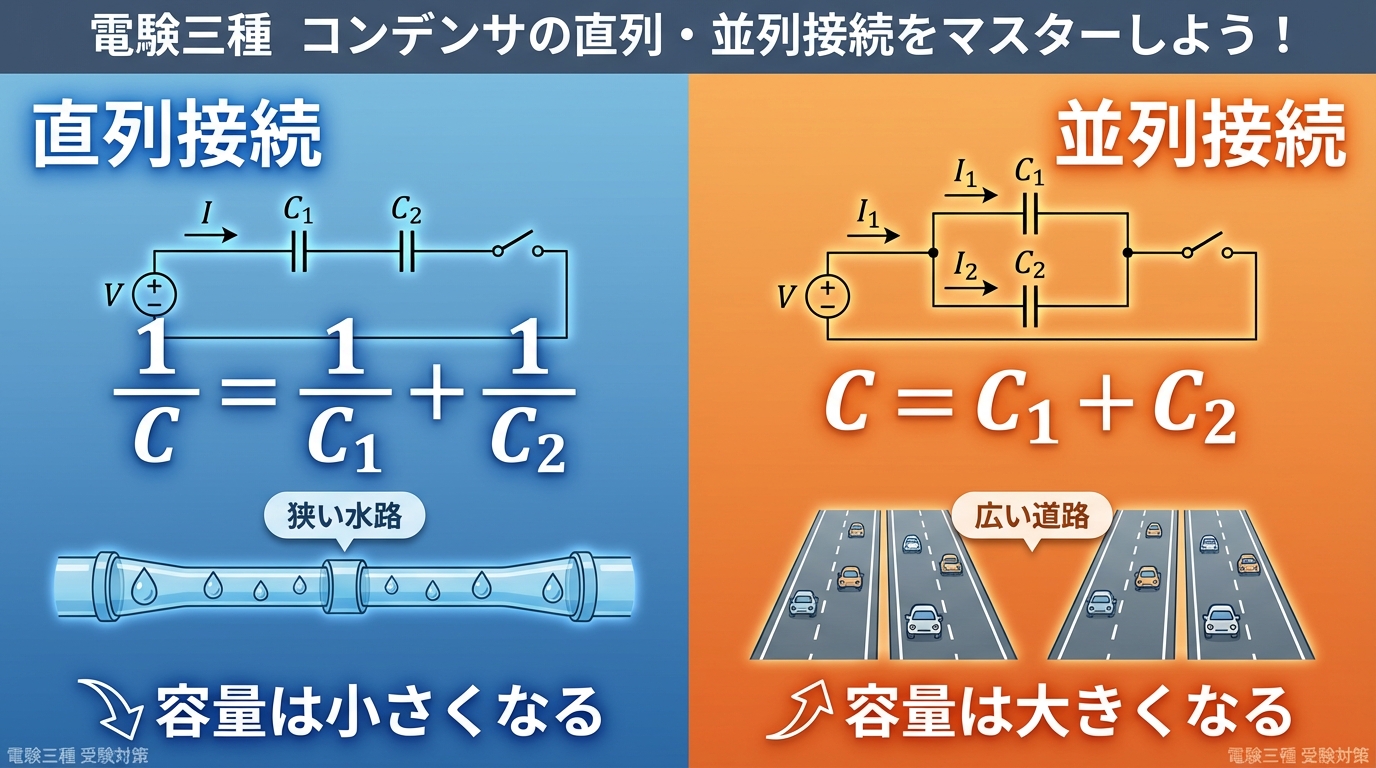
🔗 コンデンサの直列接続|なぜ「逆数の和」?
ここからが本題です!まずは直列接続から攻略しましょう。
直列接続は、抵抗の直列と同じく「一列に並べる」接続方法です。でも、抵抗とは違って容量が小さくなるという特徴があります。ここがポイントです!
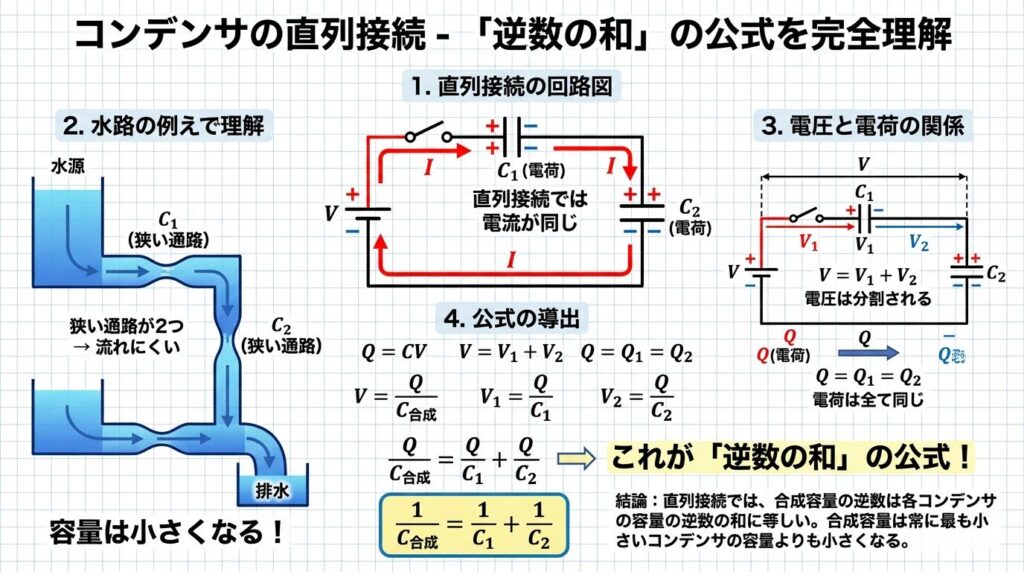
🌊 直列接続 = 「狭い水路」を2つ繋ぐイメージ
コンデンサを直列に繋ぐと、合成容量は必ず小さくなります。これは直感に反するかもしれませんが、水路の例えで考えると納得できます。
💧 水路の例え
細い水路を2つ直列に繋ぐと…
→ 全体として流れにくくなる = 容量が減る!
これと同じで、コンデンサも直列にすると「電気が貯まりにくく」なります。それぞれのコンデンサが「電圧を分担」するため、全体としての蓄電能力が下がるんです。
📐 直列接続の公式
「逆数の和」という、一見ややこしい形ですよね。でも、これには明確な理由があります。順を追って見ていきましょう。
🧮 なぜ逆数の和?公式の導出
直列接続では、各コンデンサに同じ電気量Qが蓄えられます。そして、電圧は分担されます。
Step 1: 各コンデンサの電圧
V₁ = Q/C₁, V₂ = Q/C₂
Step 2: 全体の電圧は足し算
V = V₁ + V₂
Step 3: 合成容量の定義
V = Q/C
Step 4: 代入して整理
Q/C = Q/C₁ + Q/C₂
Step 5: Qで割る
1/C = 1/C₁ + 1/C₂
これで「逆数の和」の正体がわかりましたね。直列では電圧が分担されるため、自然と逆数の形になるんです。
💡 計算例で実感!
【問題】
C₁ = 6μF、C₂ = 3μF を直列接続したとき、合成容量Cは?
【解答】
1/C = 1/6 + 1/3
1/C = 1/6 + 2/6 = 3/6 = 1/2
C = 2μF
✅ 確認: 元の6μFと3μFより、2μFの方が小さいですね!これが直列の特徴です。
⚠️ よくある間違い
- ❌ 直列なのに C = C₁ + C₂ と足し算してしまう
- ❌ 逆数計算した後、逆数を戻し忘れる
- ❌ 分数の計算でミスをする(通分を忘れる)
💡 覚え方: 「直列は『逆数』、抵抗と同じ!」
🌐 コンデンサの並列接続|シンプルな「足し算」!
続いて、並列接続を見ていきましょう。こちらは直列よりずっと簡単です!
並列接続は、複数のコンデンサを「横に並べる」接続方法です。この場合、容量が大きくなるのが特徴です。
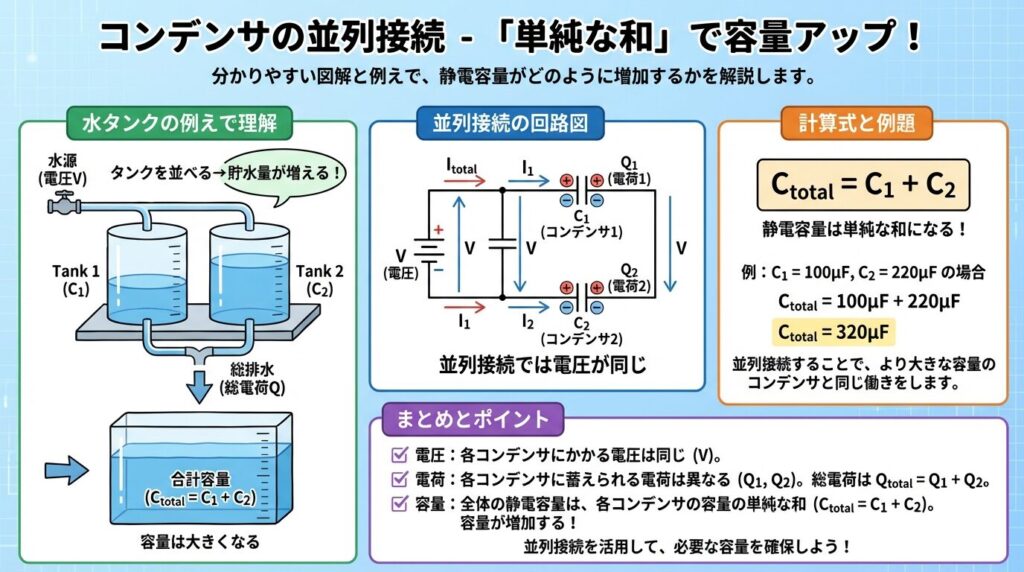
💧 並列接続 = 「水タンクを並べる」イメージ
コンデンサを並列に繋ぐと、合成容量は大きくなります。これは直感的にもわかりやすいですよね。
💧 水タンクの例え
大きいタンクを2つ並べると…
→ 貯水量が増える = 容量が増える!
これと同じで、コンデンサも並列にすると「たくさん電気が貯められる」ようになります。それぞれのコンデンサが「電気量を分担」するため、全体としての蓄電能力が上がるんです。
📐 並列接続の公式
シンプルな「足し算」です!逆数なんて出てきません。直列と比べると驚くほど簡単ですよね。
🧮 なぜ単純な和?公式の導出
並列接続では、各コンデンサに同じ電圧Vがかかります。そして、電気量は分担されます。
Step 1: 各コンデンサの電気量
Q₁ = C₁V, Q₂ = C₂V
Step 2: 全体の電気量は足し算
Q = Q₁ + Q₂
Step 3: 合成容量の定義
Q = CV
Step 4: 代入して整理
CV = C₁V + C₂V
Step 5: Vで割る
C = C₁ + C₂
並列では電気量が分担されるため、自然と「足し算」の形になります。直列とは逆のパターンですね!
💡 計算例で実感!
【問題】
C₁ = 4μF、C₂ = 6μF を並列接続したとき、合成容量Cは?
【解答】
C = C₁ + C₂
C = 4 + 6
C = 10μF
✅ 確認: 元の4μFと6μFより、10μFの方が大きいですね!これが並列の特徴です。
🎯 並列接続のポイント
- ✅ 公式が直列より簡単
- ✅ 単位をμFで揃える
- ✅ 必ず元より大きくなる
⚖️ 直列vs並列|絶対に間違えない見分け方
試験で最も重要なのは、「これは直列?並列?」を瞬時に判断することです。
📊 比較表で一発理解!
| 項目 | 直列接続 | 並列接続 |
|---|---|---|
| 回路図 | C₁ → C₂ (一列に並ぶ) | C₁と C₂ (横に並ぶ) |
| 合成容量の公式 | 1/C = 1/C₁ + 1/C₂ | C = C₁ + C₂ |
| 容量の変化 | 小さくなる ↓ | 大きくなる ↑ |
| 例え | 狭い水路を繋ぐ | 水タンクを並べる |
| 同じ値 | 電気量Q | 電圧V |
| 抵抗との関係 | 抵抗の直列と同じ | 抵抗の並列と逆 |
💡 覚え方のコツ
- 直列 = 「逆数の和」、抵抗と同じ
- 並列 = 「単純な和」、抵抗と逆
- 直列は狭い水路(流れにくい)、並列は大きいタンク(たくさん貯まる)
🔍 回路図での見分け方
【直列接続の特徴】
✅ コンデンサが一列に並んでいる
✅ 電流が1つの道を通る
✅ 「数珠つなぎ」「電車の車両」のイメージ
【並列接続の特徴】
✅ コンデンサが横に並んでいる
✅ 電流が複数の道に分かれる
✅ 「高速道路の車線」「並んだタンク」のイメージ
🔢 3つ以上のコンデンサを接続する場合
実際の試験では、3つ以上のコンデンサが出題されることもあります。でも、考え方は同じです!
📐 直列の場合
公式:
1/C = 1/C₁ + 1/C₂ + 1/C₃ + ...
計算例: C₁ = C₂ = C₃ = 9μF のとき
1/C = 1/9 + 1/9 + 1/9 = 3/9 = 1/3
C = 3μF
✅ 同じ容量のコンデンサをn個直列にすると、C = C₁/nになります!
📐 並列の場合
公式:
C = C₁ + C₂ + C₃ + ...
計算例: C₁ = 2μF、C₂ = 3μF、C₃ = 5μF のとき
C = 2 + 3 + 5
C = 10μF
✅ どんどん足すだけ!超簡単です。
🎯 試験テクニック
同じ容量のコンデンサが複数ある場合、パターンを覚えておくと計算が速くなります!
・直列n個 → C = C₁/n
・並列n個 → C = n×C₁
🎯 混合回路の解き方|直列+並列が混在する問題
試験では、直列と並列が混在した「混合回路」が頻出です。落ち着いて、順番に計算しましょう!
🔧 解法の3ステップ
Step 1: 回路図を見て、構造を把握
→ どこが直列で、どこが並列かを見極める
Step 2: 内側から順番に計算
→ 並列部分を先に計算 → 次に直列部分を計算
Step 3: 最終的な合成容量を求める
→ 段階的に簡略化していく
💡 練習問題
【問題】
C₁ = 6μF と C₂ = 3μF が並列、その結果が C₃ = 9μF と直列になっている。合成容量Cは?
【解答】
Step 1: C₁とC₂の並列部分を計算
C₁₂ = C₁ + C₂ = 6 + 3 = 9μF
Step 2: C₁₂とC₃の直列を計算
1/C = 1/C₁₂ + 1/C₃
1/C = 1/9 + 1/9 = 2/9
C = 4.5μF
✅ ポイント
混合回路は「内側から外側へ」順番に計算するのがコツ!
焦らず、一つずつ確実に進めましょう。
📚 電験三種での出題パターンと対策
最後に、電験三種の試験対策を確認しましょう。この単元は毎年のように出題されます!
📝 頻出パターン3選
【パターン1】 単純な直列または並列の計算
→ 公式を覚えていれば30秒で解ける!
【パターン2】 混合回路の合成容量
→ 内側から順に計算。焦らず段階的に。
【パターン3】 電気量Qや電圧Vを求める問題
→ 合成容量を求めた後、Q=CVを使う。
⚠️ よくあるミス
- ❌ 直列と並列の公式を逆に覚えている
- ❌ 逆数計算後、最後に逆数を戻し忘れる
- ❌ 単位がμFとpFで混在していることに気づかない
- ❌ 混合回路で、計算の順番を間違える
🎓 合格への学習法
1. 公式を「イメージ」で覚える
→ 水タンク、水路の例えを頭に思い浮かべる
2. 抵抗との関係を理解する
→ 直列は抵抗と同じ、並列は逆
3. 過去問を最低10問解く
→ 出題パターンは限られているので、慣れれば確実に得点できます!
4. 計算ミスを減らす工夫
→ 「合成容量が元より大きいか小さいか」で検算する習慣をつける
🏆 まとめ
✅ 直列接続 = 「逆数の和」、容量は小さくなる
→ 1/C = 1/C₁ + 1/C₂
✅ 並列接続 = 「単純な和」、容量は大きくなる
→ C = C₁ + C₂
✅ 覚え方 = 直列は「狭い水路」、並列は「大きいタンク」
✅ 混合回路 = 内側から順番に計算
✅ 試験対策 = 過去問で計算スピードを上げる
🔗 関連記事で理解を深めよう!
この記事を読んだあなたは、もうコンデンサの直列・並列接続で迷うことはありません。
試験本番で自信を持って解答できるよう、しっかり練習しておきましょう!
電験三種合格、応援しています!🎓