😰 こんな悩みはありませんか?
- 変圧器の公式が多すぎて覚えられない…
- 巻数比「a」って何?どう使うの?
- 電圧比と電流比、どっちがどっちか混乱する
- インピーダンス比の「a²」が意味不明…
変圧器の計算問題を解こうとすると、公式がたくさん出てきて混乱しますよね。
でも、安心してください。実は変圧器の公式はたった1つの「a」を理解するだけで、すべてが芋づる式に出てくるのです。
✅ この記事の結論
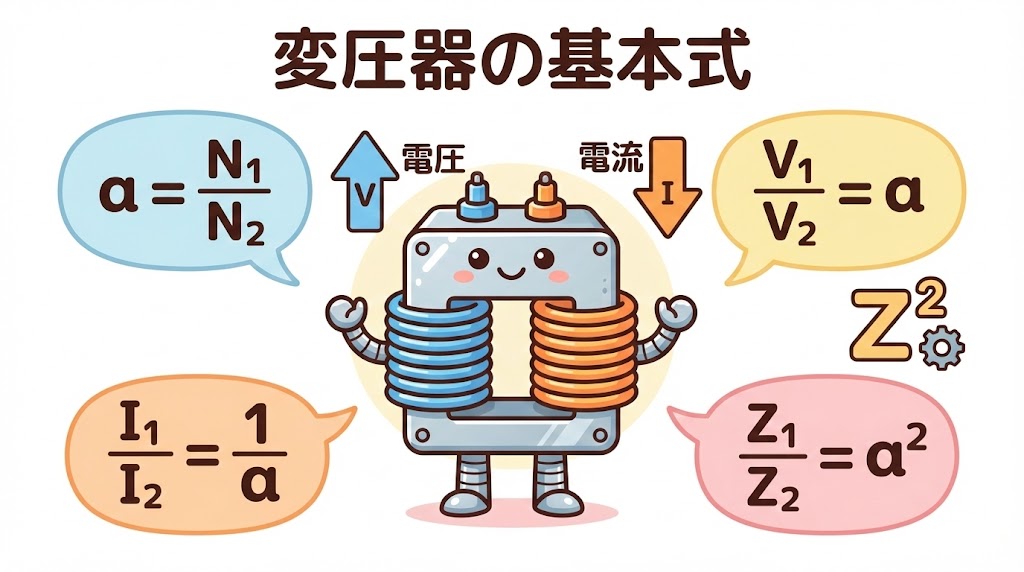
変圧器の計算は「巻数比 a」がすべての基準。
電圧は「a倍」、電流は「1/a倍」、インピーダンスは「a²倍」。
この3つの関係を覚えれば、どんな問題も解ける!
この記事では、変圧器の4つの基本式を「なぜそうなるのか?」から丁寧に解説します。
読み終わる頃には、「aさえわかれば全部計算できる!」という自信がつきますよ。
目次
🔢 巻数比「a」とは? ― すべての計算の出発点
変圧器の計算で最初に覚えるべきは、「巻数比 a(エー)」です。
これは、一次コイルと二次コイルの巻数の「比率」を表す数字です。
a = N₁ / N₂
N₁:一次コイルの巻数 | N₂:二次コイルの巻数 | a:巻数比
この「a」という文字が、変圧器の計算における絶対的な基準になります。
💡 巻数比aの意味を具体例で理解しよう
例えば、一次コイルが1000回、二次コイルが100回の変圧器があったとします。
📝 計算例
a = N₁ / N₂ = 1000 / 100 = 10
この場合、巻数比 a = 10 です。
「一次コイルは二次コイルの10倍の巻数がある」という意味ですね。
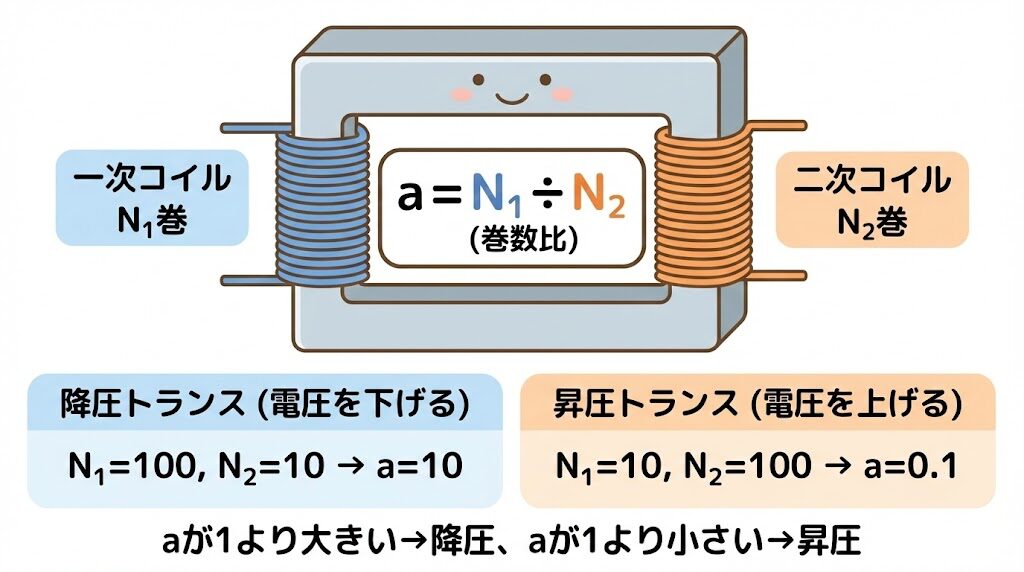
💡 aの値で変圧器のタイプがわかる!
・a > 1(1より大きい)→ 降圧トランス(電圧を下げる)
・a < 1(1より小さい)→ 昇圧トランス(電圧を上げる)
・a = 1 → 電圧は変わらない(絶縁用など)
⚡ 電圧比 = 巻数比a
巻数比aがわかったら、次は電圧比です。
これは前回の記事でも説明しましたが、もう一度確認しましょう。
V₁ / V₂ = N₁ / N₂ = a
V₁:一次電圧 | V₂:二次電圧
つまり、電圧比は巻数比と同じです。
これを式変形すると、二次電圧を求める公式が出てきます。
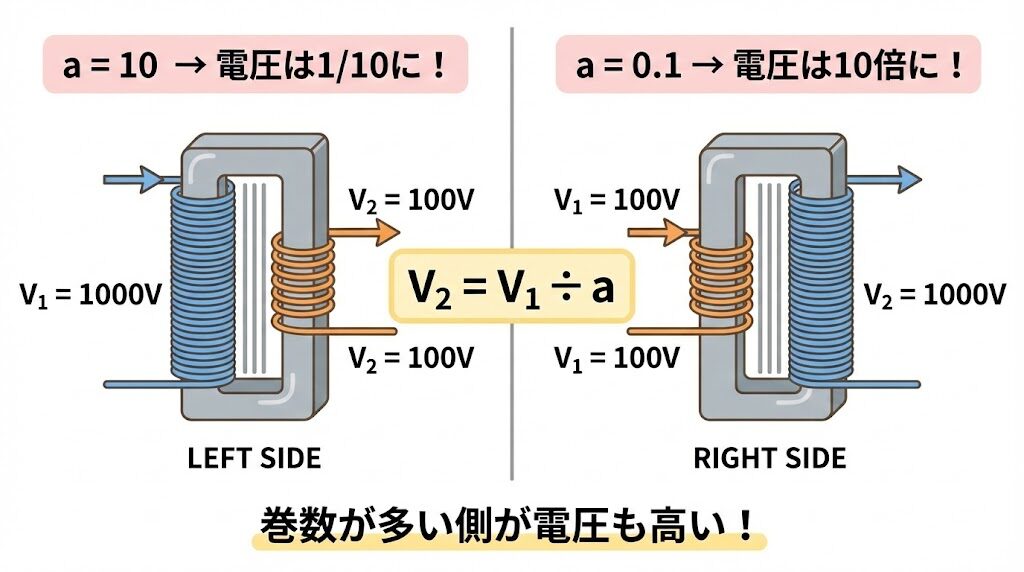
V₂ = V₁ / a
一次電圧を巻数比で割れば、二次電圧が求まる
🧮 電圧比の計算例
📝 例題
【条件】
・一次電圧 V₁ = 6,600V
・巻数比 a = 33
【計算】
V₂ = V₁ / a = 6,600 / 33 = 200V
【答え】 二次電圧は200V
6,600Vが200Vに降圧されました。これは電柱の変圧器でよく見る変換ですね。
✅ 電圧比のポイント
・電圧比 = 巻数比 = a
・巻数が多い側が、電圧も高い
・V₂ = V₁ / a で二次電圧を計算
🔄 電流比 = 巻数比の「逆」(1/a)
電圧の次は電流です。ここで超重要なポイントがあります。
電流比は、電圧比の「逆」になる!
I₁ / I₂ = N₂ / N₁ = 1/a
I₁:一次電流 | I₂:二次電流
なぜ逆になるのでしょうか?
それは、エネルギー(電力)が保存されるからです。
⚖️ なぜ電流比は逆になる? ― 電力保存の法則
理想変圧器では、入力電力と出力電力が等しくなります。
V₁ × I₁ = V₂ × I₂
一次側の電力 = 二次側の電力(理想変圧器の場合)
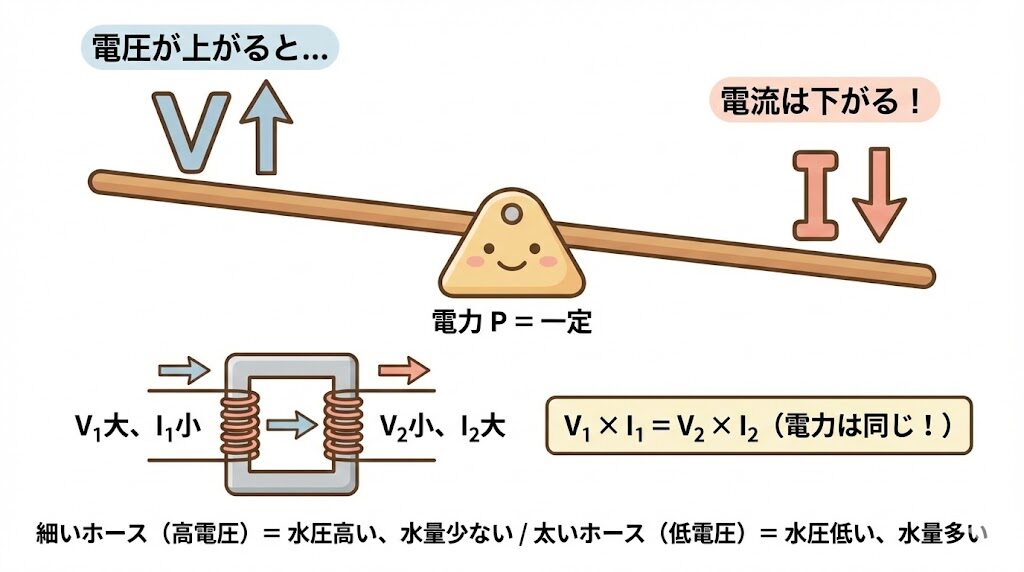
この式を見ると、電圧と電流はシーソーの関係にあることがわかります。
🎢 シーソーで考える
シーソーの左右のバランスは常に保たれます。
・電圧が上がると → 電流は下がる
・電圧が下がると → 電流は上がる
トータルの「重さ」(電力)は変わらないのです。
🧮 電流比の計算例
📝 例題
【条件】
・一次電流 I₁ = 1A
・巻数比 a = 10
【計算】
I₂ = I₁ × a = 1 × 10 = 10A
【答え】 二次電流は10A
電圧が1/10になったので、電流は10倍になりました。
電力は「10 × 1 = 10」のままで変わりません。
I₂ = I₁ × a
一次電流に巻数比をかければ、二次電流が求まる
✅ 電流比のポイント
・電流比 = 巻数比の逆 = 1/a
・巻数が少ない側が、電流は多い
・I₂ = I₁ × a で二次電流を計算
🔷 インピーダンス比 = 巻数比の「2乗」(a²)
最後に登場するのがインピーダンス比です。
これは少し難しく見えますが、「電圧」と「電流」の関係から自然に導けます。
Z₁ / Z₂ = (N₁/N₂)² = a²
Z₁:一次側に換算したインピーダンス | Z₂:二次側のインピーダンス
なぜ「2乗」になるのでしょうか?

🔍 なぜ「a²」になる? ― オームの法則から導く
インピーダンスZは、オームの法則から「Z = V / I」で表されます。
これを使って、インピーダンス比を計算してみましょう。
📝 インピーダンス比の導出
【ステップ1】 インピーダンスの定義
Z₁ = V₁ / I₁ 、 Z₂ = V₂ / I₂
【ステップ2】 比を取る
Z₁ / Z₂ = (V₁/I₁) / (V₂/I₂)
【ステップ3】 式を変形
Z₁ / Z₂ = (V₁/V₂) × (I₂/I₁)
【ステップ4】 電圧比と電流比を代入
Z₁ / Z₂ = a × a = a²
電圧比が「a」で、電流比が「1/a」なので、インピーダンス比は「a × a = a²」になるのです。
🔎 イメージで覚える
「a²」は、aの効果が2回かかるということ。
・1回目:電圧がa倍になる効果
・2回目:電流が1/a倍(÷aになる)効果
この2つが掛け合わさって「a × a = a²」になります。
🧮 インピーダンス比の計算例
📝 例題:二次側のインピーダンスを一次側に換算
【条件】
・二次側に接続された負荷 Z₂ = 4Ω
・巻数比 a = 5
【計算】
Z₁ = Z₂ × a² = 4 × 5² = 4 × 25 = 100Ω
【答え】 一次側から見たインピーダンスは100Ω
二次側の4Ωの負荷が、一次側から見ると100Ωに見えるということです。
これを「インピーダンス変換」または「一次側換算」と呼びます。
✅ インピーダンス比のポイント
・インピーダンス比 = 巻数比の2乗 = a²
・Z₁ = Z₂ × a² で一次側換算
・Z₂ = Z₁ / a² で二次側換算
・「a²」は電圧と電流の両方の効果
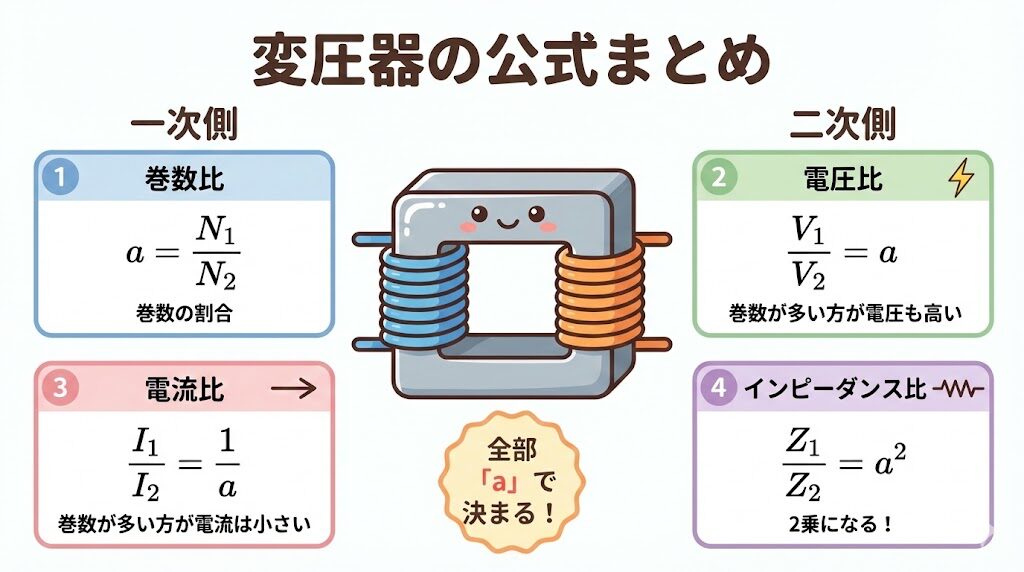
📊 変圧器の基本式まとめ
ここまで学んだ4つの公式を、一覧表にまとめます。
| 項目 | 公式 | 覚え方 |
|---|---|---|
| 巻数比 | a = N₁/N₂ | すべての基準 |
| 電圧比 | V₁/V₂ = a | そのまま「a」 |
| 電流比 | I₁/I₂ = 1/a | 電圧の逆 |
| インピーダンス比 | Z₁/Z₂ = a² | 電圧の2乗 |
| 電力 | P₁ = P₂ | 変わらない(理想時) |
🧠 暗記のコツ
「V は a、I は 1/a、Z は a²」
・電圧(Voltage)は巻数比そのまま
・電流(Current)は巻数比の逆数
・インピーダンス(Z)は巻数比の2乗
🎯 実践問題で確認しよう
最後に、実際の試験で出題されそうな問題を解いてみましょう。
📝 練習問題
【問題】
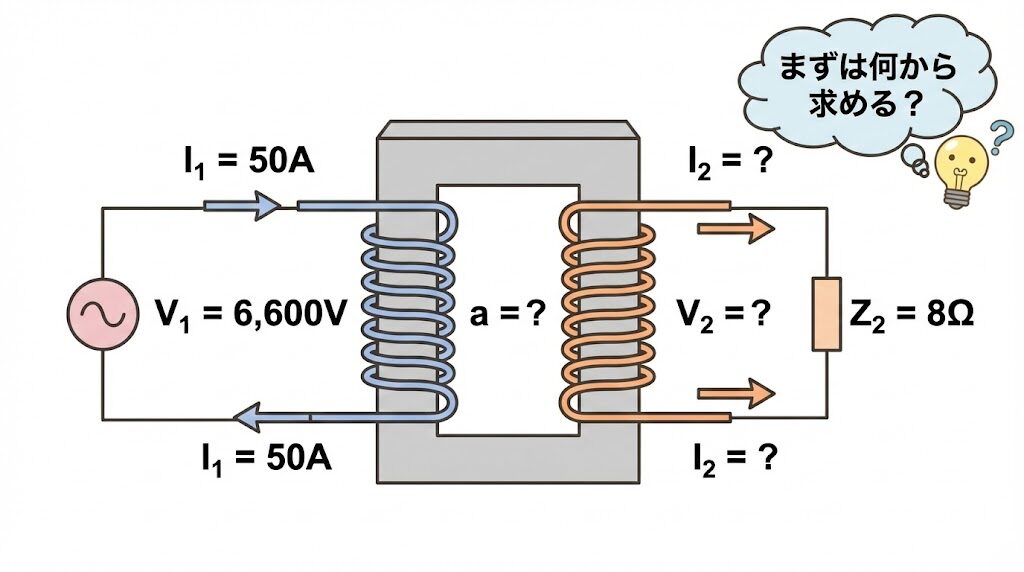
理想変圧器があり、一次側に6,600V、50Aの交流電源が接続されている。
二次側には8Ωの抵抗負荷が接続されている。
次の値を求めよ。
(1) 二次電圧 V₂
(2) 二次電流 I₂
(3) 巻数比 a
✅ 解答と解説
📝 解答
【考え方】
まず、一次側の情報から「一次側から見たインピーダンス Z₁」を求めます。
【ステップ1】一次側インピーダンスを求める
Z₁ = V₁ / I₁ = 6,600 / 50 = 132Ω
【ステップ2】巻数比aを求める
Z₁ / Z₂ = a² より
a² = Z₁ / Z₂ = 132 / 8 = 16.5
a = √16.5 ≒ 4.06
【ステップ3】二次電圧V₂を求める
V₂ = V₁ / a = 6,600 / 4.06 ≒ 1,626V
【ステップ4】二次電流I₂を求める
I₂ = I₁ × a = 50 × 4.06 ≒ 203A
または V₂ / Z₂ = 1,626 / 8 ≒ 203A でも同じ結果。
✅ 検算:電力は一致するか?
P₁ = V₁ × I₁ = 6,600 × 50 = 330,000W
P₂ = V₂ × I₂ = 1,626 × 203 ≒ 330,000W
ほぼ一致!理想変圧器なので、電力が保存されています。
📝 まとめ:変圧器の基本式
☕ 今日のおさらい
- 巻数比 a = N₁/N₂:すべての計算の出発点
- 電圧比 = a:巻数が多い方が電圧も高い
- 電流比 = 1/a:巻数が多い方が電流は小さい
- インピーダンス比 = a²:電圧と電流の両方の効果で2乗になる
- 電力は一定:V₁I₁ = V₂I₂(理想変圧器)
変圧器の計算問題は、「巻数比aを求める→他の値を芋づる式に計算」という流れが基本です。
今回の公式をしっかり覚えて、次の「等価回路」の学習に進みましょう!
💪
変圧器の基本式、マスターできましたか?
「aさえわかれば全部解ける!」を合言葉に、次へ進みましょう!