![Pinterest](https://www.pinterest.com/pin/create/button/?url=https%3A%2F%2Fshirasusolo.net%2Fstatistics%2Fregression-analysis%2Fpost-5209%2F&media=https://shirasusolo.net/wp-content/uploads/2026/01/BV6TQmPs.jpeg&description=😣 こんな悩みはありませんか？ 「平方和って何？SR、Se、STの違いがわからない…」 「分散分析表の数字、どうやって計算するの？」 「"バラつきを分解する"ってど){kind=link}
- 「平方和って何？SR、Se、STの違いがわからない…」
- 「分散分析表の数字、どうやって計算するの？」
- 「"バラつきを分解する"ってどういう意味？」
- 3つの平方和（SR, Se, ST）の意味をイメージで理解
- 「ST = SR + Se」の関係を図解
- 具体的な数値を使った計算手順
- 分散分析表を作る準備が完了
前回の記事で、正規方程式を使って偏回帰係数を求める方法を学びました。
でも、係数が求まっただけでは不十分です。次に知りたいのは、
「この重回帰式、本当に役に立っているの？」
ということですよね。
それを判断するために、まず「平方和の分解」を理解する必要があります。
この記事では、「平方和」とは何か、なぜ分解するのか、どうやって計算するのかを、具体例を使って徹底解説します。
【計算例あり】重回帰の正規方程式｜偏回帰係数と切片を求める全手順 →
🎯 平方和とは？
まず、「平方和」という言葉の意味を押さえましょう。
「偏差（平均からのズレ）を2乗して、すべて足し合わせたもの」です。
データのバラつきの大きさを表す指標です。
「平方」は「2乗」、「和」は「合計」という意味ですね。
偏差をそのまま足すと、プラスとマイナスが打ち消し合ってゼロになってしまうからです。2乗することで、すべてプラスになり、バラつきの大きさを正しく測れます。
第5回：分散と標準偏差｜「バラつき」を数値化する魔法の公式 →
🧩 3つの平方和の意味
重回帰分析では、3つの平方和を計算します。
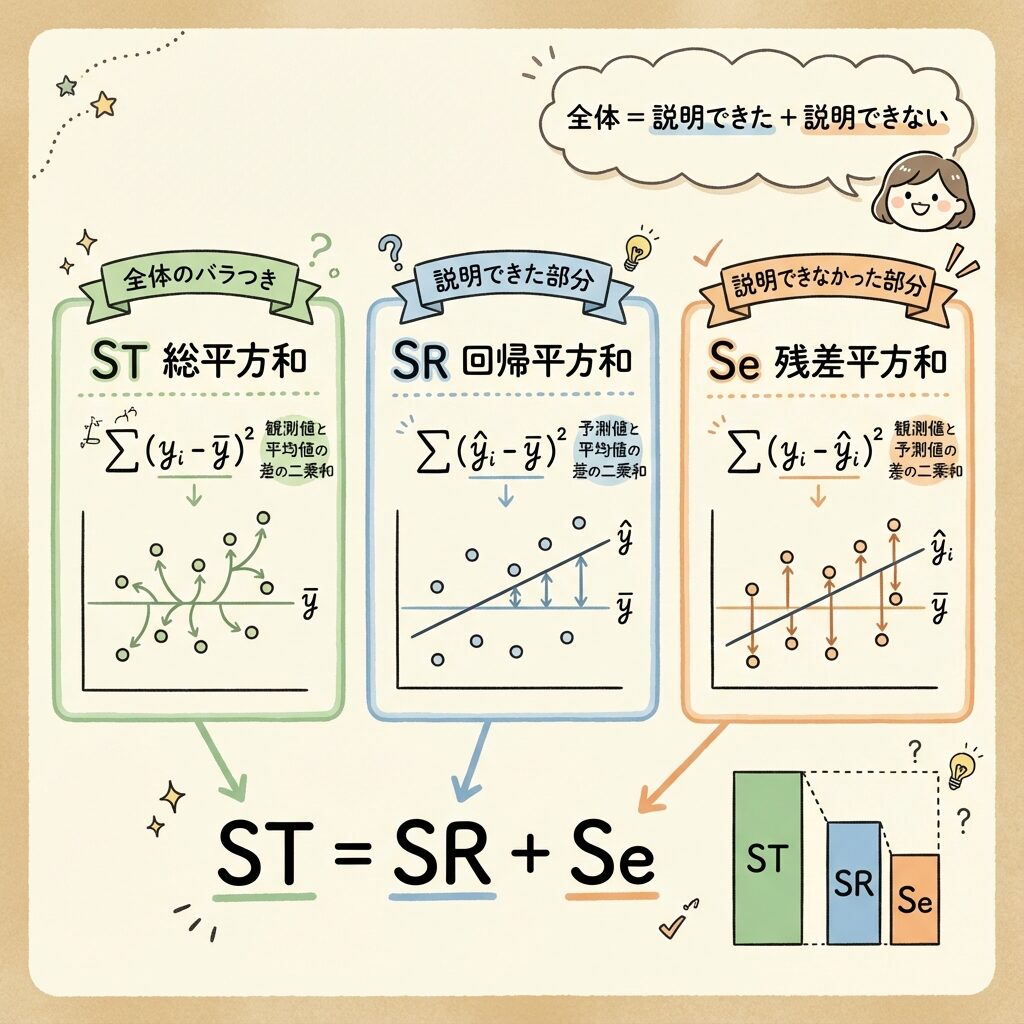
🟢 総平方和 ST（Total Sum of Squares）
意味：目的変数yの全体のバラつき
「各データが平均からどれだけ離れているか」の合計
これは「説明する前の、yのバラつき全体」を表しています。
🔵 回帰平方和 SR（Regression Sum of Squares）
意味：回帰式で説明できるバラつき
「予測値が平均からどれだけ離れているか」の合計
これは「重回帰式のおかげで説明できた部分」を表しています。SRが大きいほど、回帰式が役に立っています。
🟠 残差平方和 Se（Error Sum of Squares）
意味：回帰式で説明できないバラつき（残差）
「実測値と予測値のズレ」の合計
これは「重回帰式では説明しきれなかった誤差」を表しています。Seが小さいほど、回帰式の当てはまりが良いです。
【完全図解】残差と誤差の違い｜見えるズレと見えないズレを徹底解説 →
🍰 「バラつきの分解」をイメージで理解
3つの平方和の関係を、ケーキの分割でイメージしてみましょう。
🎂 ケーキの例え
【yのバラつき = 1つのホールケーキ】
|
🟢 ST
ホールケーキ全体 （全バラつき） |
= |
🔵 SR
食べた部分 （説明できた） |
+ |
🟠 Se
残った部分 （説明できない） |
つまり、yのバラつき全体（ST）を、「回帰で説明できた部分（SR）」と「説明できなかった部分（Se）」に分けるのです。
全体のバラつき = 説明できた + 説明できなかった
📊 グラフでイメージする
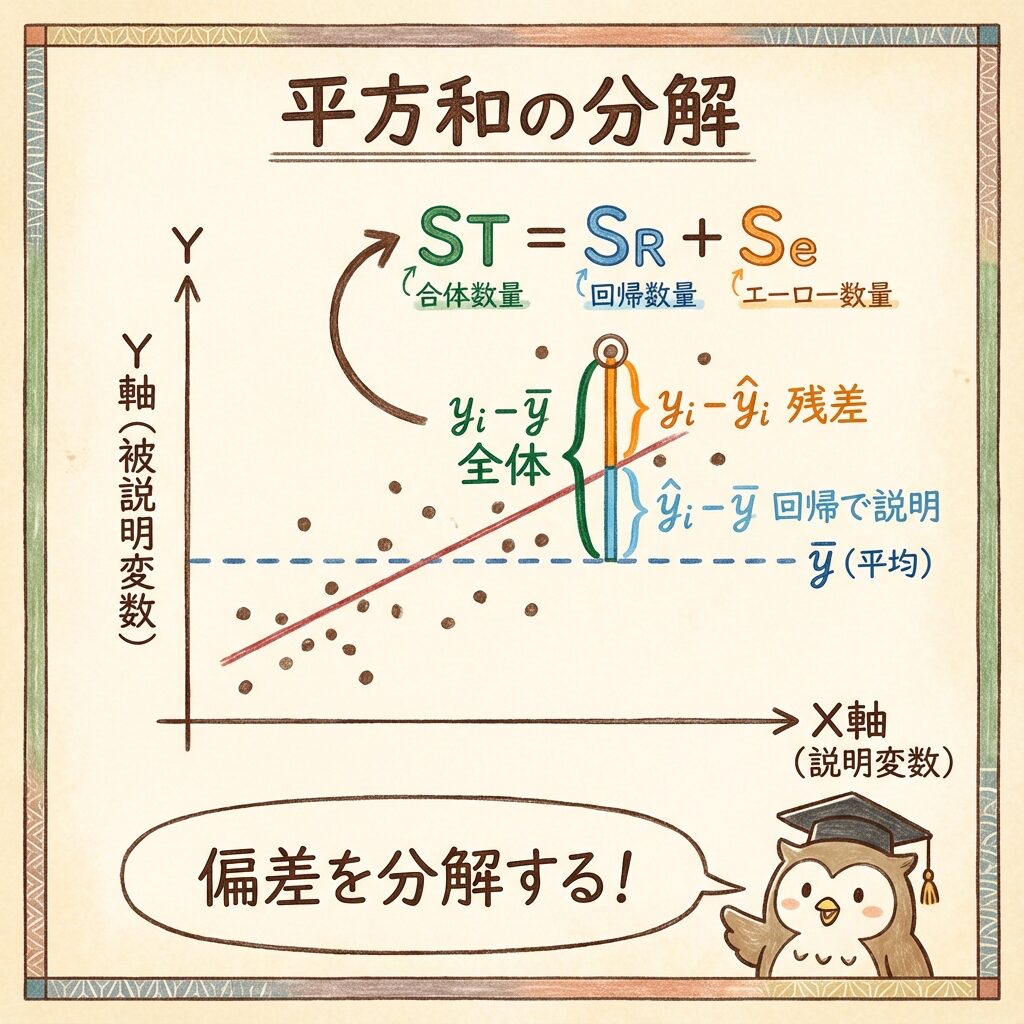
1つのデータ点について、平方和の分解を視覚的に見てみましょう。
（yᵢ − ȳ）= （ŷᵢ − ȳ）+ （yᵢ − ŷᵢ）
これを2乗して全データで合計すると、ST = SR + Se になります。
🎯 なぜ平方和を分解するの？
平方和を分解する目的は、「回帰式がどれだけ役に立っているか」を数値で評価するためです。
| 状況 | SRとSeの関係 | 意味 |
|---|---|---|
| 理想的 😊 | SR 大、Se 小 | 回帰式でほとんど説明できている |
| ダメ 😢 | SR 小、Se 大 | 回帰式が役に立っていない |
決定係数 R² = SR / ST です。つまり「全体のバラつきのうち、何%を回帰で説明できたか」を表します。
決定係数(R²)の正体｜「あてはまりの良さ」を視覚的に理解する →
📊 具体例で計算してみよう
前回の記事で使った「製品の強度」のデータで、実際に平方和を計算してみましょう。
📋 使用するデータ
前回求めた重回帰式：y = 2.4 + 1.53x₁ + 1.33x₂
| No. | x₁ | x₂ | 実測値 y | 予測値 ŷ |
|---|---|---|---|---|
| 1 | 1 | 1 | 5 | 5.27 |
| 2 | 2 | 1 | 7 | 6.80 |
| 3 | 3 | 2 | 10 | 9.67 |
| 4 | 4 | 2 | 11 | 11.20 |
| 5 | 5 | 3 | 14 | 14.07 |
| 平均 | ȳ = 9.4 | − | ||
yの平均は ȳ = (5+7+10+11+14)/5 = 9.4 です。
🟢 Step 1：総平方和 ST を計算
ST = Σ(yᵢ − ȳ)² を計算します。
| No. | y | y − ȳ | (y − ȳ)² |
|---|---|---|---|
| 1 | 5 | 5 − 9.4 = −4.4 | 19.36 |
| 2 | 7 | 7 − 9.4 = −2.4 | 5.76 |
| 3 | 10 | 10 − 9.4 = 0.6 | 0.36 |
| 4 | 11 | 11 − 9.4 = 1.6 | 2.56 |
| 5 | 14 | 14 − 9.4 = 4.6 | 21.16 |
| 合計 | ST = 49.20 | ||
🟠 Step 2：残差平方和 Se を計算
Se = Σ(yᵢ − ŷᵢ)² を計算します。
| No. | y | ŷ | y − ŷ（残差） | (y − ŷ)² |
|---|---|---|---|---|
| 1 | 5 | 5.27 | −0.27 | 0.07 |
| 2 | 7 | 6.80 | 0.20 | 0.04 |
| 3 | 10 | 9.67 | 0.33 | 0.11 |
| 4 | 11 | 11.20 | −0.20 | 0.04 |
| 5 | 14 | 14.07 | −0.07 | 0.00 |
| 合計 | Se = 0.27 | |||
🔵 Step 3：回帰平方和 SR を計算
SR は「ST − Se」で求めるのが簡単です。
SR = 49.20 − 0.27
SR = 48.93
SR = Σ(ŷᵢ − ȳ)² でも計算できますが、ST − Se の方が計算ミスが少なくおすすめです。
総平方和（St）の計算｜データ全体のバラつきを数値化する →
🎉 結果のまとめと解釈
📊 計算結果
| 平方和 | 値 | 割合 | 意味 |
|---|---|---|---|
| ST（総） | 49.20 | 100% | yの全バラつき |
| SR（回帰） | 48.93 | 99.5% | 回帰で説明できた |
| Se（残差） | 0.27 | 0.5% | 説明できなかった |
全バラつき（ST = 49.20）のうち、99.5%（SR = 48.93）が重回帰式で説明できていることがわかります。
これは非常に当てはまりの良いモデルです。決定係数 R² = 48.93/49.20 = 0.995 となります。
✅ 検算：ST = SR + Se になっているか？
ちゃんと一致しています！計算が正しいことが確認できました。
⚡ 簡便法：統計量から直接計算
実は、正規方程式で使った統計量から直接平方和を計算する公式もあります。
📐 簡便法の公式
この公式を使えば、予測値ŷを計算せずに平方和を求められます。データ数が多いときに便利です。
修正項（CT）とは？T²/Nの計算式を図解で理解する →
📋 次のステップ：分散分析表へ
平方和が求まったら、次は分散分析表を作ります。
分散分析表では、以下のことがわかります。
- 重回帰モデル全体が統計的に有意か（F検定）
- 各説明変数がどれだけ貢献しているか
【分散分析表のプレビュー】
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F値 |
|---|---|---|---|---|
| 回帰 R | 48.93 | ? | ? | ? |
| 残差 e | 0.27 | ? | ? | − |
| 計 T | 49.20 | ? | − | − |
次の記事で、この「?」の部分を埋めていきます！
【完全図解】自由度とは？｜「なぜn-1で割るのか」を中学生でも分かるように解説 →
📋 まとめ
この記事では、重回帰分析の「平方和の分解」を解説しました。
- 平方和は「バラつきの大きさ」を表す指標
- ST = SR + Se（全体 = 説明できた + 説明できない）
- ST：yの全バラつき（総平方和）
- SR：回帰で説明できたバラつき（回帰平方和）
- Se：説明できなかったバラつき（残差平方和）
- SR/ST（＝決定係数R²）が大きいほど良いモデル
平方和の分解は、「回帰式がどれだけ役に立っているか」を評価する第一歩です。
次は、この平方和を使って分散分析表を完成させ、F検定で回帰モデルの有意性を判定しましょう。
📚 次に読むべき記事
相関と回帰の「違い」がわかったら、次は中身に進みましょう。今のあなたの状態に近いところから読むのがおすすめです。
🗺️ 迷ったらまずコレ🔍 STEP1：まずは「相関」をもっと深く
📈 STEP2：単回帰の「中身」を理解する
🚀 STEP3：実務レベルへ進む
💡 おすすめの進み方：まず STEP1 の3本で「相関」を固め、STEP2 で単回帰の中身を理解し、余力があれば STEP3 へ。順番に迷ったら、いつでも上のロードマップに戻ってきてください。