- 重回帰分析をやってみたけど、このモデルって本当に使えるの?
- F検定って聞いたことあるけど、何を検定してるの?
- F値の計算方法がよくわからない…
- 重回帰モデルの「有意性検定」が何を判定しているのか
- F値の計算方法を具体的な数値例で完全理解
- F表の見方と判定の仕方
「重回帰分析で予測式を作ったけど、これって本当に意味あるの?」
そんな疑問、めちゃくちゃ大事です。
実は、どんなにキレイな回帰式ができても、「たまたま」そう見えているだけかもしれません。説明変数(x)と目的変数(y)に本当は何の関係もないのに、偶然うまくフィットしてしまうことがあるんです。
そこで登場するのが「重回帰モデルの有意性検定」です。
この検定を使えば、「このモデルは偶然じゃない、ちゃんと意味がある!」と統計的に証明できます。
この記事では、F検定の考え方から計算方法、判定基準まで、具体的な数値例を使って徹底解説します。中学生でもわかるように、イメージで説明していきますね。
重回帰モデルの有意性検定とは?
「モデル全体」が役に立つかを判定する検定
重回帰モデルの有意性検定とは、ひとことで言うと「作った予測モデル全体が、そもそも使い物になるのか?」を判定する検定です。
たとえば、あなたが「売上」を予測するために「広告費」と「店舗面積」という2つの変数を使って重回帰モデルを作ったとします。
このとき、こんな疑問が浮かびませんか?
- 広告費と店舗面積は、本当に売上と関係あるの?
- この2つの変数を使うことに意味はあるの?
- もしかして、全部「偶然」じゃない?
この疑問に統計的に答えるのが、有意性検定(F検定)です。
「すべての説明変数が目的変数に影響を与えていない」と仮定したとき、
今回のデータが得られる確率は十分に低いか?
もし「十分に低い」なら、「すべて影響なし」という仮定は間違っている → つまり「少なくとも1つの変数は効いている」と結論できます。
「天気予報」で考えるとわかりやすい
有意性検定のイメージを、天気予報で考えてみましょう。
ある気象予報士が「気温」と「湿度」から「降水確率」を予測するモデルを作りました。
でも、こんな疑問がありますよね。
- 気温と湿度は、本当に降水確率と関係あるの?
- このモデルは「サイコロを振る」より当たるの?
有意性検定は、まさにこの「サイコロより当たるか?」を判定します。
有意性検定に合格 → 「ちゃんと予測できてる!サイコロより全然マシ!」
有意性検定に不合格 → 「これ、サイコロ振ってるのと変わらないじゃん…」
帰無仮説と対立仮説を設定する
統計的検定では、まず「帰無仮説」と「対立仮説」を設定します。
重回帰モデルの有意性検定では、次のように設定します。
| 仮説 | 内容 |
|---|---|
| 帰無仮説 H₀ | すべての偏回帰係数 = 0 (どの説明変数もyに影響を与えていない) |
| 対立仮説 H₁ | 少なくとも1つの偏回帰係数 ≠ 0 (少なくとも1つの説明変数がyに影響を与えている) |
つまり、「全部意味なし」を否定できれば、「少なくとも1つは意味あり」と言えるわけです。
有意性検定に合格しても、「すべての変数が効いている」とは限りません。「少なくとも1つは効いている」ことがわかるだけです。どの変数が効いているかは、別途「偏回帰係数のt検定」で調べます。
F値の考え方|「説明できた」vs「説明できなかった」
yのバラつきを2つに分解する
F検定の考え方を理解するには、まず「yのバラつきの分解」を知る必要があります。
目的変数yには、当然バラつきがありますよね。売上データなら、高い日もあれば低い日もある。
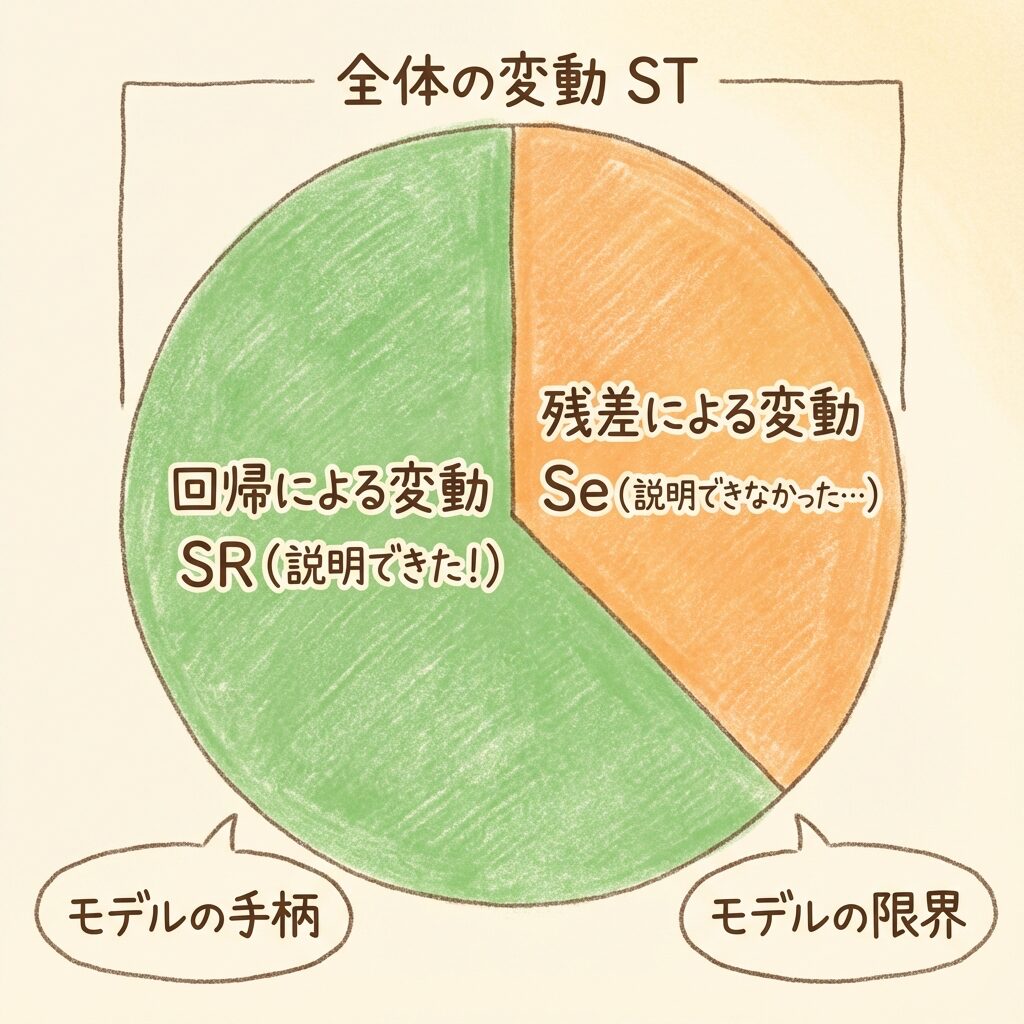
このバラつき(全体の変動)は、次の2つに分解できます。
全体の変動(ST) = 回帰による変動(SR) + 残差による変動(Se)
| 変動 | 意味 | イメージ |
|---|---|---|
| 回帰による変動 SR |
説明変数で「説明できた」バラつき | モデルの手柄 |
| 残差による変動 Se |
説明変数で「説明できなかった」バラつき | モデルの限界(誤差) |
要するに、「yがバラつく理由」を「モデルで説明できた分」と「説明できなかった分(残差)」に分けるわけです。

F値は「手柄」と「誤差」の比率
さて、ここからがF検定の核心です。
もしモデルが本当に役に立っているなら、「説明できた変動」が「説明できなかった変動」よりも大きいはずですよね。
この「大きさの比率」を数値化したのがF値です。
ここで「平均平方」という言葉が出てきました。これは「平方和を自由度で割ったもの」です。
なぜ平方和そのままではなく、自由度で割るのか?
それは、変数の数が違うと平方和の大きさが変わってしまうからです。公平に比較するために、自由度で割って「1変数あたりの変動」に揃えるわけです。
平均平方 = 平方和 ÷ 自由度
これは「1自由度あたりの変動の大きさ」を表しています。
テストの点数を「1問あたりの得点」に直すようなイメージです。
F値が大きいほど「モデルは優秀」
F値の意味を整理しましょう。
| F値の大きさ | 意味 |
|---|---|
| F値が大きい | 回帰による変動 >> 残差による変動 → モデルがyのバラつきをよく説明できている |
| F値が小さい(1に近い) | 回帰による変動 ≒ 残差による変動 → モデルは誤差と同程度しか説明できていない |
F値が十分に大きければ、「このモデルは偶然じゃない、ちゃんと意味がある」と判定できます。
では、「十分に大きい」とは具体的にどのくらいでしょうか?
その基準を与えてくれるのがF分布表です。
【計算例】F値を実際に求めてみよう
問題設定:売上を予測するモデル
具体的な数値例で計算してみましょう。
あるお店の売上(y)を、「広告費(x₁)」と「店舗面積(x₂)」で予測するモデルを作りました。
- サンプルサイズ:n = 15
- 説明変数の数:k = 2(広告費、店舗面積)
- 全体の平方和:ST = 1200
- 回帰の平方和:SR = 1000
- 残差の平方和:Se = 200
この情報から、F値を計算していきます。
ステップ1:自由度を求める
まず、それぞれの自由度を計算します。
| 自由度 | 計算式 | 計算結果 |
|---|---|---|
| 回帰の自由度 φR | k(説明変数の数) | 2 |
| 残差の自由度 φe | n − k − 1 | 15 − 2 − 1 = 12 |
| 全体の自由度 φT | n − 1 | 15 − 1 = 14 |
回帰の自由度 = 説明変数の数 k
残差の自由度 = n − k − 1(データ数 − 説明変数の数 − 1)
全体の自由度 = n − 1
「回帰 + 残差 = 全体」になっていることを確認しましょう(2 + 12 = 14 ✓)
ステップ2:平均平方を求める
次に、平方和を自由度で割って「平均平方」を求めます。
ステップ3:F値を計算する
最後に、F値を計算します。
F値は 30.0 と計算できました。
これが「大きい」のか「小さい」のか、次のステップで判定します。
ステップ4:分散分析表にまとめる
ここまでの計算結果を分散分析表にまとめましょう。
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F値 |
|---|---|---|---|---|
| 回帰 | 1000 | 2 | 500 | 30.0 |
| 残差 | 200 | 12 | 16.67 | − |
| 全体 | 1200 | 14 | − | − |

F表と比較して判定する
F分布表の見方
計算したF値(F₀ = 30.0)が「大きい」かどうかを判定するには、F分布表を使います。
F分布表は、次の3つの情報で引きます。
- 有意水準α:通常は 0.05(5%)または 0.01(1%)
- 分子の自由度:回帰の自由度 = 2
- 分母の自由度:残差の自由度 = 12
有意水準5%のF分布表を見ると、φ₁ = 2、φ₂ = 12 のとき:
F(2, 12; 0.05) = 3.89
判定:F₀ > F表 なら「有意」
さあ、いよいよ判定です。
| 比較対象 | 値 |
|---|---|
| 計算したF値(F₀) | 30.0 |
| F表の値(臨界値) | 3.89 |
F₀ = 30.0 > F表 = 3.89 なので…
このモデルは有意水準5%で「有意である」と判定できる
つまり、「広告費と店舗面積は売上と関係ない」という仮説は否定され、「少なくともどちらかは売上に影響を与えている」と結論できます。
F₀ > F表 → 有意(帰無仮説を棄却)
→ 「このモデルは使える!」
F₀ ≦ F表 → 有意でない(帰無仮説を棄却できない)
→ 「このモデルは偶然かもしれない…」
決定係数R²との関係
F値と決定係数は「同じこと」を別の角度から見ている
実は、F値と決定係数R²には密接な関係があります。
決定係数R²は「全体の変動のうち、回帰で説明できた割合」でしたね。
このモデルは、売上のバラつきの83.3%を説明できていることになります。
F値が大きい ⇔ R²が大きい、という関係があります。どちらも「モデルの説明力が高い」ことを示していますが、F検定は「統計的に意味があるか」を判定できる点が違います。
サンプルサイズが小さいと、R²が高くても「偶然」の可能性があります。F検定を行うことで、統計的な裏付けを得ることが大切です。
まとめ
この記事では、重回帰モデルの有意性検定(F検定)について解説しました。
- 有意性検定は「モデル全体が使えるか」を判定する
- F値 = 回帰の平均平方 ÷ 残差の平均平方
- F₀ > F表 なら「有意」→ モデルは偶然ではない
- 有意でも「どの変数が効いているか」は別途t検定で調べる
有意性検定に合格したら、次は「どの変数が効いているか」を調べる「偏回帰係数のt検定」に進みましょう。
📚 次に読むべき記事
偏回帰係数の意味を直感的に理解する
個々の変数の有意性を検定する方法
重回帰分析の基礎から復習したい方へ
