📝 こんな疑問を持っていませんか?
- 🎲「このサイコロ、本当に公平なの?」と疑問に思ったことがある
- 🤔「適合度の検定」って名前は聞くけど、何をする検定かわからない
- 📊データが「期待通りかどうか」を統計的に判断する方法を知りたい
- 💭カイ二乗検定の計算方法がよくわからない
✨ この記事の結論
適合度の検定は「データが期待通りの分布に従っているか」を確かめる検定です。
「期待値」と「実測値」のズレをカイ二乗(χ²)値で数値化し、
そのズレが「偶然の範囲内か」「偶然とは言えないほど大きいか」を判定します。
「このサイコロ、なんか6の目ばっかり出るな…イカサマじゃない?」
「うちの店、月曜日だけお客さん少ない気がする…気のせいかな?」
こんな風に、「期待していた結果」と「実際の結果」にズレがあると感じたこと、ありませんか?
でも、そのズレが「たまたま偶然起きたもの」なのか、「何か原因があって起きたもの」なのか、感覚だけでは判断できませんよね。
そんなときに使うのが、「適合度の検定」です。
この記事では、適合度の検定の考え方・計算方法・使いどころを、サイコロや来店客数など身近な例をたくさん使って、初心者の方でも「なるほど!」とイメージできるように解説していきますね。
目次
🎲 適合度の検定とは?|「期待」と「現実」のズレを測る
まずは「適合度の検定ってそもそも何?」というところから、やさしく説明していきます。
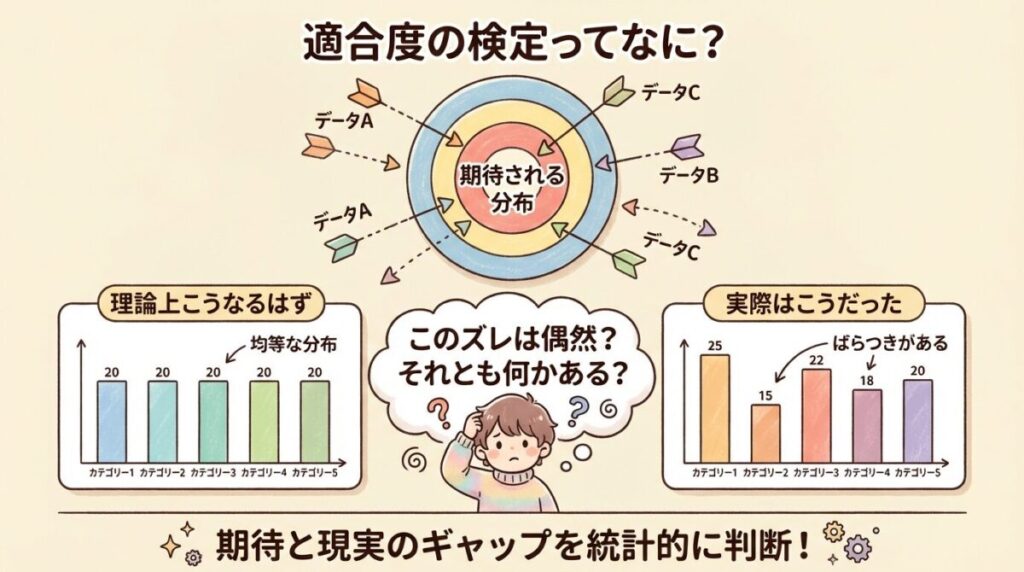
🎯 「期待される分布」と「実際の分布」を比べる検定
適合度の検定を一言で説明すると、こうなります。
📖 適合度の検定とは?
「観測されたデータの分布」が、
「理論的に期待される分布」に
適合しているかどうかを検定する方法
ちょっとわかりにくいですよね。サイコロの例で考えてみましょう。
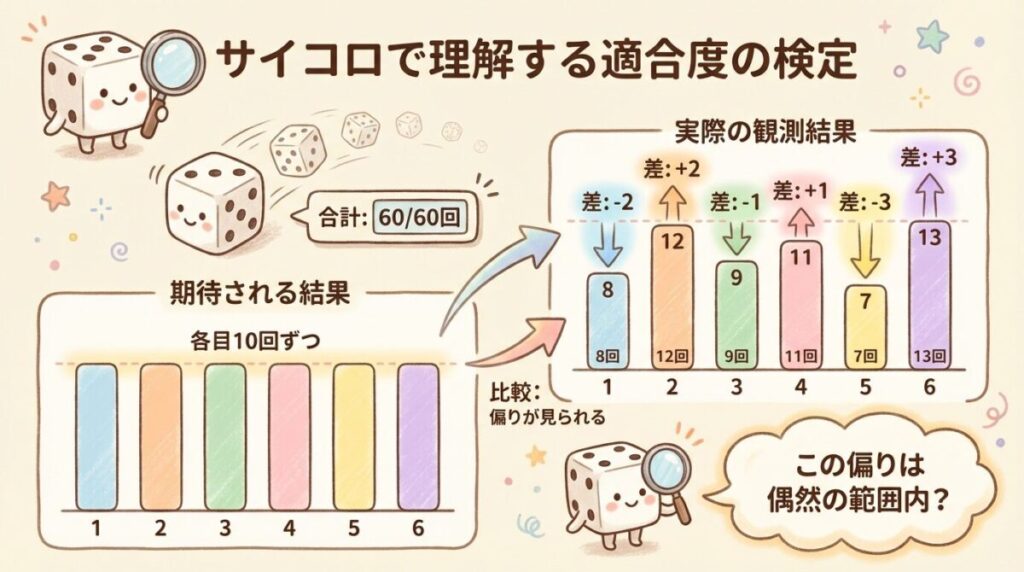
🎲 サイコロで考えてみよう
公平なサイコロを60回振ったとします。
【期待される結果】
1〜6の目がそれぞれ10回ずつ出るはず(60回 ÷ 6 = 10回)
【実際の結果】
1の目:8回、2の目:12回、3の目:9回、4の目:11回、5の目:7回、6の目:13回
🤔 「あれ?6の目が多くない?このサイコロ、イカサマ?」
→ 適合度の検定を使えば、このズレが「偶然の範囲内」か「怪しい」かを判定できます!
📊 「ズレ」を数値化するのがカイ二乗(χ²)値
適合度の検定では、「期待値」と「実測値」のズレを「カイ二乗値(χ²値)」という数値で表します。
カイ二乗値が大きいほど「ズレが大きい」、小さいほど「期待通り」という意味になります。
😊
χ²値が小さい
期待値と実測値のズレが小さい
→ 「期待通り!」
😲
χ²値が大きい
期待値と実測値のズレが大きい
→ 「何かおかしい!」
🔑 検定の流れをざっくり理解
適合度の検定の流れを、ざっくりまとめるとこうなります。
STEP 1
期待度数を計算
STEP 2
χ²値を計算
STEP 3
臨界値と比較
STEP 4
判定!
詳しい計算方法は後ほど解説しますが、まずは「期待と現実のズレを数値化して、偶然かどうか判定する」というイメージを持っておいてください。
🧪 適合度の検定の仮説|「期待通り」を疑う
統計的検定では、まず「仮説」を立てます。適合度の検定ではどんな仮説を立てるのでしょうか?
📋 帰無仮説と対立仮説
適合度の検定では、次のような仮説を立てます。
H₀:帰無仮説(きむかせつ)
「データは期待される分布に従っている」
サイコロの例:「サイコロは公平で、各目が出る確率は1/6ずつである」
H₁:対立仮説(たいりつかせつ)
「データは期待される分布に従っていない」
サイコロの例:「サイコロは公平ではなく、出やすい目がある」
検定では、「帰無仮説が正しい」と仮定して、今回のデータが得られる確率を計算します。その確率がとても低ければ、「帰無仮説は間違っている(=期待通りではない)」と判断するわけですね。
🎯 サイコロの例で仮説を整理
先ほどのサイコロの例で、仮説を整理してみましょう。
🎲 サイコロ60回の検定
帰無仮説 H₀:
サイコロは公平である(各目の出る確率は1/6)
対立仮説 H₁:
サイコロは公平ではない(出やすい目がある)
期待度数:
各目が 60回 × 1/6 = 10回ずつ出る
💡 「適合度」という名前の意味
「適合度の検定」という名前、ちょっと堅苦しいですよね。この名前の意味を理解しておきましょう。
📖 「適合度」の意味
適合度(てきごうど) = 「どれくらい適合しているか」の度合い
つまり、「実際のデータが、期待される分布にどれくらいフィット(適合)しているか」を検定するから「適合度の検定」と呼ばれます。
英語では「Goodness of Fit Test」(良さ適合検定)と呼ばれます。「Fit(フィット)」という言葉からも、「ピッタリ合っているか?」を調べる検定だとイメージできますね。
⚠️ 適合度の検定が使えるデータ
適合度の検定は、どんなデータにも使えるわけではありません。使える条件を確認しておきましょう。
✅ 適合度の検定が使える条件
1. カテゴリデータ(度数データ)であること
例:サイコロの目(1〜6)、曜日(月〜日)、血液型(A・B・O・AB)など
連続データ(身長、体重など)には直接使えません
2. 期待度数がある程度大きいこと
目安:すべてのカテゴリで期待度数が5以上
期待度数が小さいと、検定の精度が落ちます
3. 観測が独立していること
例:サイコロを振るたびに独立した試行である
1回目の結果が2回目に影響しない
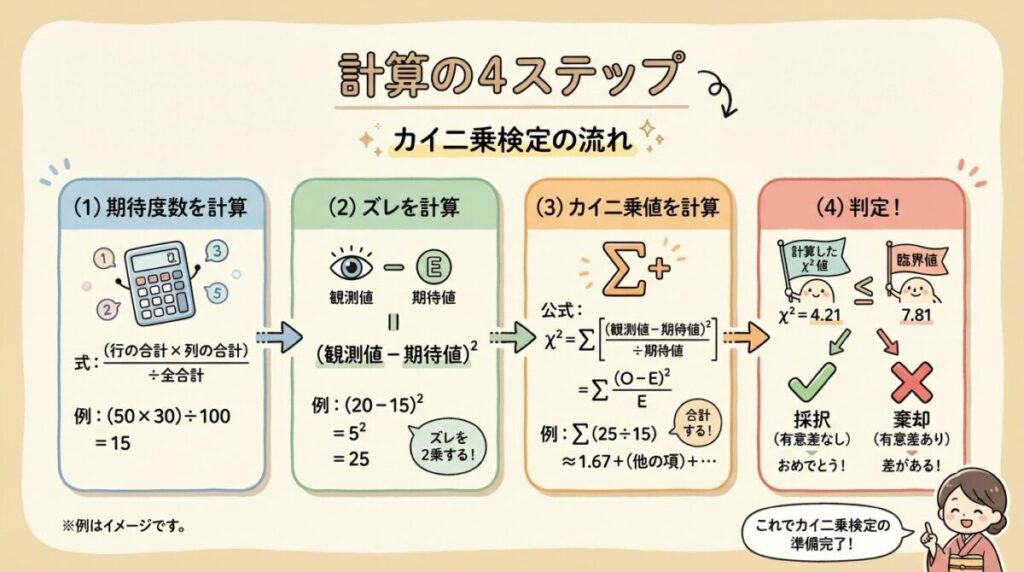
📝 適合度の検定の計算手順|4ステップで完全理解
では、実際の計算手順をサイコロの例を使って、ステップバイステップで解説していきます。
🎲 例題:サイコロは公平か?
サイコロを60回振ったところ、次の結果が得られました。
このサイコロは公平と言えるでしょうか?(有意水準5%で検定)
Step 1:期待度数を計算する
まず、「帰無仮説が正しいとしたら、各カテゴリで何回ずつ観測されるはずか」を計算します。これが「期待度数」です。
公平なサイコロなら、各目の出る確率は1/6です。60回振ったら、各目は次の回数出るはず:
期待度数 = 60回 × 1/6 = 10回(各目とも)
| 目 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 観測度数 O | 8 | 12 | 9 | 11 | 7 | 13 |
| 期待度数 E | 10 | 10 | 10 | 10 | 10 | 10 |
Step 2:各カテゴリのズレを計算する
次に、各カテゴリで「観測値と期待値のズレ」を計算します。
ただし、単純な差(O − E)だと、プラスとマイナスが打ち消し合ってしまいます。そこで、差を2乗してから、期待値で割ることで標準化します。
📐 各カテゴリのズレの計算式
(O − E)² / E
O = 観測度数(Observed)、E = 期待度数(Expected)
各目について計算してみましょう。
| 目 | O | E | O − E | (O − E)² | (O − E)² / E |
|---|---|---|---|---|---|
| 1 | 8 | 10 | −2 | 4 | 0.40 |
| 2 | 12 | 10 | +2 | 4 | 0.40 |
| 3 | 9 | 10 | −1 | 1 | 0.10 |
| 4 | 11 | 10 | +1 | 1 | 0.10 |
| 5 | 7 | 10 | −3 | 9 | 0.90 |
| 6 | 13 | 10 | +3 | 9 | 0.90 |
Step 3:カイ二乗値(χ²)を計算する
Step 2で計算した各カテゴリのズレをすべて合計したものが、カイ二乗値(χ²)です。
📐 カイ二乗値の計算式
χ² = Σ (O − E)² / E
Σ(シグマ)= すべてのカテゴリについて合計
計算してみましょう。
χ² = 0.40 + 0.40 + 0.10 + 0.10 + 0.90 + 0.90
χ² = 2.80
Step 4:臨界値と比較して判定する
最後に、計算したχ²値を「カイ二乗分布表」の臨界値と比較します。
まず、自由度を求めます。
自由度 = カテゴリ数 − 1 = 6 − 1 = 5
※ なぜ「−1」するかは、合計が固定されているため1つの値が自動的に決まるから
有意水準5%、自由度5のカイ二乗分布の臨界値は11.07です。
🎯 判定
計算したχ²値
2.80
臨界値(α=0.05, df=5)
11.07
χ² = 2.80 < 臨界値 11.07
→ 帰無仮説を棄却できない
→ 「サイコロは公平である」と言える!
今回のデータでは、期待値とのズレは偶然の範囲内と判断されました。つまり、このサイコロは「統計的には公平」と言えます。
💡 判定の考え方
χ² < 臨界値 → ズレは小さい → 期待通り(帰無仮説を採択)
χ² ≥ 臨界値 → ズレは大きい → 期待と違う!(帰無仮説を棄却)
🏪 実践例|来店客数の曜日分布を検定してみよう
サイコロの例は理解できたけど、「実務ではどう使うの?」と思いますよね。
もう一つ、ビジネスで使える実践例を見てみましょう。
🏪 例題:来店客数は曜日で違う?
あるカフェの店長が「月曜日はお客さんが少ない気がする」と感じています。
1週間の来店客数を調べたところ、次の結果でした。
来店客数は曜日によって違うと言えるでしょうか?(有意水準5%)
📋 仮説を立てる
H₀:帰無仮説
来店客数は曜日によらず均等である
(各曜日の来店確率は1/7)
H₁:対立仮説
来店客数は曜日によって異なる
(来店しやすい曜日がある)
📝 計算してみよう
期待度数:400人 ÷ 7曜日 ≒ 57.14人(各曜日)
| 曜日 | O(観測) | E(期待) | O − E | (O − E)² | (O − E)² / E |
|---|---|---|---|---|---|
| 月 | 35 | 57.14 | −22.14 | 490.18 | 8.58 |
| 火 | 48 | 57.14 | −9.14 | 83.54 | 1.46 |
| 水 | 52 | 57.14 | −5.14 | 26.42 | 0.46 |
| 木 | 45 | 57.14 | −12.14 | 147.38 | 2.58 |
| 金 | 60 | 57.14 | +2.86 | 8.18 | 0.14 |
| 土 | 85 | 57.14 | +27.86 | 776.18 | 13.58 |
| 日 | 75 | 57.14 | +17.86 | 318.98 | 5.58 |
| 合計(χ²) | 32.38 | ||||
🎯 判定
自由度 = 7 − 1 = 6
有意水準5%、自由度6の臨界値 = 12.59
🎯 判定結果
計算したχ²値
32.38
臨界値(α=0.05, df=6)
12.59
χ² = 32.38 > 臨界値 12.59
→ 帰無仮説を棄却!
→ 「来店客数は曜日によって異なる」と言える!
店長の勘は正しかった!来店客数には曜日による偏りがあることが統計的に確認できました。月曜日は少なく、土日は多いという傾向が、偶然ではないと言えます。
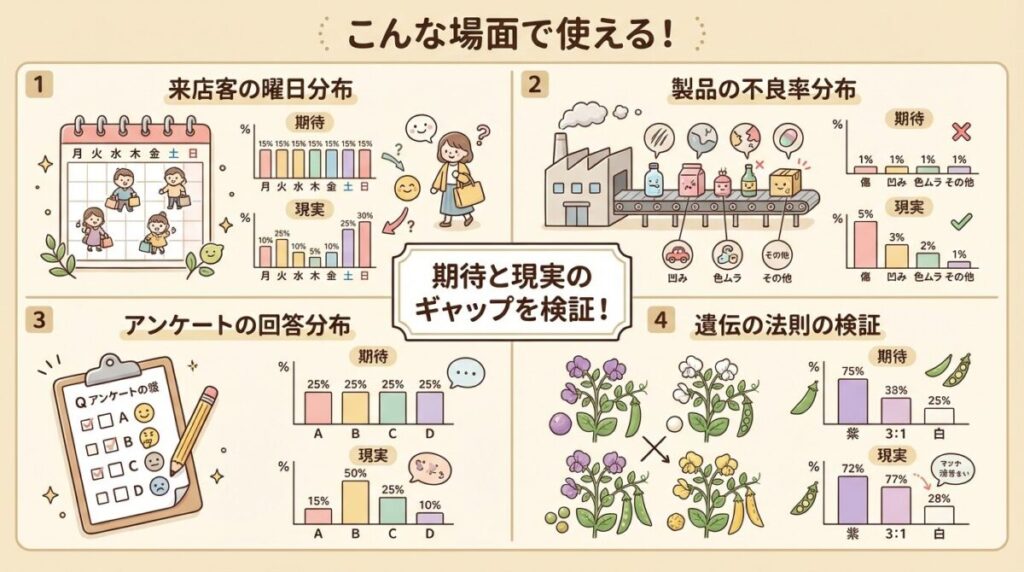
🎯 適合度の検定はこんな場面で使える!
適合度の検定は、「期待される分布」と「実際の分布」を比較したいあらゆる場面で使えます。
🎲
ギャンブル・ゲームの公平性
サイコロ、ルーレット、カードの配布などが公平かどうかを検証
🏭
製造業の品質管理
不良品の発生が特定の時間帯・ラインに偏っていないかを確認
📊
マーケティング調査
アンケート回答が期待通りの分布になっているか、偏りがないかを検証
🧬
遺伝学・生物学
メンデルの法則(3:1など)通りの分離比になっているかを検証
📞
コールセンター・人員配置
問い合わせが時間帯によって均等か、偏りがあるかを分析
🔢
乱数・シミュレーション
乱数生成器が本当にランダムな数を出しているかを検証
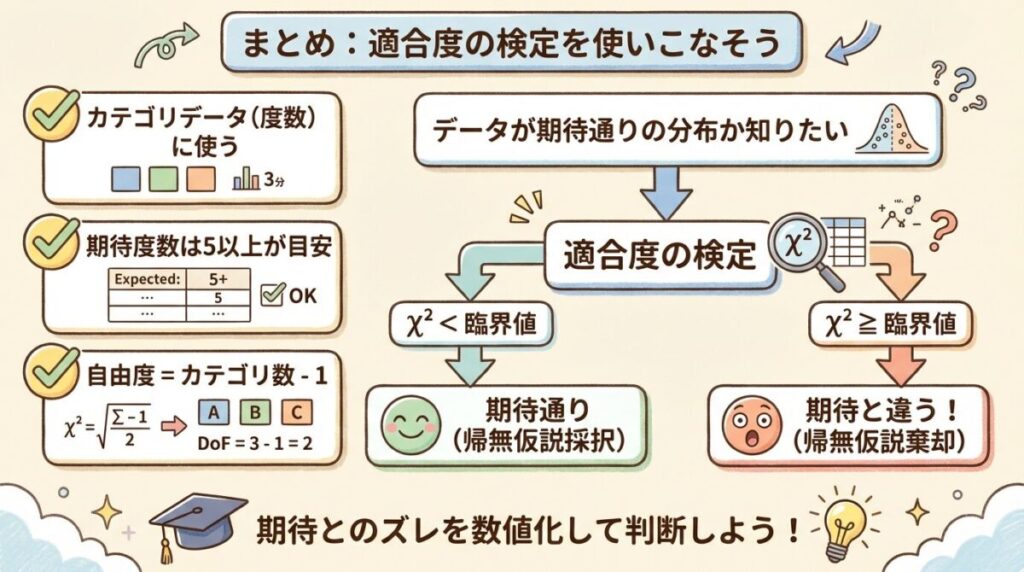
📝 まとめ|適合度の検定を使いこなそう
最後に、この記事のポイントをまとめます。
✅ この記事のまとめ
1. 適合度の検定とは:観測データが「期待される分布」に適合しているかを検定する方法。カイ二乗検定の一種。
2. カイ二乗値(χ²):期待値と実測値のズレを数値化したもの。大きいほどズレが大きい。
3. 計算式:χ² = Σ(O − E)² / E (Oは観測度数、Eは期待度数)
4. 自由度:カテゴリ数 − 1
5. 判定:χ² ≥ 臨界値 なら「期待と異なる」、χ² < 臨界値 なら「期待通り」
🎯 適合度の検定フローチャート
↓
↓
期待通り!
期待と違う!
⚠️ 使用上の注意点
- 期待度数は5以上が目安:期待度数が小さいカテゴリがあると、検定の精度が落ちます
- カテゴリデータ専用:連続データ(身長、体重など)には直接使えません
- 独立性の検定との違い:適合度の検定は「1つの変数の分布」を見る検定です。「2つの変数の関連」を見る場合は「独立性の検定」を使います
適合度の検定は、「期待と現実のギャップ」を統計的に評価できる強力なツールです。「なんとなく偏っている気がする…」という感覚を、数字で裏付けることができますよ。
QC検定でもよく出題されるテーマですので、ぜひ計算手順をマスターしておいてくださいね。
📚 次に読むべき記事
🔗 適合度の検定とセットで学ぼう
【完全図解】独立性の検定とは?|2つの変数に関連があるかを統計で確かめる方法
適合度の検定が「1つの変数の分布」を見るのに対し、独立性の検定は「2つの変数の関連」を見ます。セットで理解しましょう。
📊 データの可視化を学びたい方へ
【完全図解】ヒストグラムとは?|データの「形」が一目でわかる最強のグラフ
検定の前に、まずデータの分布を可視化することが大切。ヒストグラムの作り方・読み方をマスターしましょう。