- 分割法で「誤差が2つある」意味がわからない
- 1次誤差と2次誤差、どっちで検定するのか混乱する
- 分割法の自由度計算が複雑すぎて手が止まる
- プーリング後の点推定で何をすればいいかわからない
- 分割法が必要になる場面と「2つの誤差」の直感的な意味
- 1次単位・2次単位の見分け方
- 分散分析表の作り方と検定の手順
- 最適条件の決め方と点推定の計算方法
目次
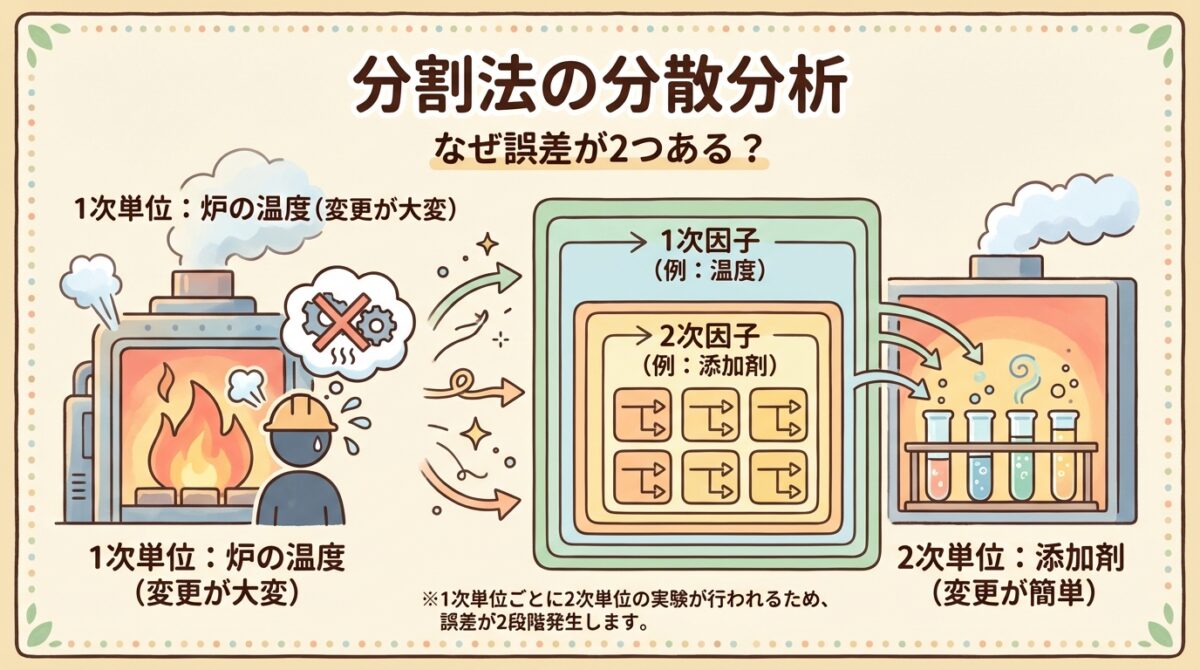
分割法とは?「変えにくい因子」がある実験の設計法
通常の実験計画法では、すべての因子の水準を完全にランダムな順序で変えて実験します。しかし現実の工場では、「この因子は変更に時間がかかる」「この設備は一度設定したら簡単に変えられない」という制約があります。
そんなとき使うのが分割法(Split-plot design)です。
🏭 具体例:焼成炉の温度と添加剤の実験
こんな状況をイメージしてください。
あなたは陶器工場の品質管理担当者です。
製品の強度を上げるため、2つの因子を検討しています。
- 因子A:焼成炉の温度(800℃、900℃、1000℃の3水準)
- 因子B:添加剤の種類(X、Y、Zの3水準)
ここで問題があります。炉の温度変更には2時間かかるのです。一方、添加剤の変更は5分で済みます。
もし完全ランダム化で実験すると、「800℃→900℃→800℃→1000℃→900℃…」と温度を頻繁に変える必要があり、膨大な時間がかかります。
そこで分割法では、こう考えます。
「温度はまとめて設定して、その中で添加剤だけランダムに変える」
→ 800℃に設定したら、その温度のまま添加剤X→Y→Zを実験
→ 次に900℃に変更して、また添加剤X→Y→Zを実験
→ これなら温度変更は最小限で済む!
この「変えにくい因子をまとめて、変えやすい因子をその中で変える」という構造が、分割法の本質です。
分割法とは?複雑な条件を整理するための実験設計 →
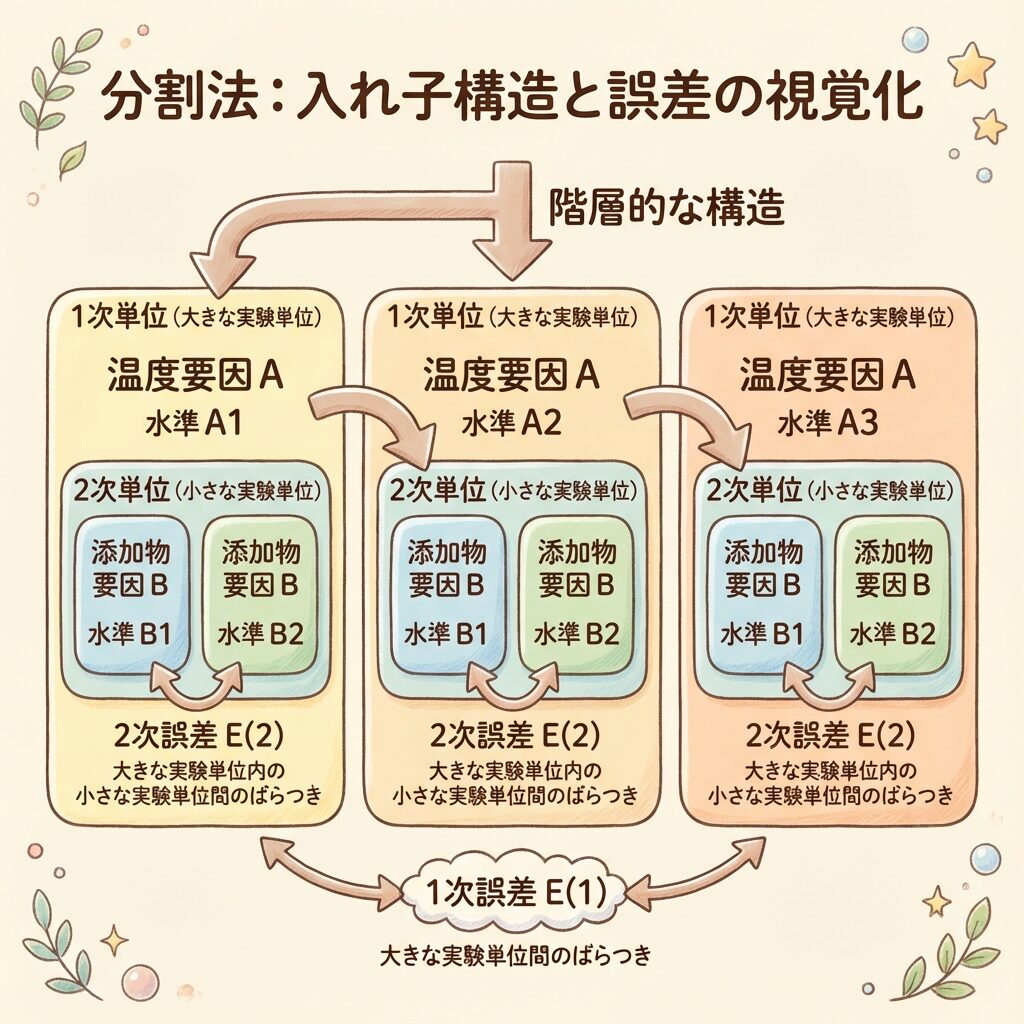
1次単位と2次単位:「入れ子構造」で理解する
分割法を理解する鍵は、「入れ子構造(ネスト構造)」をイメージすることです。マトリョーシカ人形のように、大きな箱の中に小さな箱が入っている構造です。
📦 1次単位(大きな箱)と2次単位(小さな箱)
| 用語 | 意味 | 焼成炉の例 | 特徴 |
|---|---|---|---|
| 1次単位 | 大きな実験単位 | 「800℃の炉」全体 | 変更しにくい |
| 2次単位 | 小さな実験単位 | 炉の中の各試験片 | 変更しやすい |
| 1次因子 | 1次単位に割り付ける因子 | 温度(A) | 変更に時間がかかる |
| 2次因子 | 2次単位に割り付ける因子 | 添加剤(B) | 簡単に変更できる |
🔑 見分け方のコツ
問題文を読むとき、以下のキーワードに注目してください。
・「水準変更に時間がかかる」
・「まとめて設定する」
・「ランダムな順序で水準を設定後、各水準で〜」
・「設備の都合上、変更が困難」
・「各組合せでランダムな順序で実験」
・「1次単位の中で変化させる」
・「簡単に変更できる」
なぜ誤差が2つ必要なのか?
分割法の最大の特徴は、「1次誤差」と「2次誤差」の2種類の誤差があることです。これが多くの人を混乱させるポイントですが、実は理由は単純です。
🎯 「バラつきの発生源」が2つあるから
焼成炉の実験で考えてみましょう。
1次誤差(炉ごとのバラつき)
同じ800℃設定でも、「月曜に使った炉」と「水曜に使った炉」では微妙に状態が違うかもしれません。炉の個体差、日による環境変化など、1次単位(炉)ごとのバラつきです。
2次誤差(炉の中でのバラつき)
同じ炉の中でも、置く場所によって温度ムラがあるかもしれません。添加剤の混ぜ具合の差もあるでしょう。同じ1次単位の中での2次単位間のバラつきです。
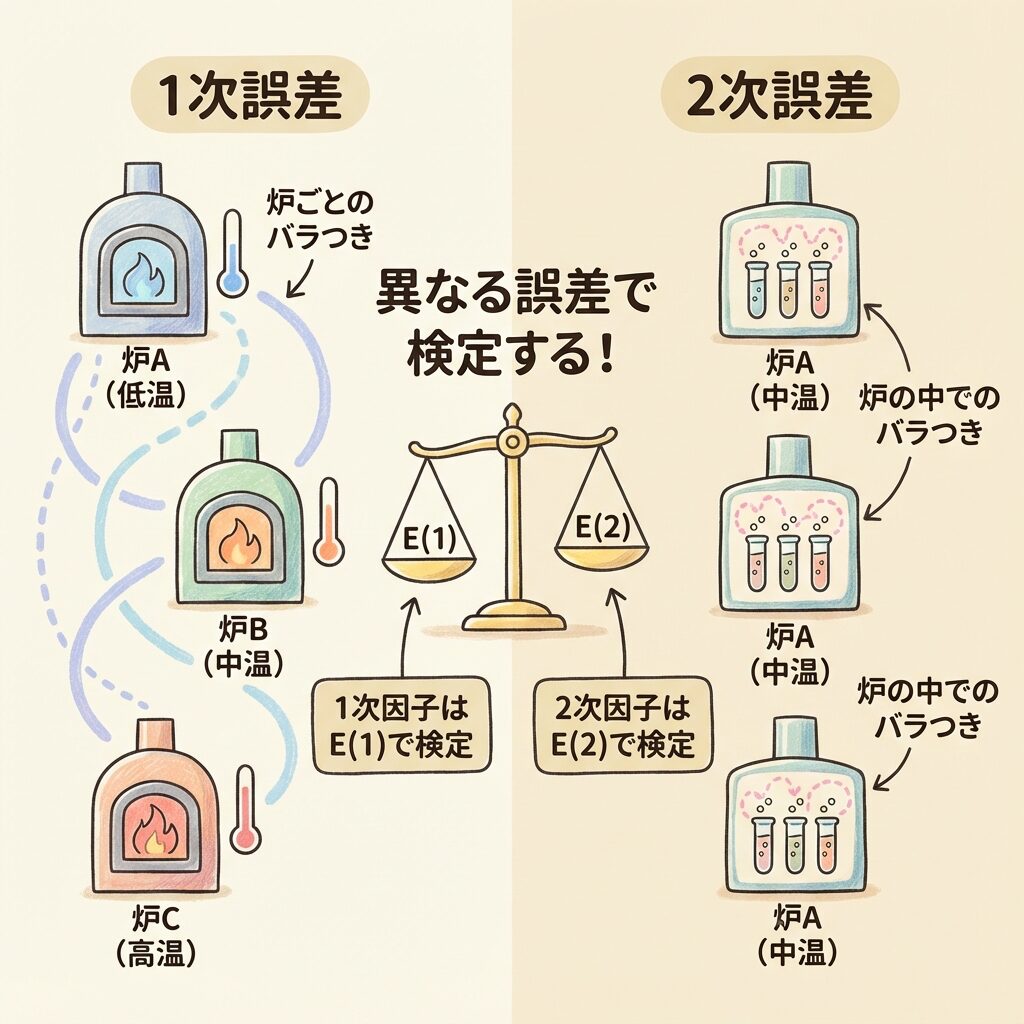
この2つのバラつきは性質が異なるので、別々に評価する必要があります。
1次因子(温度)の効果 → 1次誤差E(1)で検定
2次因子(添加剤)の効果 → 2次誤差E(2)で検定
これを間違えると、検定結果が正しくなりません!
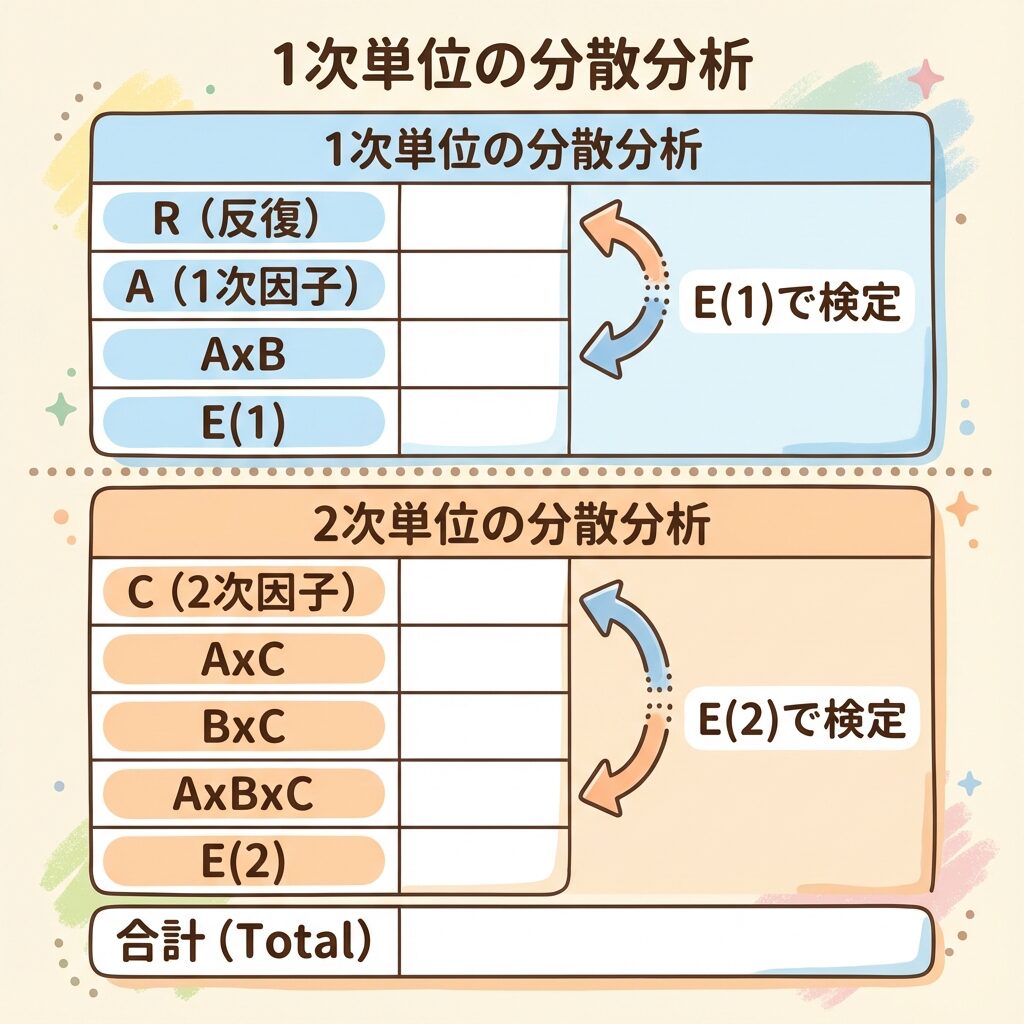
分割法の分散分析表:構造を理解する
分割法の分散分析表は、「1次単位の分析」と「2次単位の分析」が上下に分かれた構造になっています。
📊 分散分析表の基本構造
以下は、1次因子A(3水準)、2次因子B(3水準)、反復R(2回)の場合の例です。
| 1次単位の分散分析 | ||||
|---|---|---|---|---|
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F₀ |
| R(反復) | S_R | r−1 = 1 | V_R | V_R / V_E(1) |
| A(1次因子) | S_A | a−1 = 2 | V_A | V_A / V_E(1) |
| E(1)(1次誤差) | S_E(1) | (r−1)(a−1) = 2 | V_E(1) | — |
| 2次単位の分散分析 | ||||
|---|---|---|---|---|
| 要因 | 平方和 S | 自由度 φ | 平均平方 V | F₀ |
| B(2次因子) | S_B | b−1 = 2 | V_B | V_B / V_E(2) |
| A×B(交互作用) | S_AB | (a−1)(b−1) = 4 | V_AB | V_AB / V_E(2) |
| E(2)(2次誤差) | S_E(2) | a(r−1)(b−1) = 6 | V_E(2) | — |
| T(総計) | S_T | n−1 = 17 | — | — |
・1次因子AのF値 = V_A ÷ V_E(1)(1次誤差で割る)
・2次因子BのF値 = V_B ÷ V_E(2)(2次誤差で割る)
・交互作用A×BのF値 = V_AB ÷ V_E(2)(2次誤差で割る)
どの誤差で割るかを間違えないことが最重要です。
📝 自由度の計算パターン
自由度の計算は、分割法特有のパターンがあります。
| 要因 | 自由度の公式 | 覚え方 |
|---|---|---|
| 1次因子A | a − 1 | 水準数 − 1 |
| 2次因子B | b − 1 | 水準数 − 1 |
| 反復R | r − 1 | 反復数 − 1 |
| 交互作用A×B | (a−1)(b−1) | 各自由度の積 |
| 1次誤差E(1) | (r−1)(a−1) | 反復×1次因子 |
| 2次誤差E(2) | a(r−1)(b−1) | 残り、または公式 |
分割法の問題を解く6ステップ
分割法の問題は、以下の手順で解けば必ず正解にたどり着けます。
📋 Step 1:実験の構造を把握する
まず問題文を読んで、以下を特定します。
- 1次因子は何か?(変更しにくい因子)
- 2次因子は何か?(変更しやすい因子)
- 各因子の水準数は?
- 反復(繰返し)の回数は?
「〇〇の水準の組合せをランダムに設定後、各組合せで△△を…」という記述があれば、〇〇が1次因子、△△が2次因子です。
📋 Step 2:自由度を計算する
すべての要因と誤差の自由度を計算します。最後に合計が総自由度(n−1)と一致するか確認しましょう。
📋 Step 3:平方和を計算する
二元表・三元表を使って、各要因の平方和を計算します。修正項CTを引くことを忘れずに。
📋 Step 4:分散分析表を完成させる
平均平方(V = S ÷ φ)を計算し、F値を求めます。どの誤差で割るかを間違えないように注意!
📋 Step 5:プーリングを判断する
有意でない要因は、誤差にプール(併合)します。
・1次単位の有意でない要因 → 1次誤差E(1)にプール
・2次単位の有意でない要因 → 2次誤差E(2)にプール
1次の要因を2次誤差にプールしてはいけません(逆も同様)。
📋 Step 6:最適条件と点推定を求める
有意な因子について、最適な水準を決定し、その条件での特性値を推定します。
・望大特性(大きいほど良い)→ 平均が最大の水準を選ぶ
・望小特性(小さいほど良い)→ 平均が最小の水準を選ぶ
・望目特性(目標値がある)→ 目標値に最も近い水準を選ぶ
交互作用が有意な場合は、因子の組合せで考える必要があります。
点推定の計算方法
最適条件での特性値の点推定は、「有意な効果だけを積み上げる」という考え方で計算します。
📐 基本の点推定公式
μ̂ = T̄ + (Āᵢ − T̄) + (B̄ⱼ − T̄)
= Āᵢ + B̄ⱼ − T̄
T̄:総平均 / Āᵢ:最適水準Aᵢの平均 / B̄ⱼ:最適水準Bⱼの平均
μ̂ = (AᵢBⱼの平均)
交互作用が有意な場合は、因子を個別に考えず、組合せの平均をそのまま使います。
🎯 点推定の考え方
点推定の式は、以下のように分解して考えると理解しやすくなります。
μ̂ = 総平均 + Aの効果 + Bの効果
= T̄ + (Āᵢ − T̄) + (B̄ⱼ − T̄)
各因子の「効果」とは、「その水準の平均」−「総平均」です。
つまり、「全体の平均からどれだけズレているか」を足し合わせます。
まとめ:分割法の攻略ポイント
- 分割法は「変更しにくい因子」がある実験で使う
- 1次単位(大きな箱)の中に2次単位(小さな箱)がある入れ子構造
- 誤差は2種類:1次誤差E(1)と2次誤差E(2)
- 1次因子はE(1)で、2次因子はE(2)で検定する(最重要!)
- プーリングは同じ単位の誤差にのみ行う
- 交互作用が有意なら、組合せで最適条件を考える
分割法は、一見複雑に見えますが、「入れ子構造」と「2つの誤差」さえ理解すれば、あとは通常の分散分析と同じです。
問題を解くときは、必ず「どれが1次因子で、どれが2次因子か」を最初に特定してください。それが決まれば、自由度の計算も、検定に使う誤差も、すべて自動的に決まります。
📚 次に読むべき記事
分割法の基本概念をより詳しく解説しています
分割法と混同しやすい「枝分かれ実験」との違いを解説
有意でない要因を誤差にプールする方法を詳しく解説