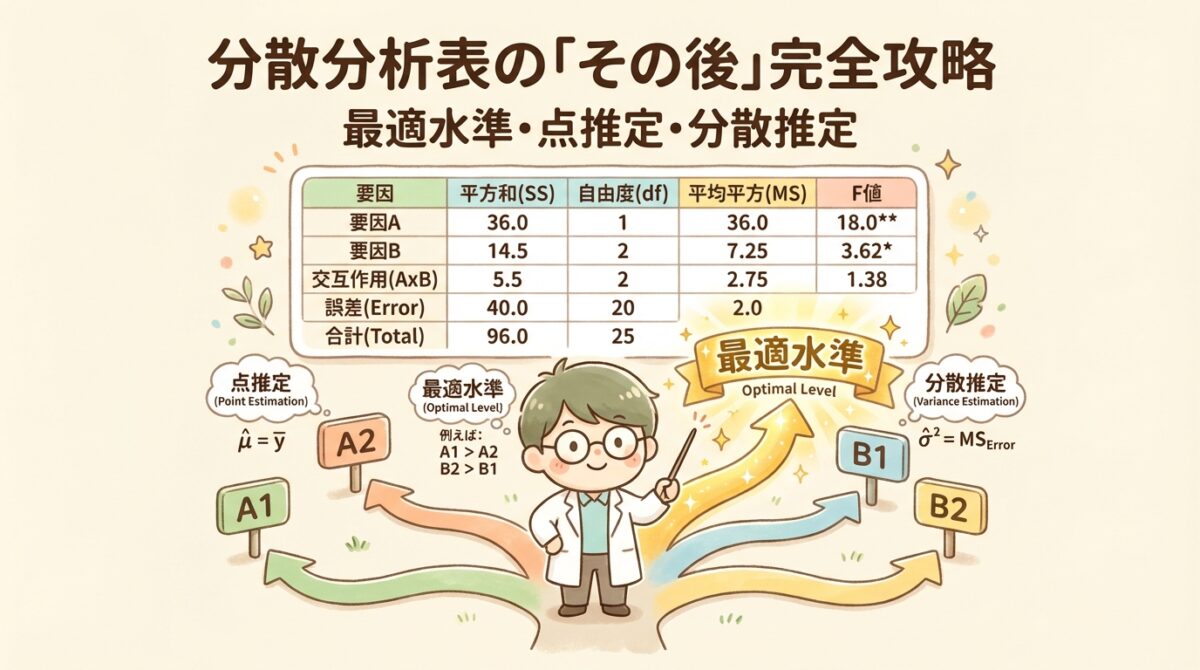
- 分散分析表は作れるけど、その後の「最適水準」の選び方がわからない
- 交互作用が有意なときと有意でないときで、水準の選び方が違う?
- 点推定値μ̂の計算式が出てきても、どの値を代入すればいいか迷う
- 「有効繰返し数ne」って何?分散の推定で毎回つまずく…
- 信頼区間の計算まで含めると、もう何が何だかわからない
- 交互作用の有意性で変わる「最適水準の選び方」のルール
- 点推定値μ̂の計算方法を「総平均+効果の和」でスッキリ理解
- 有効繰返し数neの意味と計算方法
- 分散V(μ̂)と信頼区間の求め方を例題で完全マスター
実験計画法の学習で、多くの人がつまずくポイントがあります。
それは「分散分析表を作った後、どうすればいいの?」という部分です。
分散分析表の作り方は理解できた。F検定で有意かどうかも判定できた。でも、その後に出てくる「最適水準を選べ」「点推定値を求めよ」「分散を推定せよ」という問題になると、急に手が止まってしまう…。
この記事では、分散分析表を作った「その後」の分析手順を、初歩から丁寧に解説します。特に交互作用が有意な場合の水準選択と点推定・分散推定の計算方法に焦点を当てて、「なぜそうするのか」まで含めて説明していきます。
この記事は「分散分析表の作り方」「F検定」を理解している方向けです。まだ不安な方は、先に以下の記事で基礎を固めてください。
分散分析表の作成手順を確認したい方はこちら
目次
分散分析の「その後」の全体像を把握しよう
まずは「分散分析表を作った後、何をするのか」の全体像を把握しましょう。
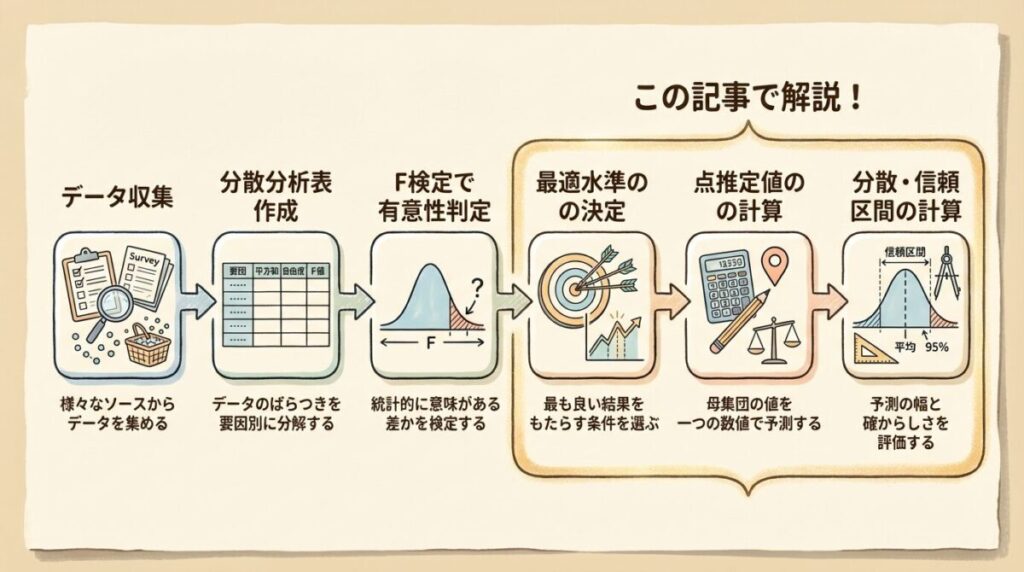
実験計画法の分析は、大きく分けて5つのステップで進みます。
実験計画法の分析フロー
実験を行い、データを表にまとめる
平方和S → 自由度φ → 分散V → F値の順で計算
交互作用の有意性に応じて水準を選ぶ ← この記事で解説!
最適水準での母平均を推定 ← この記事で解説!
推定の「精度」を評価する ← この記事で解説!
多くの教科書やQC検定の問題では、Step 1〜2までは丁寧に解説されていますが、Step 3〜5の部分は「公式だけ」で終わっていることが多いのです。
この記事では、この「後半部分」を重点的に解説していきます。
分散分析表を作るだけでは「どの因子が効いているか」がわかるだけです。実務や試験で求められるのは、「じゃあ、どの条件で実験すれば最も良い結果が得られるか?」「その結果はどれくらいの精度で予測できるか?」という答えです。Step 3〜5はその答えを出すための計算なのです。
【Step 3】最適水準の選び方|交互作用の有意性がカギ
分散分析表でF検定を行い、各因子や交互作用の有意性が判定できたら、次は「最適水準」を決めるステップです。
ここで多くの人が混乱するのが、「交互作用が有意な場合と有意でない場合で、水準の選び方が違う」という点です。
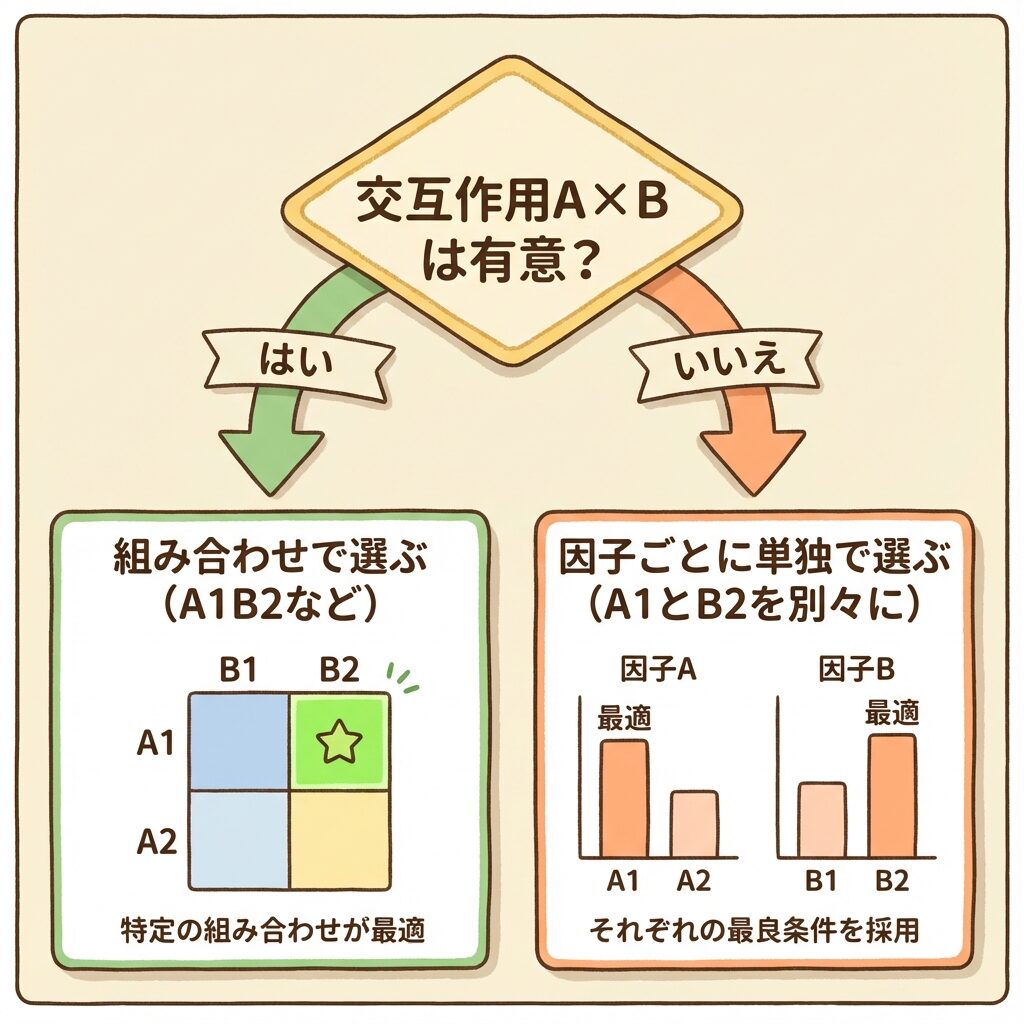
大原則:交互作用の有意性で選び方が変わる
→ AとBの「組み合わせ」で最適水準を選ぶ
(例:A₁B₂が最適、のように2つセットで決める)
→ AとBを「単独」で最適水準を選ぶ
(例:Aの最適はA₁、Bの最適はB₂、のように別々に決める)
「なぜこのようなルールになるのか」を理解するために、交互作用の意味を復習しましょう。
交互作用が「有意」とはどういうことか?
交互作用とは、「因子Aの効果が、因子Bの水準によって変わる」という現象です。
たとえば、カレーの美味しさを考えてみましょう。
因子A:ルーの種類(A₁=甘口、A₂=辛口)
因子B:肉の種類(B₁=チキン、B₂=ビーフ)
交互作用がない場合:
「辛口ルー(A₂)の方が美味しい」という効果が、肉の種類に関係なく一定。
→ チキンでもビーフでも、辛口の方が美味しい
→ AとBを別々に選んでOK(A₂を選び、Bは単独で最適なものを選ぶ)
交互作用がある場合:
「辛口ルー(A₂)の効果」が、肉の種類によって変わる。
→ チキン+辛口は微妙だけど、ビーフ+辛口は最高!
→ AとBをセットで考えないと最適解を見逃す(A₂B₂という組み合わせが最適)
交互作用とは?因子の組み合わせ効果を図解|実験計画法の基礎概念⑧ →
【ケース1】交互作用が有意な場合の水準選択
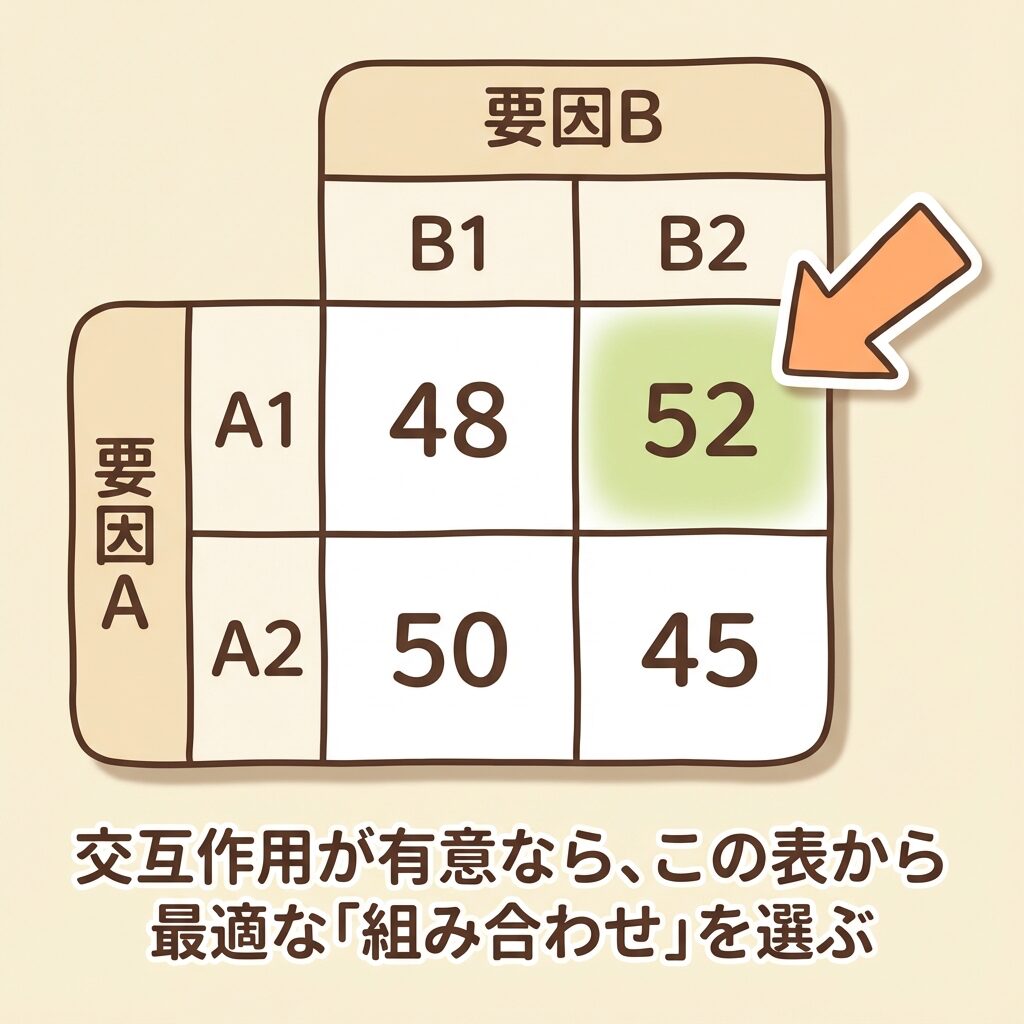
交互作用A×Bが有意と判定された場合、AとBは「組み合わせ」として最適な水準を選びます。
具体的には、二元表(水準の組み合わせ表)を作り、各セルの平均値を比較します。
手順:二元表から最適な組み合わせを選ぶ
因子A(2水準)と因子B(2水準)で実験を行い、以下の結果が得られた。
目的:特性値を大きくしたい(望大特性)
Step 1:各組み合わせの平均値を計算し、二元表を作る
| B₁ | B₂ | Aの平均 | |
|---|---|---|---|
| A₁ | 45 | 58 | 51.5 |
| A₂ | 52 | 48 | 50.0 |
| Bの平均 | 48.5 | 53.0 | 総平均 50.75 |
Step 2:最大(または最小)のセルを見つける
この例では「大きくしたい」ので、最大値を探します。
- A₁B₁ = 45
- A₁B₂ = 58 ← 最大!
- A₂B₁ = 52
- A₂B₂ = 48
交互作用A×Bが有意なので、最適水準は「A₁B₂」という組み合わせで表現する。
(「A₁が最適でB₂が最適」ではなく、「A₁B₂という組み合わせが最適」という意味)
上の表で「Aの平均」だけ見ると、A₁(51.5)> A₂(50.0)なのでA₁が良さそう。
「Bの平均」だけ見ると、B₂(53.0)> B₁(48.5)なのでB₂が良さそう。
この場合、偶然「A₁B₂」が最適と一致しますが、交互作用が有意な場合は必ず二元表の各セルを見て判断してください。周辺平均だけで判断すると、A₂B₁のような意外な組み合わせが最適だった場合に見逃してしまいます。
【ケース2】交互作用が有意でない場合の水準選択
交互作用A×Bが有意でない(またはプーリングした)場合、AとBは「単独」で最適な水準を選びます。
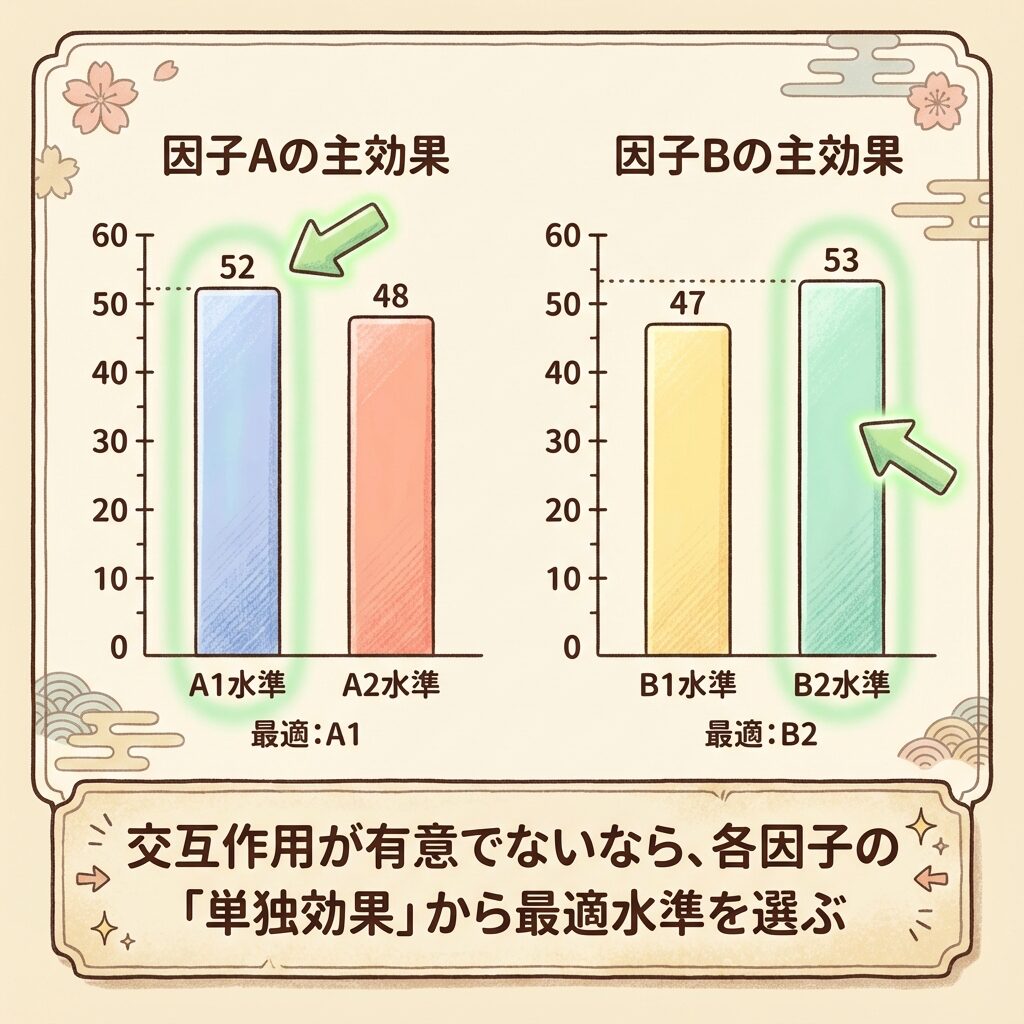
この場合は、各因子の主効果(水準ごとの平均)を比較して、それぞれ独立に最適水準を決めます。
手順:主効果から各因子の最適水準を選ぶ
因子A(2水準)と因子B(2水準)で実験を行った。
分散分析の結果、交互作用A×Bは有意でなかった。
目的:特性値を大きくしたい(望大特性)
Step 1:各因子の水準平均(主効果)を計算する
| A₁ | 54 ← 最大 |
| A₂ | 48 |
→ Aの最適水準:A₁
| B₁ | 46 |
| B₂ | 56 ← 最大 |
→ Bの最適水準:B₂
交互作用A×Bが有意でないので、最適水準は「Aの最適はA₁」「Bの最適はB₂」と別々に表現する。
結果として「A₁かつB₂」を採用することになりますが、これは「A₁B₂という組み合わせ」ではなく、「A₁とB₂をそれぞれ独立に選んだ結果」という意味です。
【実践】3因子以上の場合の水準選択
因子が3つ以上ある場合も、同じルールを適用します。
① 交互作用を確認
- A×Bが有意 → AとBは組み合わせで選ぶ
- A×Cが有意でない → AとCは別々に選ぶ
- B×Cが有意でない → BとCは別々に選ぶ
② 最適水準を決定
- AとBは「二元表」を見て、最適な組み合わせ(例:A₁B₂)を選ぶ
- Cは「単独」で、主効果が最適な水準(例:C₁)を選ぶ
→ 最適水準の表現:「A₁B₂、C₁」
【Step 4】点推定値μ̂の計算|「総平均+効果の和」で理解する
最適水準が決まったら、次は「その水準で実験したら、どれくらいの値が得られるか?」を推定します。これが点推定値μ̂(ミューハット)です。
点推定値の基本的な考え方
点推定値の計算は、実は非常にシンプルな考え方に基づいています。
もう少し具体的に書くと:
T̄ = 総平均(全データの平均)
Ā₁ − T̄ = A₁水準の効果(A₁の平均 − 総平均)
B̄₂ − T̄ = B₂水準の効果(B₂の平均 − 総平均)
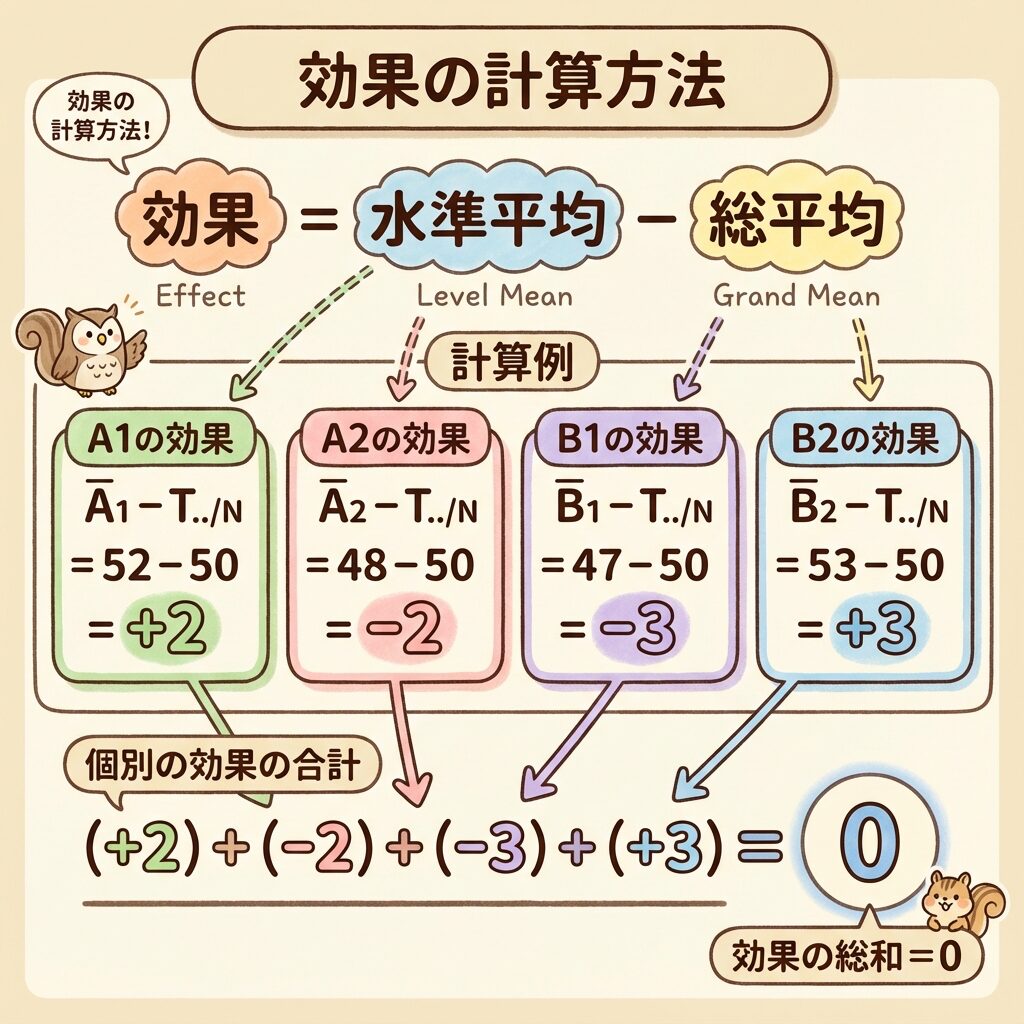
「効果」とは何か?
「効果」とは、その水準の平均値が、総平均からどれだけズレているかを表す値です。
例:総平均T̄ = 50のとき
- A₁の平均 = 54 → A₁の効果 = 54 − 50 = +4(総平均より4高い)
- A₂の平均 = 46 → A₂の効果 = 46 − 50 = −4(総平均より4低い)
- B₁の平均 = 48 → B₁の効果 = 48 − 50 = −2
- B₂の平均 = 52 → B₂の効果 = 52 − 50 = +2
点推定値は、この「効果」を積み上げていく計算です。
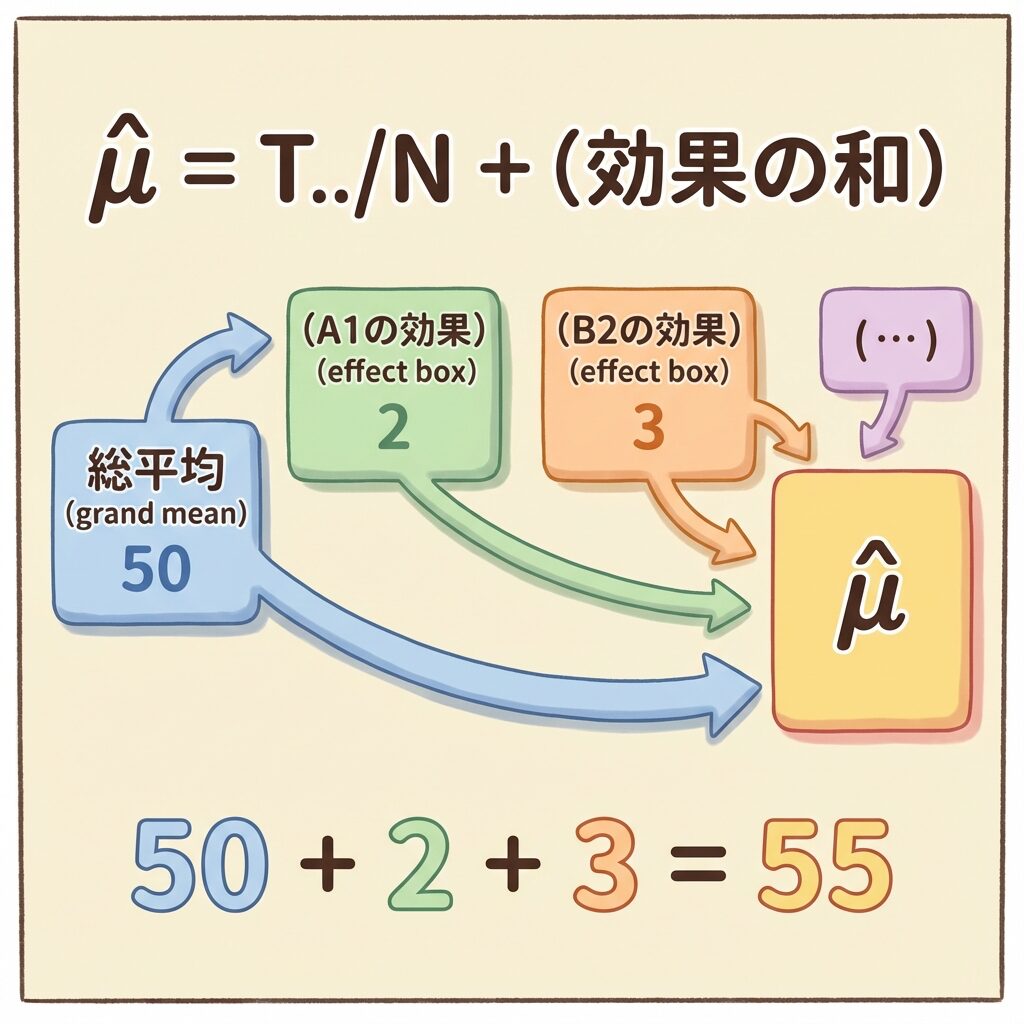
点推定値の計算は、「基準点(総平均)から、各因子の効果分だけズラす」というイメージです。
総平均50を出発点として...
→ A₁を選ぶと+4される
→ B₂を選ぶとさらに+2される
→ 結果:50 + 4 + 2 = 56
【ケース別】点推定値の計算公式
点推定値の公式は、交互作用が有意かどうかで変わります。これは最適水準の選び方と連動しています。
ケース1:交互作用が有意でない場合
各因子の効果を単純に足し合わせます。
これを整理すると:
T̄ = 50、Ā₁ = 54、B̄₂ = 52 のとき、最適水準A₁B₂の点推定値は?
μ̂ = Ā₁ + B̄₂ − T̄
= 54 + 52 − 50
= 56
ケース2:交互作用が有意な場合
交互作用が有意な場合、組み合わせの平均値をそのまま使うか、交互作用の効果も加える必要があります。
最もシンプルな方法は、その組み合わせの平均値をそのまま使うこと:
効果を分解して計算する方法(QC検定で出題されることがある):
交互作用効果 = (A₁B₂の平均) − Ā₁ − B̄₂ + T̄
交互作用が有意な場合、方法1(組み合わせの平均値をそのまま使う)が最も確実です。方法2は計算が複雑になるため、間違いやすいです。ただし、試験問題で「効果を分解して計算せよ」と指定されている場合は方法2を使います。
【応用】3因子以上の場合の点推定
因子が3つ以上ある場合も、基本的な考え方は同じです。有意な因子・交互作用の効果だけを加算します。
因子A, B, Cがあり、A×Bが有意、Cは単独で有意、A×C, B×Cは有意でない場合:
最適水準:A₁B₂、C₁
μ̂ = (A₁B₂の平均) + (C̄₁ − T̄)
※ A×Bは組み合わせの平均を使い、Cは単独の効果を加算
間違い1:有意でない因子の効果も加えてしまう
→ 有意でない因子は「効果がない(=0)」と見なすため、加算しません
間違い2:交互作用が有意なのに、因子を単独で扱う
→ A×Bが有意なら、AとBは必ず組み合わせで扱います
間違い3:総平均T̄を忘れる
→ 効果を足し合わせる場合、T̄を引く回数に注意(因子の数−1回引く)
【公式の導出】なぜこの計算になるのか?
点推定の公式がなぜこの形になるのか、少し深掘りしてみましょう。
実験計画法では、データを以下のようにモデル化します:
点推定では、誤差εを除いた「真の値」を推定します。
有意でない効果は「実質的にゼロ」と見なせるので、有意な効果だけを残して推定値を構成するのです。
【Step 5】分散の推定|有効繰返し数neがカギ
点推定値μ̂が求まったら、最後に「その推定値はどれくらいの精度か?」を評価します。
これが分散の推定であり、信頼区間の計算にも使われます。
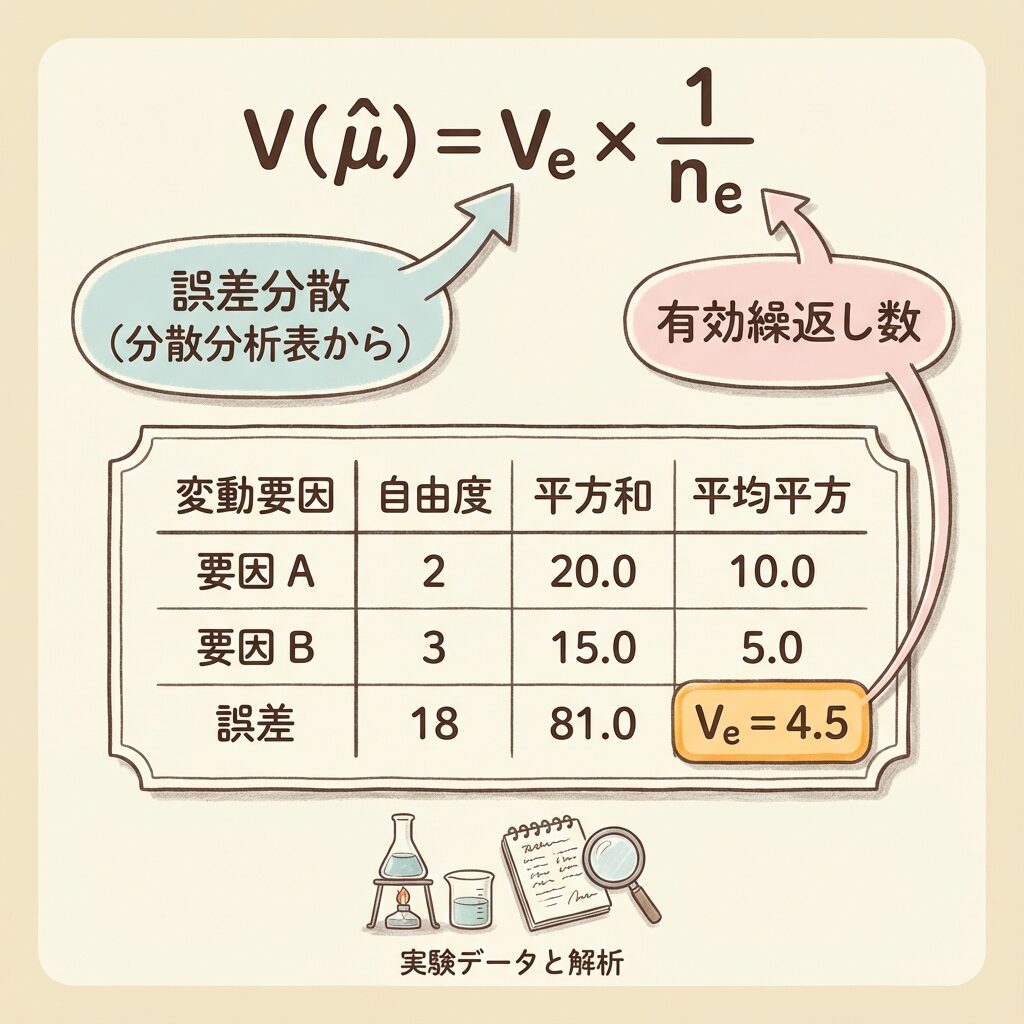
分散の推定公式
Ve:誤差分散(分散分析表のVeをそのまま使う)
ne:有効繰返し数(effective replication)
Veは分散分析表から読み取るだけなので簡単ですが、問題はne(有効繰返し数)です。これが分散推定で最もつまずきやすいポイントです。
有効繰返し数neとは何か?
有効繰返し数neとは、「点推定値を構成するのに、実質的に何回分のデータが使われているか」を表す値です。
たとえば、全部で12個のデータがあるとします。
- 総平均T̄を計算する場合 → 12個全部使う → n = 12
- A₁の平均Ā₁を計算する場合 → A₁に属する6個だけ使う → n = 6
- A₁B₂の平均を計算する場合 → A₁B₂に属する3個だけ使う → n = 3
点推定値μ̂は、これらの平均値を組み合わせて計算します。
その「組み合わせ方」によって、実質的なデータ数(ne)が変わるのです。
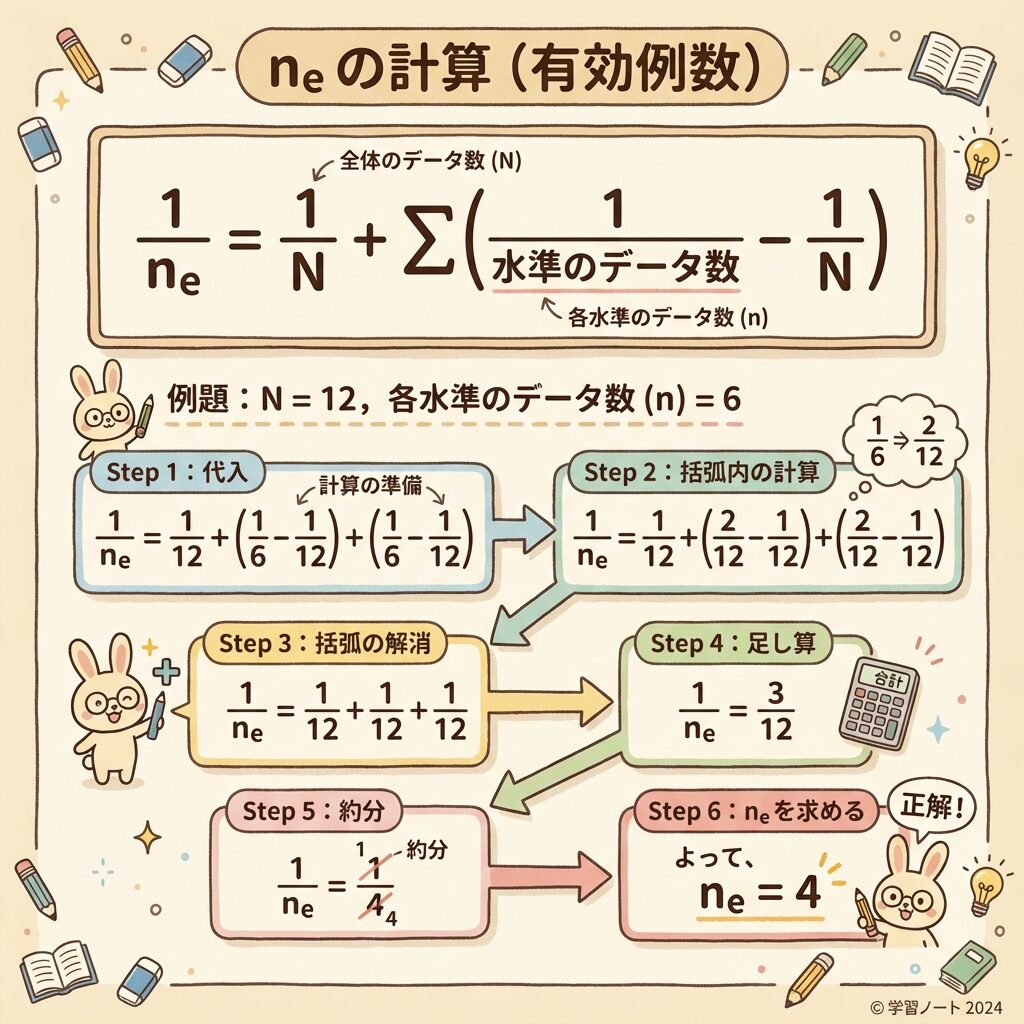
有効繰返し数neの計算公式
N:総データ数
n効果:その効果を計算するのに使ったデータ数
この公式は複雑に見えますが、「点推定値に含めた効果の数だけ、(1/n効果 − 1/N)を足す」というルールです。
有効繰返し数とは?実験回数の最適解を導く考え方|一元配置実験⑪ →
【計算例】有効繰返し数neを実際に求める
2因子実験(A: 2水準、B: 2水準、繰返し3回)を行った。
総データ数 N = 2 × 2 × 3 = 12
交互作用A×Bは有意でなく、最適水準はA₁とB₂(単独選択)。
点推定値 μ̂ = Ā₁ + B̄₂ − T̄ のときの有効繰返し数neを求めよ。
解答
Step 1:各効果のデータ数を確認
- 総平均T̄:N = 12個で計算
- Ā₁(A₁の平均):nA = 2 × 3 = 6個で計算
- B̄₂(B₂の平均):nB = 2 × 3 = 6個で計算
Step 2:公式に代入
1/ne = 1/N + (1/nA − 1/N) + (1/nB − 1/N)
= 1/12 + (1/6 − 1/12) + (1/6 − 1/12)
= 1/12 + 1/12 + 1/12
= 3/12 = 1/4
Step 3:neを求める
ne = 4 ← 1/(1/4) = 4
1/N を「基準」として考えると計算がラクです。
上の例では:
・基準の 1/N = 1/12
・A₁の効果を加えると +1/12 増える(= 1/6 − 1/12)
・B₂の効果を加えると +1/12 増える(= 1/6 − 1/12)
・合計:1/12 × 3 = 1/4 → ne = 4
別解:もっと簡単な公式
実は、よく使われる場合にはもっと簡単な公式があります。
上の例では:
・Aの効果の自由度 = 2−1 = 1
・Bの効果の自由度 = 2−1 = 1
・ne = 12 / (1 + 1 + 1) = 12 / 3 = 4
信頼区間の計算|点推定値の「確からしさ」を示す
点推定値μ̂と分散V(μ̂)が求まれば、信頼区間を計算できます。
信頼区間は、「最適水準での真の値は、95%の確率でこの範囲に入る」という情報を与えてくれます。
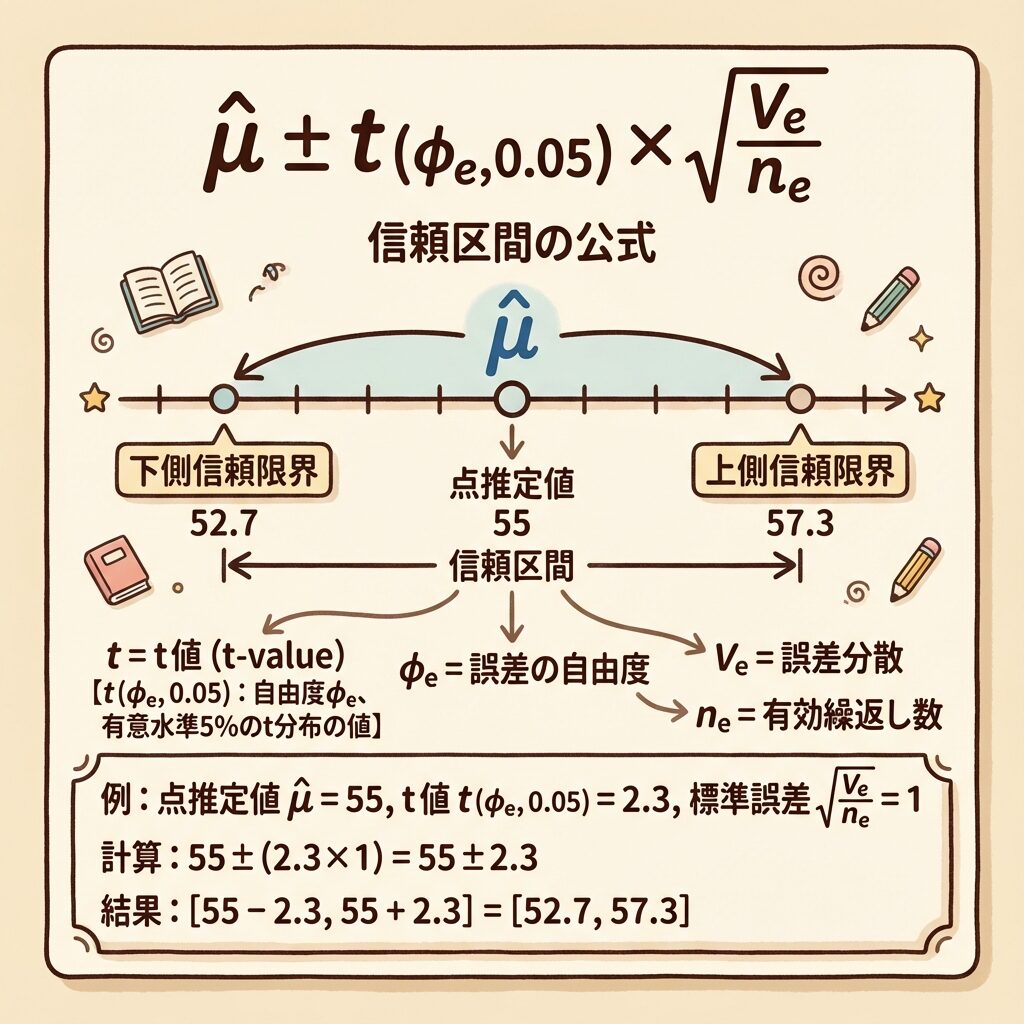
信頼区間の公式
μ̂:点推定値
t(φe, 0.05):t分布の上側2.5%点(両側5%)、自由度はφe
V(μ̂):点推定値の分散(= Ve/ne)
φe:誤差の自由度(分散分析表から)
【総合例題】最適水準から信頼区間まで一気に計算
2因子実験(A: 2水準、B: 2水準、繰返し3回、N=12)を行い、以下の結果を得た。
最適水準での母平均の95%信頼区間を求めよ。
与えられた情報:
・総平均 T̄ = 50
・Ā₁ = 54、Ā₂ = 46
・B̄₁ = 48、B̄₂ = 52
・交互作用A×Bは有意でない
・誤差分散 Ve = 8、誤差の自由度 φe = 8
・t(8, 0.05) = 2.306
・目的:特性値を大きくしたい
解答
【Step 1】最適水準を決定
交互作用が有意でないので、各因子を単独で選ぶ。
Aの最適:Ā₁ = 54 > Ā₂ = 46 → A₁
Bの最適:B̄₂ = 52 > B̄₁ = 48 → B₂
→ 最適水準:A₁、B₂
【Step 2】点推定値μ̂を計算
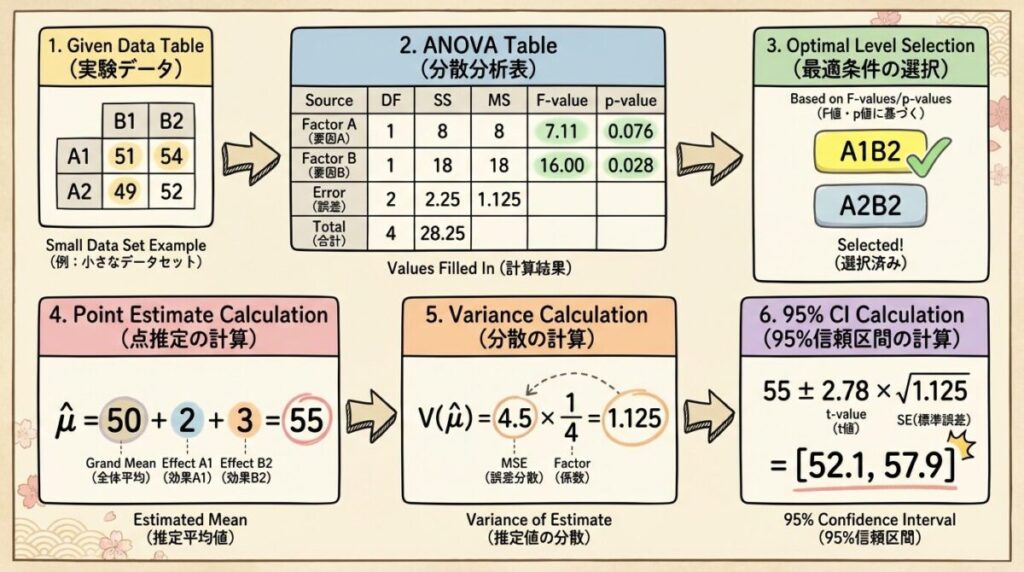
μ̂ = Ā₁ + B̄₂ − T̄ = 54 + 52 − 50 = 56
【Step 3】有効繰返し数neを計算
ne = N / (1 + φA + φB) = 12 / (1 + 1 + 1) = 4
【Step 4】分散V(μ̂)を計算
V(μ̂) = Ve / ne = 8 / 4 = 2
【Step 5】信頼区間を計算
信頼区間の幅 = t(8, 0.05) × √V(μ̂) = 2.306 × √2 = 2.306 × 1.414 = 3.26
95%信頼区間:56 − 3.26 ≦ μ ≦ 56 + 3.26
→ 52.74 ≦ μ ≦ 59.26
最適水準A₁B₂で実験を行うと、特性値は約56が期待でき、95%の確率で52.74〜59.26の範囲に収まると推定されます。
【まとめ】分散分析後の計算チェックリスト
最後に、この記事で解説した内容をチェックリスト形式でまとめます。
分散分析表でA×Bが有意かどうかを確認。これで水準の選び方が決まる。
・交互作用が有意 → 二元表から組み合わせで選ぶ
・交互作用が有意でない → 各因子を単独で選ぶ
・交互作用が有意 → 組み合わせの平均値を使う
・交互作用が有意でない → μ̂ = Ā₁ + B̄₂ − T̄ のように効果を足す
ne = N / (1 + 点推定に使った効果の自由度の合計)
V(μ̂) = Ve / ne
μ̂ ± t(φe, 0.05) × √V(μ̂)
実験計画法の「分散分析後の計算」は、公式を丸暗記するのではなく、「なぜその計算をするのか」を理解することが大切です。
・最適水準 → 「どの条件が最も良い結果を出すか」を知るため
・点推定 → 「その条件でどれくらいの値が出るか」を予測するため
・分散・信頼区間 → 「その予測はどれくらい信頼できるか」を評価するため
この「目的」を意識しながら計算すると、公式の意味がつながってきます。
📚 次に読むべき記事
一元配置実験の計算を基礎から復習したい方へ
二元配置実験の計算を詳しく学びたい方へ
直交表を使った実験の計算を学びたい方へ
実験計画法の全体像を把握したい方へ
【保存版】公式早見表
試験直前の確認用に、この記事で使った公式を一覧でまとめます。
点推定値 μ̂
| 交互作用が有意でない | μ̂ = Ā₁ + B̄₂ − T̄ (効果を足し合わせる) |
| 交互作用が有意 | μ̂ = (A₁B₂の平均値) (組み合わせの平均をそのまま使う) |
有効繰返し数 ne
| 簡易公式 | ne = N / (1 + 点推定に使った効果の自由度の合計) |
| 一般公式 | 1/ne = 1/N + Σ(1/n効果 − 1/N) |
分散・信頼区間
| 分散 | V(μ̂) = Ve / ne |
| 95%信頼区間 | μ̂ ± t(φe, 0.05) × √V(μ̂) |
この記事をブックマークしておくと、実験計画法の問題を解くときに「公式を忘れた!」という場面で役立ちます。