📖 この記事で解決できる悩み
- 「並列抵抗の公式、なぜ逆数なの?暗記できない...」
- 「ブリッジ回路や梯子回路が出てくると手が止まる」
- 「試験時間内に計算が終わらない!時短テクニックが知りたい」
- 「複雑な回路を見ると、どこから手をつけていいかわからない」
✅ この記事を読むとわかること
✔️ 直列・並列抵抗の基本と計算方法(暗記不要で理解できる!)
✔️ 並列抵抗の公式を「導出」から理解する方法
✔️ ブリッジ回路・梯子回路の攻略法(平衡判定・Y-Δ変換)
✔️ 試験で差がつく!時短計算テクニック4選
✔️ 電験三種で頻出する複雑回路の解き方
電験三種の理論科目で、「合成抵抗の計算」は避けて通れない超重要テーマです。しかし、多くの受験生が「並列抵抗の公式が覚えられない」「ブリッジ回路が出ると手が止まる」という悩みを抱えています。
実は、合成抵抗の計算は「暗記」ではなく「理解」で攻略できます。公式の導出過程を知れば、試験中に公式を忘れても自分で導けるようになります。また、ブリッジ回路や梯子回路も、基本パターンを押さえれば一発で解けるようになります。
この記事では、初心者でも理解できる図解と実例を使って、合成抵抗の計算テクニックを徹底解説します。読み終わる頃には、「複雑な回路も怖くない!」と自信を持てるようになりますよ。
⚠️ この記事を読む前に押さえておきたいポイント
- 直列は足し算、並列は逆数の和(この違いを体で覚える)
- 公式は暗記ではなく導出で理解(忘れても試験中に導ける)
- 複雑回路は基本パターンの組み合わせ(冷静に分解すればOK)
目次
1. 直列抵抗の計算|単純に足し算でOK!
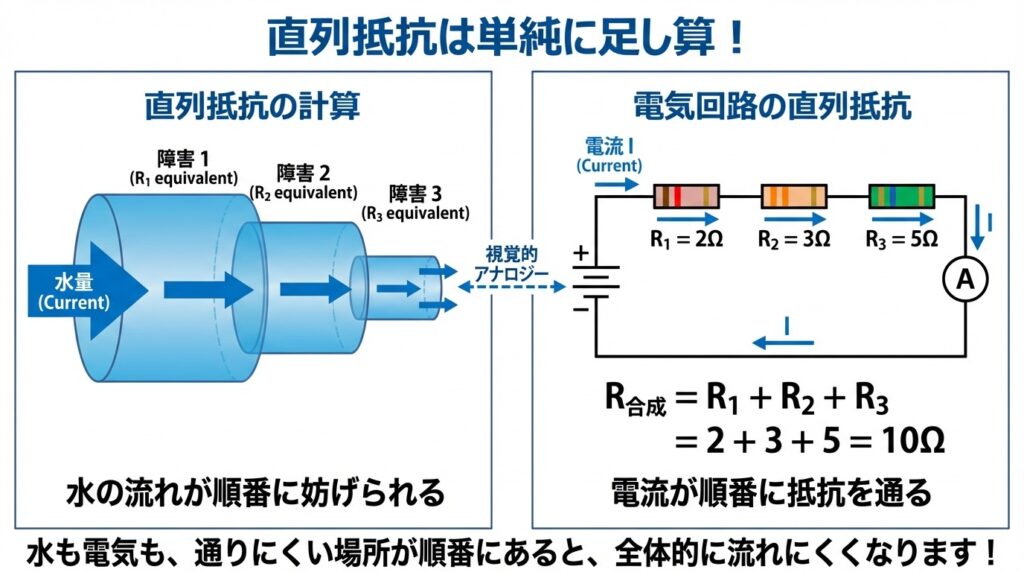
まずは最もシンプルな直列抵抗から見ていきましょう。直列抵抗は、抵抗が一列に並んでいる回路のことです。
💡 直列抵抗の公式
R合成 = R1 + R2 + R3 + ...
抵抗が一列に並んでいる場合は、単純に足し算すればOK!
🔍 なぜ足し算になるのか?
直列抵抗が足し算になる理由を、「水の流れ」で例えてみましょう。
| イメージ | 説明 |
|---|---|
| 水の流れ | 1本の水道管の中に、3つの障害物(狭い部分)がある |
| 電気回路 | 1つの経路に、3つの抵抗が順番に並んでいる |
| 結果 | 障害物(抵抗)が増えるほど、流れにくくなる → 抵抗値は足し算 |
📝 例題
R1 = 2Ω、R2 = 3Ω、R3 = 5Ω の抵抗が直列に接続されています。合成抵抗を求めてください。
✅ 答え: R合成 = 2 + 3 + 5 = 10Ω
直列抵抗は、考え方さえ理解すれば小学生でも解けるレベルの計算です。問題は次の「並列抵抗」です。

2. 並列抵抗の計算|公式を暗記不要で導く方法
多くの受験生が苦手とする並列抵抗。公式を丸暗記しようとして挫折していませんか?
💡 並列抵抗の公式
1/R合成 = 1/R1 + 1/R2 + 1/R3 + ...
並列抵抗は「逆数の和」で計算する
🔬 公式を導出してみよう(暗記不要!)
「なぜ逆数なの?」という疑問を解消するために、オームの法則から導出してみましょう。
📐 導出ステップ
ステップ1: 並列回路では、各抵抗に同じ電圧Vがかかる
オームの法則より: I1 = V/R1、I2 = V/R2、I3 = V/R3
ステップ2: 全体の電流は各枝の電流の合計
I = I1 + I2 + I3 = V/R1 + V/R2 + V/R3
ステップ3: 合成抵抗R合成を使うと
V = I × R合成 なので I = V/R合成
ステップ4: 2つの式を等しいとおくと
V/R合成 = V/R1 + V/R2 + V/R3
ステップ5: 両辺をVで割ると
1/R合成 = 1/R1 + 1/R2 + 1/R3
📝 例題
R1 = 6Ω、R2 = 3Ω、R3 = 2Ω の抵抗が並列に接続されています。合成抵抗を求めてください。
✅ 解答:
1/R = 1/6 + 1/3 + 1/2
= 1/6 + 2/6 + 3/6
= 6/6 = 1
∴ R合成 = 1Ω
💡 重要ポイント
並列抵抗の合成抵抗は、「最も小さい抵抗値よりもさらに小さくなる」という特徴があります。上の例では、最小の抵抗が2Ωなのに、合成抵抗は1Ωになっていますよね。
3. 時短計算テクニック|試験で差がつく4つの裏ワザ
並列抵抗の計算は、工夫次第で劇的に時短できます。試験会場で差がつく4つのテクニックを紹介します。
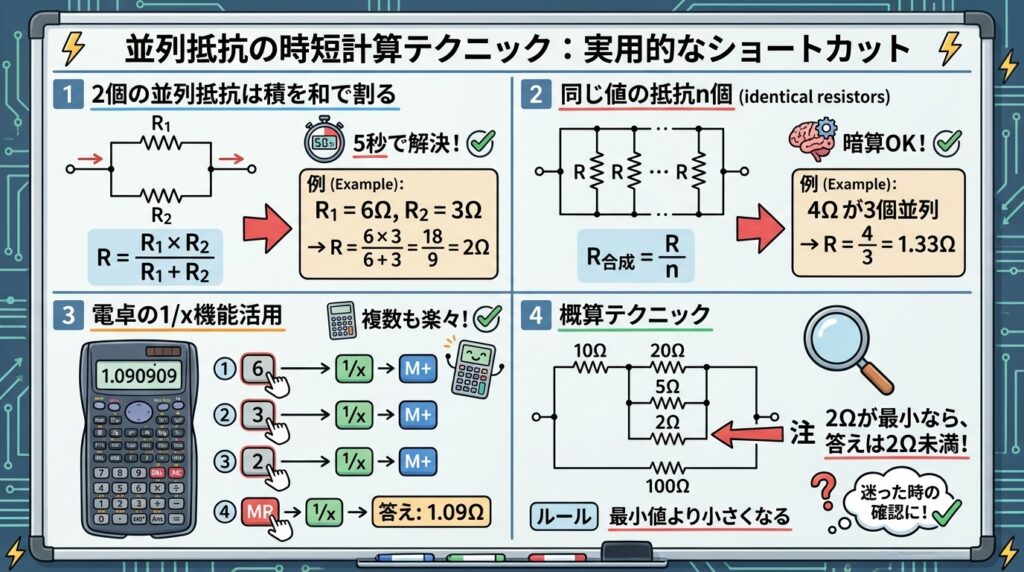
⚡ テクニック1: 2個の並列抵抗は「積を和で割る」
R = (R1 × R2) / (R1 + R2)
2つだけなら、逆数計算より速い!
📝 例題
R1 = 6Ω、R2 = 3Ω の並列抵抗を求めてください。
✅ 解答: R = (6 × 3) / (6 + 3) = 18 / 9 = 2Ω
⏱️ 所要時間: 約5秒!
⚡ テクニック2: 同じ値の抵抗n個は「R/n」
R合成 = R / n
同じ値の抵抗が複数個なら、割り算だけでOK!
📝 例題
4Ωの抵抗が3個並列に接続されています。合成抵抗を求めてください。
✅ 解答: R = 4 / 3 = 1.33Ω
⏱️ 所要時間: 暗算OK!
⚡ テクニック3: 電卓の「1/x」機能を活用
3個以上の並列抵抗を計算するときは、電卓のメモリー機能(M+)と逆数ボタン(1/x)を使うと爆速です。
🧮 電卓操作手順
- 6 → 1/x → M+ (0.1666...をメモリーに追加)
- 3 → 1/x → M+ (0.3333...をメモリーに追加)
- 2 → 1/x → M+ (0.5をメモリーに追加)
- MR → 1/x → 答え: 1.09Ω
⏱️ 所要時間: 約10秒で複数の並列抵抗も楽々!
⚡ テクニック4: 概算テクニック(検算に使える)
💡 覚えておきたいルール
並列抵抗の合成抵抗は、「最小の抵抗値より必ず小さくなる」という性質があります。
例: 2Ω、3Ω、6Ωの並列回路なら、答えは「2Ω未満」と予測できます。
もし計算結果が2Ω以上になったら、計算ミスです!
✅ 時短テクニックまとめ
| 状況 | 使うテクニック | 所要時間 |
|---|---|---|
| 2個の並列抵抗 | 積を和で割る | 約5秒 |
| 同じ値n個 | R/n | 暗算OK |
| 3個以上 | 電卓の1/x+M+ | 約10秒 |
| 検算 | 最小値より小さいかチェック | 即座 |
4. ブリッジ回路の攻略法|3ステップで解く
電験三種で頻出するブリッジ回路。複雑に見えますが、平衡判定さえマスターすれば一発で解けます。
🔍 ブリッジ回路とは?
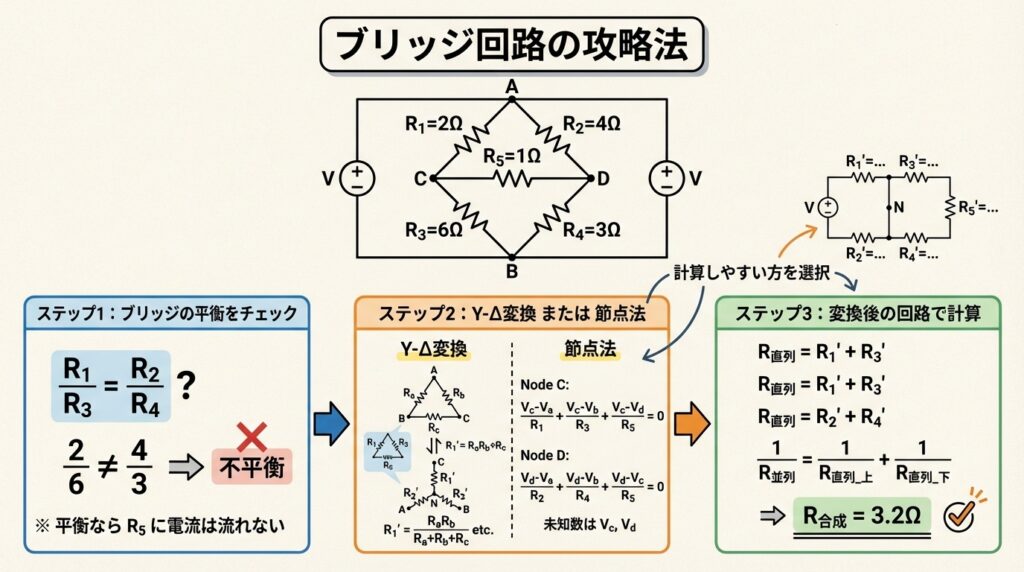
ブリッジ回路とは、5つの抵抗がひし形(ブリッジ)状に配置された回路のことです。中央の抵抗R5が「ブリッジ」の役割を果たしています。
⚡ ステップ1: ブリッジの平衡をチェック
R1 / R3 = R2 / R4 ならば「平衡ブリッジ」
平衡している場合、R5には電流が流れない!
📝 例題
R1 = 2Ω、R2 = 4Ω、R3 = 6Ω、R4 = 3Ω、R5 = 1Ω のブリッジ回路があります。平衡していますか?
✅ 解答:
R1/R3 = 2/6 = 1/3
R2/R4 = 4/3
1/3 ≠ 4/3 なので 不平衡
⚡ ステップ2: Y-Δ変換 または 節点法を使う
不平衡ブリッジの場合、以下の2つの方法があります:
| 方法 | 難易度 | 特徴 |
|---|---|---|
| Y-Δ変換 | ★★★☆☆ | 回路を変形して直列・並列の基本形に戻す |
| 節点法 | ★★★★☆ | 連立方程式を立てて解く(計算量多い) |
💡 電験三種の裏ワザ
実は電験三種では、「平衡ブリッジ」が出題されることが多いです。平衡していればR5を無視できるので、計算が一気に楽になります!
⚡ ステップ3: 変換後の回路で計算
変換後は、直列・並列の基本パターンに戻るので、これまで学んだテクニックで一発です。
5. 梯子回路の攻略法|右から順番に合成していく
もう1つの頻出パターン、梯子(はしご)回路。名前の通り、はしごのように抵抗が並んだ回路です。
🪜 梯子回路とは?
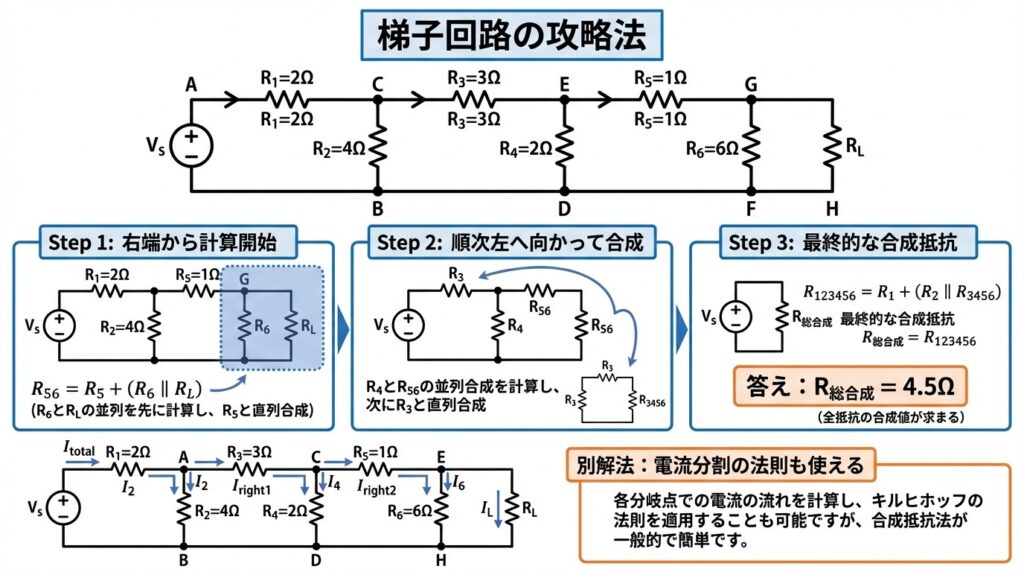
梯子回路は、横方向の抵抗と縦方向の抵抗が交互に繰り返される回路です。一見複雑ですが、右端から順番に合成していけば必ず解けます。
⚡ 攻略ステップ
📐 解き方の流れ
ステップ1: 右端から計算開始
最も右側のセクション(R5とR6)を合成する
ステップ2: 順次左へ向かって合成
合成した抵抗を1つの抵抗と見なし、次のセクション(R4)と合成
これを繰り返す
ステップ3: 最終的な合成抵抗を求める
すべて合成し終わったら、それが答え!
⚠️ よくある失敗
「左から計算し始める」のはNG!左から始めると、後ろの影響を考慮できず計算が複雑になります。
必ず「右端から」計算を始めましょう。
💡 梯子回路の本質
梯子回路は、「複雑に見えても、実は直列・並列の組み合わせ」です。右から順番に分解していけば、必ず基本パターンに戻ります。
✅ 複雑回路攻略の黄金ルール
- ブリッジ回路 → 平衡判定してからY-Δ変換
- 梯子回路 → 右端から順番に合成
- それ以外 → 直列・並列の基本に分解
6. まとめ|合成抵抗の計算で差をつける
合成抵抗の計算は、「暗記」ではなく「理解」が鍵です。この記事で紹介したテクニックを使えば、試験本番でも自信を持って解けるようになります。
📚 今日覚えた重要ポイント
| 回路の種類 | 計算方法 | 時短テクニック |
|---|---|---|
| 直列抵抗 | R = R1 + R2 + R3... | 単純に足し算 |
| 並列抵抗(2個) | R = (R1×R2)/(R1+R2) | 積を和で割る |
| 並列抵抗(同じ値n個) | R = R/n | 割り算だけ |
| 並列抵抗(3個以上) | 1/R = 1/R1 + 1/R2... | 電卓の1/x+M+ |
| ブリッジ回路 | 平衡判定 → Y-Δ変換 | 平衡ならR5無視 |
| 梯子回路 | 右端から順番に合成 | 右→左の流れ |
🚀 次に読むべき記事
合成抵抗の計算をマスターしたら、次はキルヒホッフの法則で複雑な回路の電流・電圧を求める方法を学びましょう。
👉 キルヒホッフの法則|第1法則と第2法則の違いを実例で完全理解
また、複雑な回路を一発で簡単にするテブナンの定理も必見です。
👉 テブナンの定理|複雑な回路を一発で簡単にする魔法の定理
💪 最後に: 合格への道は「理解」の積み重ね
電験三種の理論科目は、公式を暗記するのではなく、なぜそうなるのか?を理解することが合格への最短ルートです。
今日学んだ「合成抵抗の計算」は、回路理論の基礎中の基礎。ここをしっかり固めれば、これから学ぶすべての単元が理解しやすくなります。
あなたなら絶対にできます。一緒に合格を目指しましょう!
📖 電験三種の理論科目、一緒に攻略しましょう!
次の記事でお会いしましょう 😊
