💡 この記事でわかること
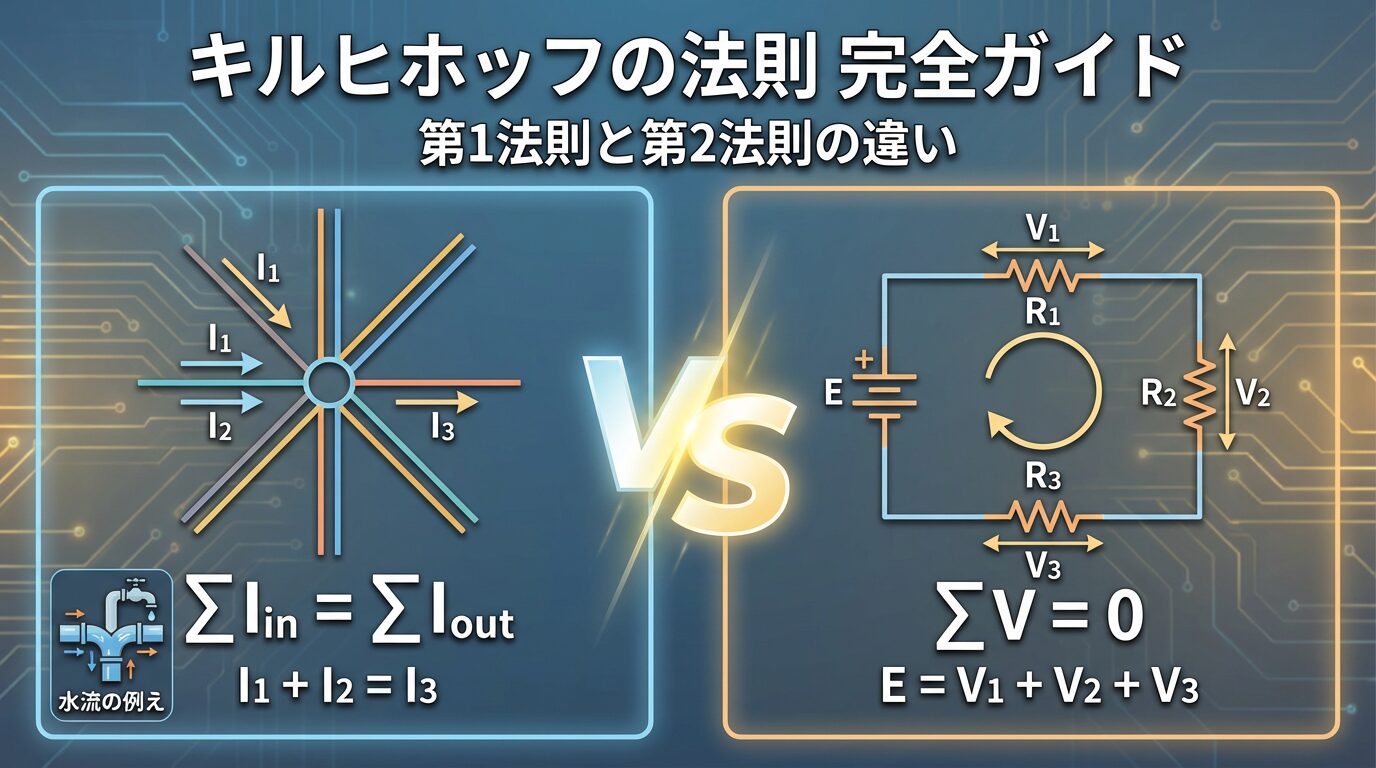
キルヒホッフの法則は、複雑な回路を解析するための2つの基本法則です。
第1法則(電流則)は「接続点に流入する電流の和=流出する電流の和」、第2法則(電圧則)は「閉回路の電圧降下の総和=起電力」を表します。
この記事では、初心者でも絶対に理解できるように、2つの法則の違いから実際の計算方法まで、合格に必要な内容に絞って丁寧に解説します!
⚡ こんな疑問を持っていませんか?
- 第1法則と第2法則の違いが曖昧…
- 「電流保存の法則」って何?
- 「電圧降下の総和」の意味がわからない
- 実際の問題でどう使い分けるの?
目次
1️⃣ キルヒホッフの法則とは?
🔍 2つの法則の全体像
キルヒホッフの法則は、ドイツの物理学者グスタフ・キルヒホッフが発見した、複雑な回路を解析するための2つの基本原理です。
📚 2つの法則:
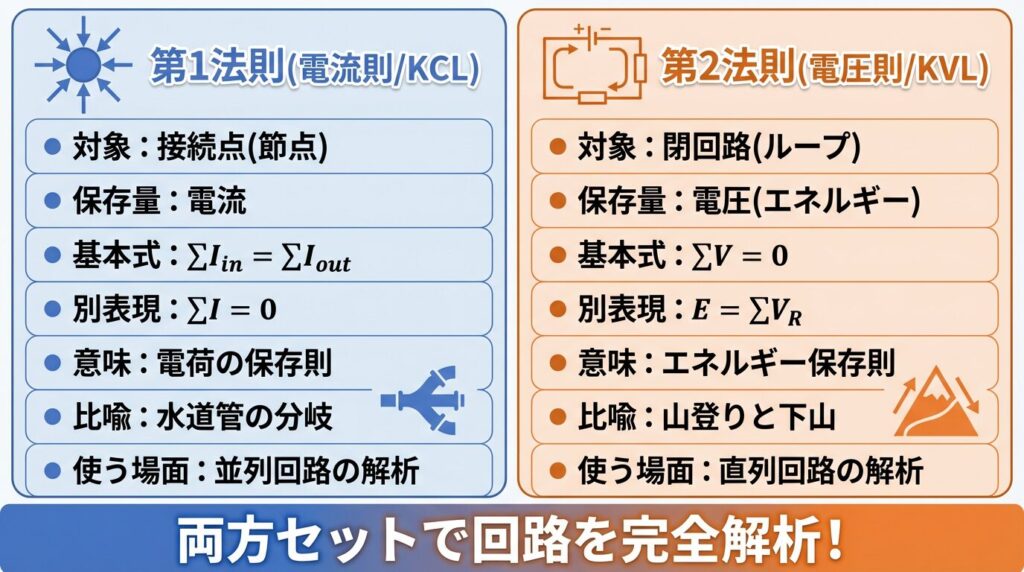
• 第1法則(電流則/KCL): 接続点での電流保存
• 第2法則(電圧則/KVL): 閉回路でのエネルギー保存
🎯 重要性: オームの法則だけでは解けない複雑な回路を解析できる!
📐 いつ使うの?
単純な回路:
• 抵抗が直列または並列だけ → オームの法則でOK
複雑な回路:
• 抵抗が複雑に接続されている
• 複数の電源がある
• ブリッジ回路など
→ キルヒホッフの法則が必須!
🔗 関連記事:
📖 電験三種「理論」科目攻略法
📖 電験三種の公式暗記術
📖 統計の基礎知識
2️⃣ 第1法則(電流則)│電流保存の法則
💧 水道管で理解しよう!
第1法則の本質:
「接続点(節点)に流れ込む電流の合計 = 流れ出る電流の合計」
💡 水道管の比喩:
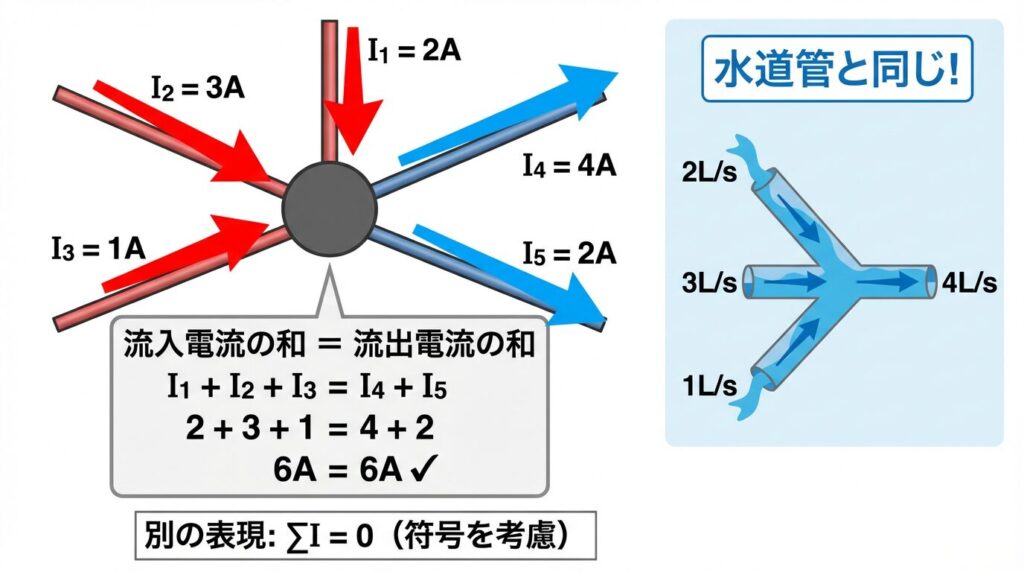
水道管が分岐するとき、流入する水の量 = 流出する水の量ですよね?電流も同じです!
別の表現:
流入を+(プラス)、流出を-(マイナス)とすれば:
🧮 具体例で理解する
【例】ある接続点Aに:
• 流入する電流: I₁ = 2A、I₂ = 3A、I₃ = 1A
• 流出する電流: I₄ = ?A、I₅ = 2A
第1法則を適用:
流入の合計 = 流出の合計
I₁ + I₂ + I₃ = I₄ + I₅
2 + 3 + 1 = I₄ + 2
6 = I₄ + 2
🎯 第1法則のポイント
✅ 覚えるべきこと:
• 対象: 接続点(節点)
• 保存されるもの: 電流(電荷)
• 物理的意味: 電荷保存則
• 使う場面: 並列回路や複雑な分岐点
💡 電流の向きは最初に仮定すればOK!負の値が出たら逆向きの意味です。
🔗 関連記事:
📖 電験三種「理論」科目の計算問題攻略法
📖 YouTubeで電験三種を制する独学インプット法
📖 統計学の基礎│品質管理への応用
3️⃣ 第2法則(電圧則)│電圧降下の総和
⛰️ 山登りで理解しよう!
第2法則の本質:
「閉回路を一周したときの電圧の総和 = 0」
💡 山登りの比喩:
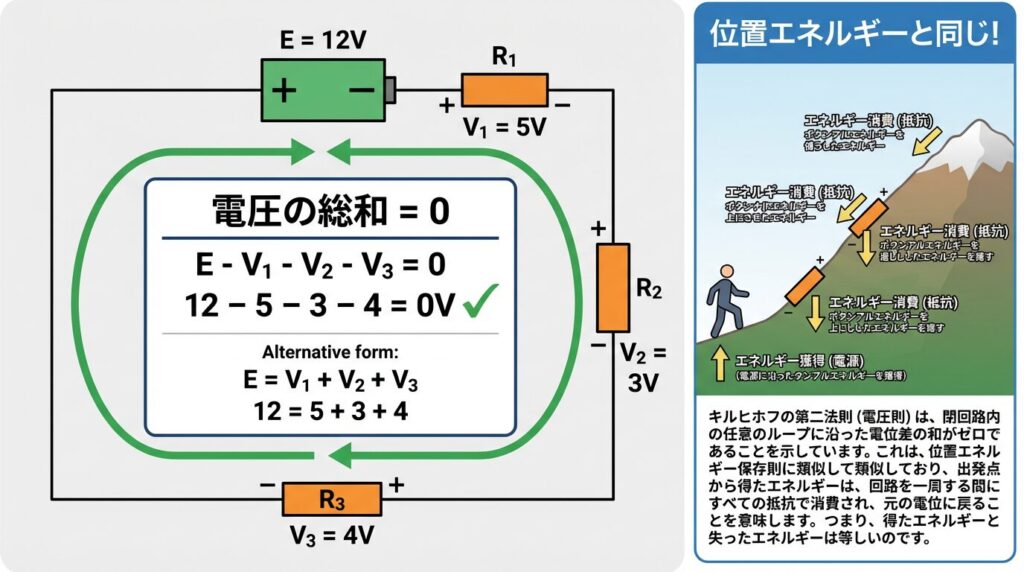
山を登って同じ場所に戻ってくると、位置エネルギーの変化はゼロですよね?電圧(電気的なエネルギー)も同じです!
実用的な表現:
起電力E = 各抵抗での電圧降下の合計
🧮 具体例で理解する
【例】単純な直列回路:
• 電池: E = 12V
• 抵抗R₁での電圧降下: V₁ = 5V
• 抵抗R₂での電圧降下: V₂ = 3V
• 抵抗R₃での電圧降下: V₃ = ?V
第2法則を適用:
E - V₁ - V₂ - V₃ = 0
(起電力は+、電圧降下は-)
12 - 5 - 3 - V₃ = 0
V₃ = 12 - 5 - 3
または:
E = V₁ + V₂ + V₃
12 = 5 + 3 + 4 ✓
🎯 第2法則のポイント
✅ 覚えるべきこと:
• 対象: 閉回路(ループ)
• 保存されるもの: 電圧(エネルギー)
• 物理的意味: エネルギー保存則
• 使う場面: 直列回路や複雑なループ
💡 符号のルール:ループの向きに進むとき、起電力は+、電圧降下は-!
⚠️ よくある間違い:
• 符号を間違える → ループの向きを決めて統一!
• 電圧降下の向きを逆にする → 電流の向きに注意!
• 複数のループで混乱 → 1つずつ丁寧に!
🔗 関連記事:
📖 電験三種「理論」科目の頻出計算問題
📖 電験三種の公式暗記術
📖 電験三種とは?資格の全体像
4️⃣ 第1法則と第2法則の比較
📊 徹底比較表
| 比較項目 | 第1法則(電流則) | 第2法則(電圧則) |
|---|---|---|
| 対象 | 接続点(節点) | 閉回路(ループ) |
| 保存量 | 電流(電荷) | 電圧(エネルギー) |
| 基本式 | ΣIin = ΣIout | ΣV = 0 |
| 別表現 | ΣI = 0 | E = ΣVR |
| 物理的意味 | 電荷保存則 | エネルギー保存則 |
| 比喩 | 水道管の分岐 | 山登りと下山 |
| 使う場面 | 並列回路の解析 | 直列回路の解析 |
🔄 使い分けのコツ
判断基準:
❓ 問題文に「接続点」「節点」が出てきたら?
→ 第1法則(電流則)を使う!
❓ 問題文に「ループ」「閉回路」が出てきたら?
→ 第2法則(電圧則)を使う!
❓ 複雑な回路で全体を解く場合は?
→ 両方組み合わせて連立方程式を作る!
💡 実際には両方セットで使うことが多いです!
🔗 関連記事:
📖 電験三種「電力」科目攻略
📖 電験三種「機械」科目攻略
📖 電験三種の合格率と難易度
5️⃣ 実践!両方使った計算例
📝 例題:複雑な回路の解析
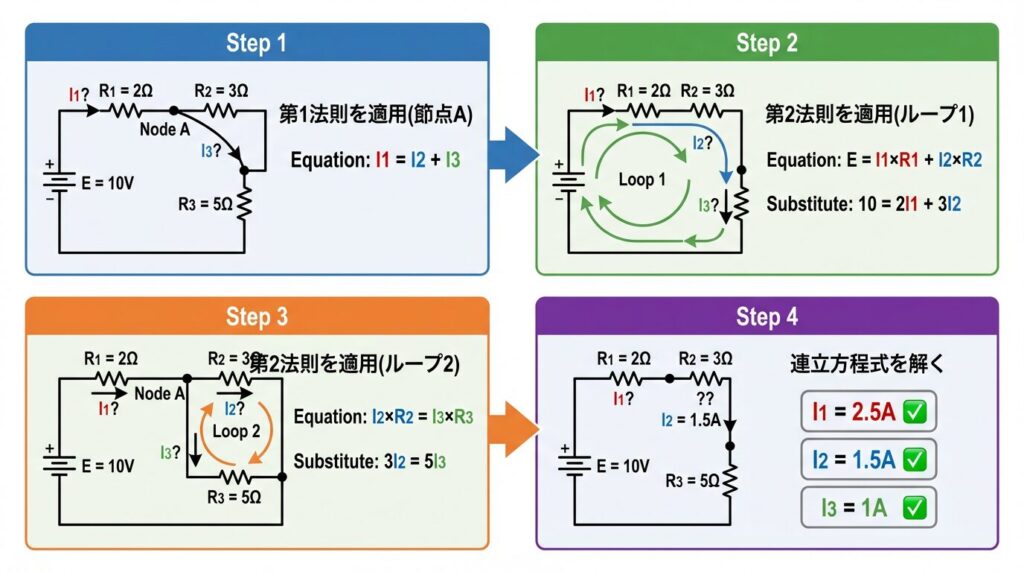
【問題】次の回路の電流I₁、I₂、I₃を求めよ
回路構成:
• 電池E = 10V
• 抵抗R₁ = 2Ω(I₁が流れる)
• 抵抗R₂ = 3Ω(I₂が流れる)
• 抵抗R₃ = 5Ω(I₃が流れる)
• 節点Aで電流が分岐
【解答ステップ】
ステップ1:第1法則を適用(節点A)
I₁ = I₂ + I₃ ... ①
ステップ2:第2法則を適用(ループ1)
E = I₁×R₁ + I₂×R₂
10 = 2I₁ + 3I₂ ... ②
ステップ3:第2法則を適用(ループ2)
I₂×R₂ = I₃×R₃
3I₂ = 5I₃
I₃ = 0.6I₂ ... ③
ステップ4:連立方程式を解く
①に③を代入:
I₁ = I₂ + 0.6I₂ = 1.6I₂
これを②に代入:
10 = 2(1.6I₂) + 3I₂
10 = 3.2I₂ + 3I₂
10 = 6.2I₂
I₂ = 1.61A
I₃ = 0.6 × 1.61 = 0.97A
I₁ = 1.6 × 1.61 = 2.58A
💡 解法のコツ
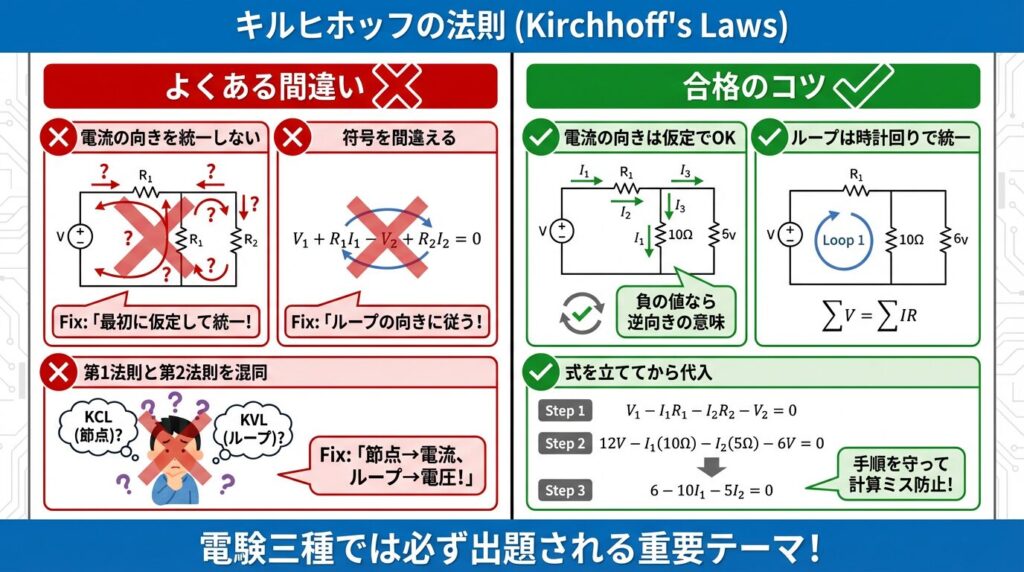
合格のための5つのポイント:
1. 電流の向きを仮定する
• 最初に全ての電流の向きを矢印で書く
• 間違っていてもOK!(負の値になるだけ)
2. ループの向きを統一する
• 時計回りに統一すると混乱しない
• 一度決めたら変えない!
3. 式を立ててから代入
• いきなり数値を入れない
• 文字式で立ててから最後に代入
4. 符号に注意
• 起電力:ループの向きに進むとき+
• 電圧降下:電流の向きに進むとき-
5. 検算を忘れずに
• 求めた電流を元の式に代入して確認!
🔗 関連記事:
📖 電験三種「理論」科目の完全攻略ガイド
📖 独学者のための電験三種試験対策
📖 電験三種の公式暗記術
6️⃣ よくある間違いと対策
⚠️ 間違いパターン集
❌ 間違い1:電流の向きを途中で変える
→ 最初に仮定した向きを最後まで使う!
❌ 間違い2:符号をテキトーにする
→ ループの向きを明確にして統一!
❌ 間違い3:第1法則と第2法則を混同
→ 節点なら電流、ループなら電圧!
❌ 間違い4:単位を間違える
→ mA→Aの変換に注意!
❌ 間違い5:連立方程式の計算ミス
→ 必ず検算する習慣を!
📝 電験三種での出題パターン
頻出問題タイプ:
1. 基礎問題:単純な直列・並列
「次の回路の電流Iを求めよ」
→ 第1法則または第2法則のどちらか1つで解ける
2. 標準問題:複雑な回路
「各枝の電流を全て求めよ」
→ 両方の法則を組み合わせて連立方程式
3. 応用問題:ブリッジ回路
「平衡条件を満たす抵抗値は?」
→ キルヒホッフの法則から導出
💡 理論科目では毎年必ず1~2問出題される超重要テーマ!
🔗 関連記事:
📖 電験三種「電力」科目攻略
📖 電験三種「機械」科目攻略
📖 電験三種の合格率と難易度
📚 まとめ│キルヒホッフの法則で合格する
🎯 この記事の重要ポイント
- 第1法則:接続点で電流保存(ΣIin=ΣIout)
- 第2法則:閉回路で電圧の総和ゼロ(ΣV=0)
- 第1法則は電荷保存則、第2法則はエネルギー保存則
- 複雑な回路は両方組み合わせて連立方程式を作る
- 電流の向きは仮定でOK(負なら逆向き)
- 電験三種では毎年必出の超重要テーマ!
💪 次のステップ
初心者のあなたへ:
まずは「節点→電流、ループ→電圧」という基本を覚えましょう!水道管と山登りの比喩で理解すると忘れません。
電験三種受験者のあなたへ:
過去問で「キルヒホッフの法則」を使う問題を5問解いてみましょう。両方の法則を組み合わせる練習が重要です!
さらに深く学びたいあなたへ:
ブリッジ回路やホイートストンブリッジなど、キルヒホッフの法則の応用問題にチャレンジしてみましょう!
🔗 あわせて読みたい関連記事
📖 電験三種「理論」科目の完全攻略ガイド
📖 独学者のための電験三種試験対策
📖 電験三種の公式暗記術
📖 電験三種とは?資格の全体像を解説
📖 30代未経験から電験三種で年収500万円を目指す方法
📖 統計学の基礎知識