目次
直列回路と並列回路、何が違うの?
電験三種の理論科目では、直列回路と並列回路の違いを理解することが、合格への第一歩です。回路の種類によって、電圧や電流の分配のルールがまったく異なります。
この記事では、「直列回路はまるで数珠つなぎ」「並列回路は道路の分岐のよう」という身近な例えを使って、初心者の方でも一瞬で理解できるよう丁寧に解説します。
特に、合成抵抗の公式は試験頻出です。直列回路では抵抗を足し算、並列回路では逆数を足してもう一度逆数に直すという、この2つのパターンをしっかりマスターしましょう。
直列回路とは?|数珠つなぎでつながる回路
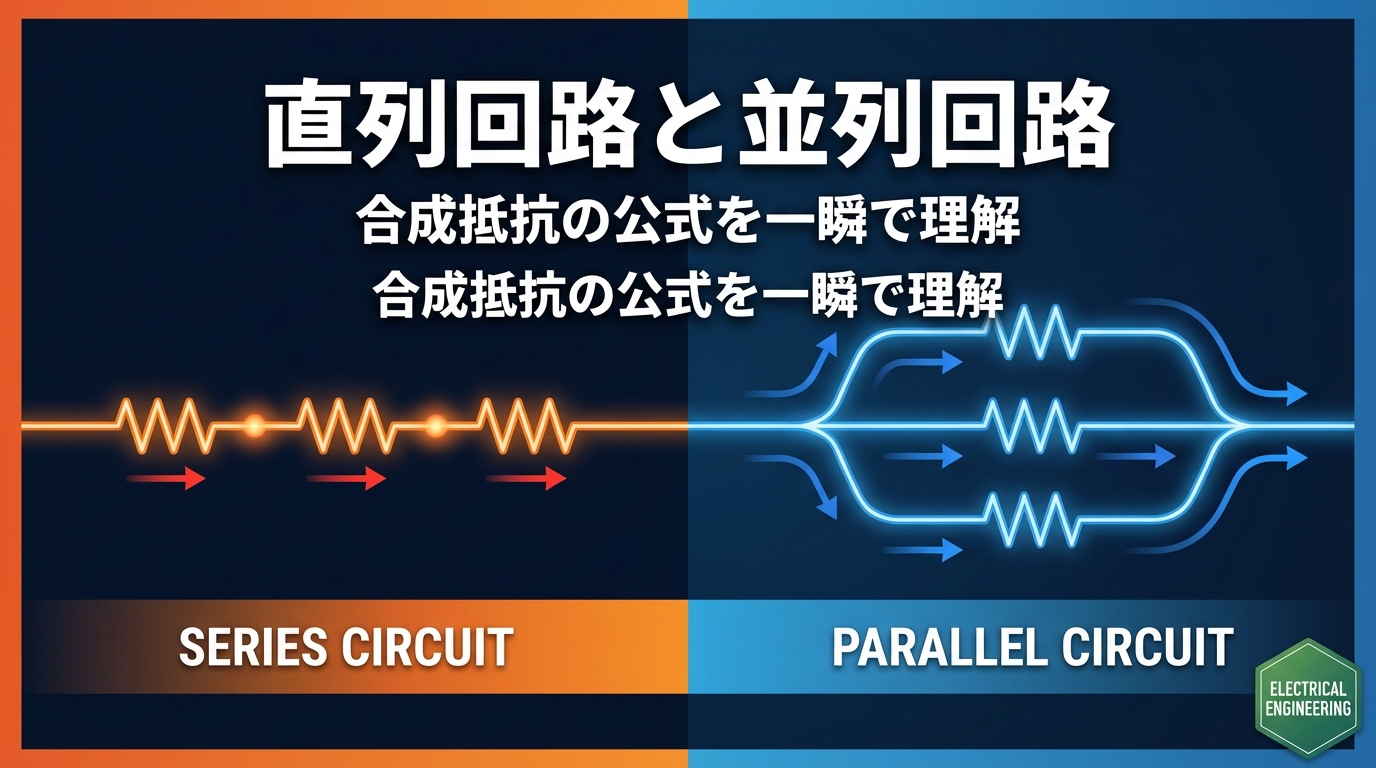
直列回路の基本構造
直列回路とは、抵抗などの部品が一直線に数珠つなぎで接続された回路のことです。電流が流れる道は一本だけで、すべての部品を順番に通過していきます。
イメージとしては、お念珠の玉が一本の糸でつながっているような状態です。電流はこの一本道を進むため、どの部品でも同じ大きさの電流が流れます。
直列回路の3つの特徴
直列回路には、次の3つの重要な特徴があります。
✅ 直列回路の3つの特徴
- ① 電流はどこでも同じ:I = I₁ = I₂ = I₃
- ② 電圧は分担される:V = V₁ + V₂ + V₃
- ③ 抵抗は合計される:R = R₁ + R₂ + R₃
一本道なので電流は変わりませんが、電圧はそれぞれの抵抗で分担されて消費されていきます。
直列回路の合成抵抗の公式
直列回路では、抵抗がつながるほど電流が流れにくくなります。そのため、合成抵抗(全体の抵抗)は各抵抗を足し算するだけで求められます。
📐 直列回路の合成抵抗の公式
R = R₁ + R₂ + R₃ + ... + Rₙ
すべての抵抗を足し算するだけ!
計算例:直列回路の合成抵抗
実際に計算してみましょう。3つの抵抗R₁=10Ω、R₂=20Ω、R₃=30Ωが直列に接続されている場合です。
💡 計算手順
R = R₁ + R₂ + R₃
R = 10Ω + 20Ω + 30Ω
R = 60Ω
このように、直列回路では単純な足し算で求められるため、計算がとても簡単です。
並列回路とは?|枝分かれでつながる回路
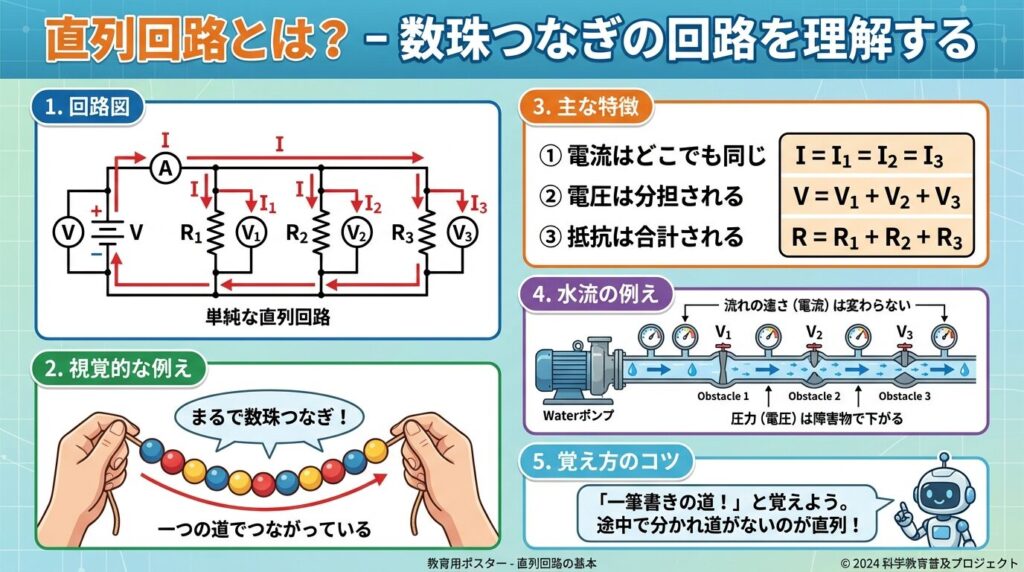
並列回路の基本構造
並列回路とは、抵抗などの部品が枝分かれして並んで接続された回路のことです。電流が流れる道が複数あり、電流は分岐して各部品に分かれて流れます。
イメージとしては、高速道路が複数の車線に分かれているような状態です。電流はそれぞれの道に分かれて流れるため、各部品に同じ電圧がかかります。
並列回路の3つの特徴
並列回路には、次の3つの重要な特徴があります。
✅ 並列回路の3つの特徴
- ① 電圧はどこでも同じ:V = V₁ = V₂ = V₃
- ② 電流は分担される:I = I₁ + I₂ + I₃
- ③ 抵抗の逆数を合計:1/R = 1/R₁ + 1/R₂ + 1/R₃
道が複数あるため電圧は同じですが、電流はそれぞれの抵抗に分かれて流れます。
並列回路の合成抵抗の公式
並列回路では、抵抗が増えるほど電流の通り道が増えるため、合成抵抗は元の抵抗よりも小さくなります。公式は少し複雑ですが、逆数を足してもう一度逆数にすると覚えましょう。
📐 並列回路の合成抵抗の公式
1/R = 1/R₁ + 1/R₂ + 1/R₃ + ... + 1/Rₙ
逆数を足し算してから、もう一度逆数にする!
⚠️ 重要なポイント
並列では、合成抵抗は最も小さい抵抗よりもさらに小さくなります。道が増えるほど電流が流れやすくなるからです。
計算例:並列回路の合成抵抗
実際に計算してみましょう。3つの抵抗R₁=10Ω、R₂=20Ω、R₃=30Ωが並列に接続されている場合です。
💡 計算手順
1/R = 1/R₁ + 1/R₂ + 1/R₃
1/R = 1/10 + 1/20 + 1/30
1/R = 0.1 + 0.05 + 0.0333...
1/R = 0.1833...
R = 1 ÷ 0.1833 = 約5.46Ω
元の抵抗(10Ω、20Ω、30Ω)のどれよりも小さい5.46Ωになりました。これが並列回路の特徴です。
並列2個の場合の簡単な公式
抵抗が2個だけの並列回路では、もっと簡単な公式があります。
📐 並列2個の簡単公式
R = (R₁ × R₂) / (R₁ + R₂)
和分の積で一発計算!
直列 vs 並列|一目でわかる比較表
2つの回路の違いを整理しよう
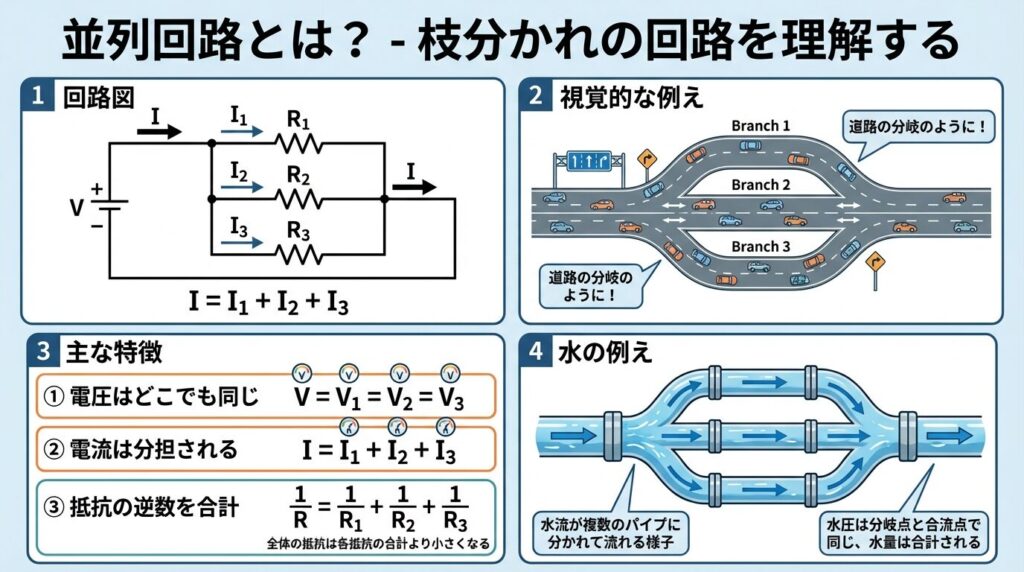
直列回路と並列回路の違いを、一覧表でまとめてみましょう。試験前の最終確認にも使えます。
| 項目 | 直列回路 | 並列回路 |
|---|---|---|
| 接続方法 | 数珠つなぎ(一直線) | 枝分かれ(並列) |
| 電流 | I = I₁ = I₂ = I₃ (どこでも同じ) |
I = I₁ + I₂ + I₃ (分岐して分担) |
| 電圧 | V = V₁ + V₂ + V₃ (分担される) |
V = V₁ = V₂ = V₃ (どこでも同じ) |
| 合成抵抗 | R = R₁ + R₂ + R₃ (足し算) |
1/R = 1/R₁ + 1/R₂ + 1/R₃ (逆数の足し算) |
| 特徴 | 抵抗が増えると 大きくなる |
抵抗が増えると 小さくなる |
回路判別のフローチャート
問題を解くときは、次の手順で回路のつながり方を確認しましょう。
📋 判別手順
- ステップ①:回路図をよく見る
- ステップ②:抵抗のつながり方を確認する
- ステップ③:一直線につながっている → 直列 → R = R₁ + R₂ + R₃
- ステップ④:枝分かれしている → 並列 → 1/R = 1/R₁ + 1/R₂ + 1/R₃
よくある間違い
並列回路の計算で、逆数を忘れるのが最も多い間違いです。
❌ 間違った計算
R = R₁ + R₂ + R₃ (これは直列の公式!)
✅ 正しい計算
1/R = 1/R₁ + 1/R₂ + 1/R₃ (逆数を忘れずに!)
並列では必ず「逆数を足してから、もう一度逆数にする」ことを忘れないようにしましょう。
実際の生活で見る直列回路と並列回路
直列回路の実例:イルミネーション
クリスマスのイルミネーションは、昔は直列回路でつながっていました。一つの電球が切れると、道が途切れてしまうため、全部の電球が消えてしまいます。
これは直列回路の一本道という特徴がよく表れている例です。
並列回路の実例:家庭のコンセント
家庭のコンセントは並列回路でつながっています。テレビを消しても、冷蔵庫は動き続けますよね。これは、それぞれが独立した道で電気を受け取っているからです。
並列回路なら、一つの機器が故障しても他の機器には影響しません。これが家庭の配線に並列回路が使われる理由です。
練習問題:混合回路を解いてみよう
実際の試験では、直列と並列が混ざった混合回路が出題されます。次のような手順で解きましょう。
🔍 混合回路の解き方
例題:10Ωと20Ωの抵抗が直列につながり、その合成抵抗が30Ωの抵抗と並列につながっている場合の合成抵抗は?
解答手順
- ステップ①:直列部分を先に計算 → R₁₂ = 10Ω + 20Ω = 30Ω
- ステップ②:並列部分を計算 → R₁₂と30Ωが並列
- ステップ③:1/R = 1/30 + 1/30 = 2/30 = 1/15
- ステップ④:R = 15Ω
答え:15Ω
混合回路は、内側(部分的なつながり)から順番に計算していくのがコツです。
まとめ:直列と並列の公式を確実にマスターしよう
この記事では、直列回路と並列回路の違いと、それぞれの合成抵抗の公式について解説しました。
📌 この記事のポイント
- 直列回路:数珠つなぎ、電流は同じ、電圧は分担、R = R₁ + R₂ + R₃
- 並列回路:枝分かれ、電圧は同じ、電流は分担、1/R = 1/R₁ + 1/R₂ + 1/R₃
- 並列2個の簡単公式:R = (R₁ × R₂) / (R₁ + R₂)
- 混合回路:内側(部分回路)から順番に計算する
直列回路は足し算、並列回路は逆数という違いをしっかり覚えておけば、電験三種の理論科目で確実に得点できます。
何度も練習問題を解いて、体で覚えてしまいましょう。理解が深まったら、次はオームの法則や抵抗率と導電率の記事も読んでみてください。