📊 こんな疑問、ありませんか?
- 分散分析表って、どうやって作るの?
- S、V、Fって何が違うの?
- 最終的に「F値」を出すまでの流れを知りたい!
こんにちは、シラスです。
前回、データのバラつき全体(ST)を、ナイフで2つに切り分けました。
🎯 群間平方和(SA)
温度を変えた効果(シグナル)
24
🎲 群内平方和(Se)
偶然の誤差(ノイズ)
4
「24対4」なら、明らかに効果の方が大きそうですよね。
しかし、統計学では「平方和(S)」をそのまま比べてはいけません。
⚠️ なぜダメなの?
データ数などの条件(自由度)が違うからです。
「総額」のまま比べると、不公平な勝負になってしまいます。
これらを公平な「単価(分散)」に直し、最終的な決着をつける場所。
それが今回完成させる「分散分析表(ANOVA Table)」です。
✅ この記事で学べること
- 分散分析表の全体像(ゴールを先に見る)
- ステップ1:SとfFを埋める
- ステップ2:分散(V)を計算する
- ステップ3:分散比(F値)を出す
- F値の意味:「シグナルはノイズの何倍?」
目次
1. 目指すゴール:この表を埋める
まずは、完成形の表を見ておきましょう。
実験計画法のゴールは、この表の右端にある「F値」を出すことです。
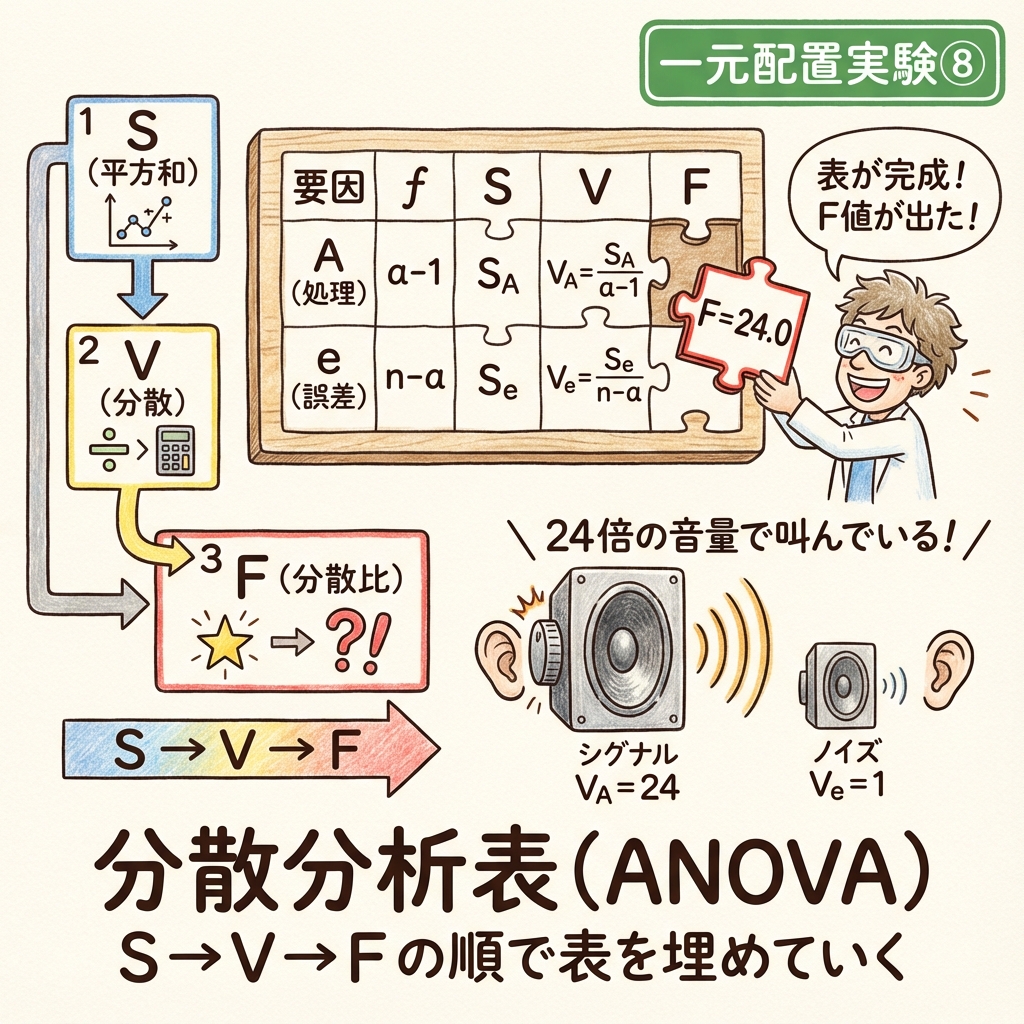
📋 分散分析表(空欄版)
空欄だらけに見えますが、恐れることはありません。
私たちはすでに「② ⑥ ⑨」の数字を持っています。
🤔 表の各列は何を表している?
f(自由度)
情報の「個数」
=データの広がり
S(平方和)
バラつきの「総額」
=エネルギーの塊
V(分散)
バラつきの「単価」
=S÷f
F(分散比)
シグナル÷ノイズ
=最終判定値
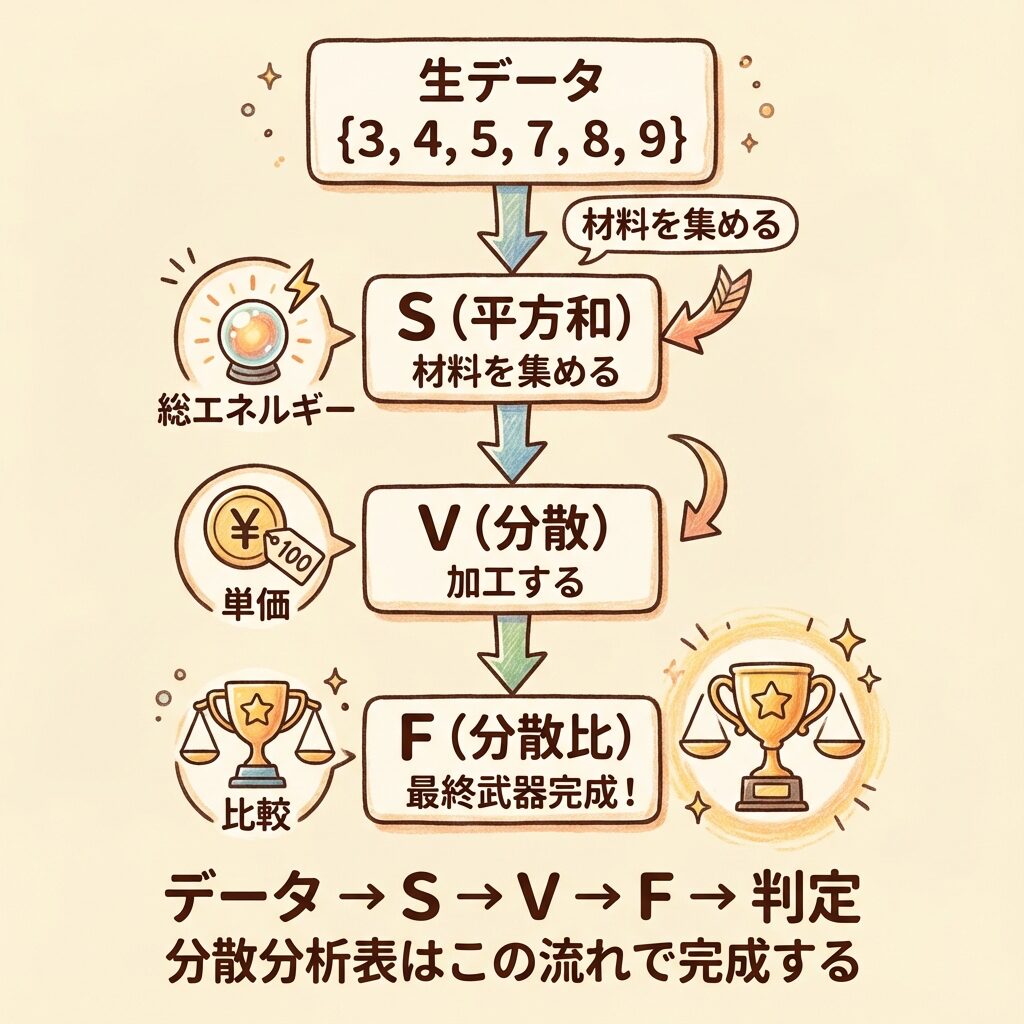
🎮 RPGで例えると
分散分析表を埋める作業は、RPGの装備強化に似ています。
⚔️
S(素材)
鉄鉱石を集める
🔨
V(加工)
単価に変換
🗡️
F(最終武器)
判定用の武器完成!
素材(S)を加工(÷f)して、最終武器(F値)を作る!

2. ステップ1:Sとfを埋める
前回の計算結果と、実験の条件(水準数・データ数)を整理して書き込みます。
📊 実験条件のおさらい
- 水準数 a = 2(低温・高温の2つ)
- データ総数 N = 6(各3個 × 2水準)
📝 平方和(S)を埋める
これは前回計算済みですね。そのまま書き込みます。
SA(温度)
24
Se(誤差)
4
ST(計)
28
📝 自由度(f)を埋める
自由度は「情報の広さ(数 − 1)」でした。
fA(温度) = 水準数 − 1 = 2 − 1 = 1
fT(計) = データ総数 − 1 = 6 − 1 = 5
fe(誤差) = 引き算(fT − fA)= 5 − 1 = 4
💡 なぜ「−1」するの?
「合計が決まっていると、最後の1つは自動的に決まる」からです。
例:3人で100円を分けるとき、2人の取り分が決まれば、3人目は自動的に決まりますよね。
→ 自由に決められるのは「数 − 1」個だけ
✅ ステップ1完了!表の左半分が埋まった
| 要因 | f ✅ | S ✅ | V | F |
|---|---|---|---|---|
| A:温度 | 1 | 24 | ? | ? |
| e:誤差 | 4 | 4 | ? | − |
| 計 | 5 | 28 | − | − |
✅ fとSの列が埋まりました!次はV(分散)を計算します

3. ステップ2:分散(V)を計算する
ここからが割り算です。
平方和(総エネルギー)を自由度(個数)で割って、「1単位あたりのエネルギー(単価)」を出します。
📐 分散(V)の公式
V = S ÷ f
分散 = 平方和 ÷ 自由度(=総額 ÷ 個数 = 単価)
🥩 お肉のたとえ(復習)
前に「お肉のパック」で説明しましたね。
🥩
S(平方和)= 総額
「このパック、1000円です」
⚖️
f(自由度)= グラム数
「10kgです」
💰
V(分散)= 単価
「100円/kgですね」
総額を個数で割れば、単価が出る。これだけです!
🏭 実践計算
🌡️ 温度の分散 VA
SA ÷ fA = 24 ÷ 1
= 24
シグナルの「単価」
🎲 誤差の分散 Ve
Se ÷ fe = 4 ÷ 4
= 1
ノイズの「単価」(基準値)
💡 Ve = 1 の意味
この「Ve = 1」という数字が、この実験における「ノイズの大きさ(基準)」になります。
次のステップで、シグナル(VA)がこの基準の何倍かを計算します。
✅ ステップ2完了!V列が埋まった
| 要因 | f ✅ | S ✅ | V ✅ | F |
|---|---|---|---|---|
| A:温度 | 1 | 24 | 24 | ? |
| e:誤差 | 4 | 4 | 1 | − |
| 計 | 5 | 28 | − | − |
✅ V(分散)の列が埋まりました!あとはF値だけ!

4. ステップ3:分散比(F値)を出す
いよいよクライマックスです。
「温度の効果(VA)」は、「ノイズ(Ve)」の何倍大きいのか?を計算します。
📐 F値(分散比)の公式
F = VA ÷ Ve
シグナルの単価 ÷ ノイズの単価 = 「何倍?」
📻 ラジオのたとえ(復習)
F値は、「シグナル対ノイズ比(S/N比)」のようなものです。
🔊
シグナル(VA)
聞きたい音楽の音量
24
📢
ノイズ(Ve)
ザーザーという雑音
1
シグナルがノイズの何倍の音量で鳴っているか?
その倍率がF値です。
🏭 実践計算
最終計算
F = VA ÷ Ve
= 24 ÷ 1
= 24.0
🎉 F値は 24.0 になりました!
これは、「温度を変える効果は、偶然のノイズよりも24倍も強力だ!」ということを意味しています。
🔊 音量でイメージすると
F = 24 ということは…
ノイズ(雑音)
1
シグナル(音楽)
24
雑音の24倍の声量で叫んでいるようなもの。
間違いなく聞こえますよね!

まとめ:完成した分散分析表
計算結果を清書すると、こうなります。
🎉 分散分析表(ANOVA Table)完成!
📝 今日のポイント
Step1:SとfFを埋める(前回の計算結果 + 水準数・データ数から)
Step2:V = S ÷ f(総額を個数で割って単価に)
Step3:F = VA ÷ Ve(シグナルはノイズの何倍?)
表が埋まりました。しかし、まだ終わりではありません。
⚠️ F値が「24.0」だからといって、勝手に「合格!」と決めてはいけません。
「統計的に見て、24.0 は本当にレアなのか?」を判定する、最後の審判が待っています。
📖 次に読む記事
F検定で有意差を判定する|F分布表の使い方|一元配置実験⑨
今回出した「F = 24.0」が統計的に意味のある数字なのか?F分布表を使って「合格・不合格」を判定する方法を解説します!
次の記事を読む →📚 あわせて読みたい
📖 一元配置実験マスター講座【全16回】
このシリーズを順番に読めば、一元配置実験を完全マスターできます!