こんにちは、シラスです。
実験計画を立てていると、こんな「現場あるある」にぶつかることがよくあります。
「でも、手元のL8直交表は『2水準』専用だ…」
因子がすべて2択ならいいのですが、現実はそう甘くありません。
「材料A, B, C」のような3択の因子が1つ混ざっただけで、L8は使えなくなってしまうのでしょうか?
それとも、わざわざ実験回数の多いL27(3水準系)を使わなきゃいけないのでしょうか?
いいえ、諦める必要はありません。
2水準の表に3水準をねじ込む裏技、「ダミー水準法(擬水準法)」を使えば解決できます。
今日は、この現場で必須のテクニックについて、仕組みと計算方法を解説します。
目次
1. ダミー水準法のアイデア
L8直交表の各列には、「1」か「2」しか入りません。
ここに「3(材料C)」を入れたいのです。
どうすればいいでしょうか?
答えはシンプルです。
1つをダミー(空席)にする」
2列使えば $2 \times 2 = 4$ 通り
L8直交表の任意の2列(例えば第1列と第2列)を組み合わせると、以下の4パターンが作れます。
- (1, 1) → これを「材料A」とする
- (1, 2) → これを「材料B」とする
- (2, 1) → これを「材料C」とする
- (2, 2) → 余った!
この余った「(2, 2)」の枠に、すでに登場した材料(例えばA)をもう一度割り当てる(ダミーとして入れる)のです。
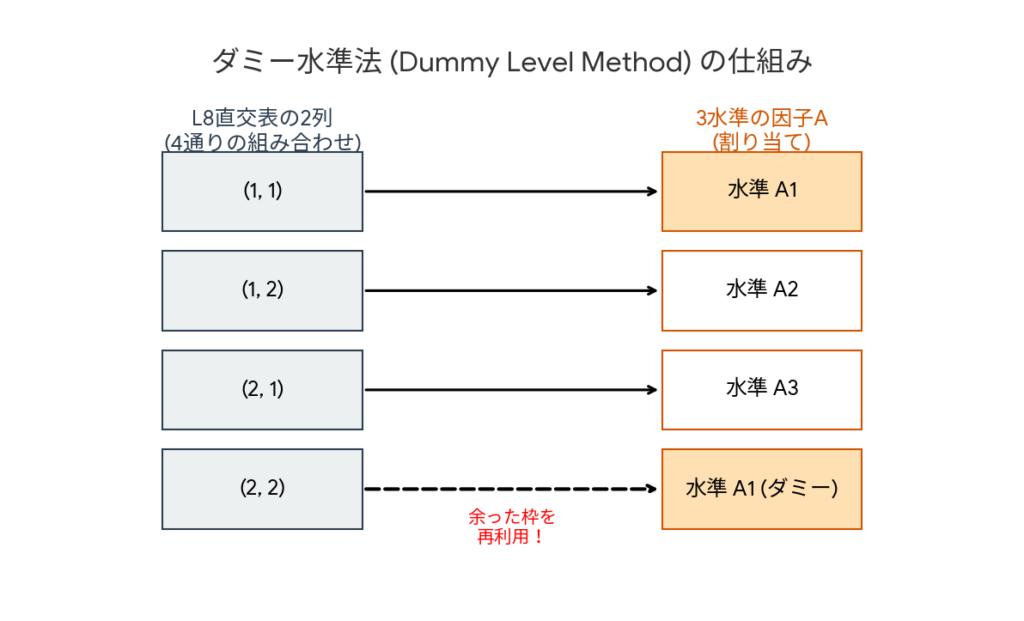
こうすれば、見かけ上は4水準ですが、実質は3種類の材料で実験を行うことができます。
これがダミー水準法です。
2. 割り付けのルール(線点図を使う)
ただし、どの2列でも良いわけではありません。
4通りの組み合わせを作るためには、「交互作用が出る列」もセットで消費する必要があります。
- 第1列と第2列を使うと、その相互作用は第3列に出ます。
- つまり、ダミー水準法を行うには、「1, 2, 3」の3列セットを占有します。
【コスト】
3水準の因子を1つ入れるために、L8の貴重な列を3つも消費してしまいます。
(残り4列しか使えなくなります。ここが注意点です)
3. 解析の注意点:補正が必要
実験が終わった後、解析(分散分析)をする際に一つだけ問題が起きます。
「材料Aだけ、データ数が2倍ある(エコヒイキされている)」ことです。
- 材料A: 4回登場(本物2回+ダミー2回)
- 材料B: 2回登場
- 材料C: 2回登場
データ数が不揃い(アンバランス)なので、普通に計算すると平方和($S$)がおかしくなります。
そこで、専用の補正式を使います。
ダミー水準法の平方和($S_{A'}$)
※材料Aの合計($T_A$と$T_{A'}$)を足して、分母(データ数)も2倍にする。
要するに、「多いやつは多いなりに、少ないやつは少ないなりに、重み付けをして公平にする」計算を行うわけです。
まとめ
このテクニックを知っていれば、「材料が3つあるからL8は使えない…諦めて総当たりしよう…」という悲劇を回避できます。
L8直交表は、工夫次第でどんな形にも変形できる万能ツールなのです。
次回は、さらに応用して「4水準」を作る方法についても解説します。
📚 実験計画法の「挫折」を救う2冊
「数式を見た瞬間に本を閉じた」
そんな経験がある私だからこそ推せる、厳選のバイブルです。