📌 この記事はこんな人におすすめ
- 直交表の「使い方」は知っているけど、「なぜ減らせるか」がモヤモヤする
- QC検定や技術士試験で直交表が出てきて、本質を理解したい
- 教科書の説明が数式ばかりで、イメージがつかめない
- 実務で直交表を使っているけど、なぜ成立するのか説明できない
「直交表を使えば、実験回数を大幅に減らせます」
実験計画法の教科書には、必ずこう書いてあります。
そして、L4、L8、L12といった直交表の「使い方」は丁寧に解説されています。
でも、こんな疑問を持ったことはありませんか?
🤔 みんなが抱える「モヤモヤ」
- なぜ128回の実験が8回で済むの?
- 間引いて大丈夫なの?情報が欠落しない?
- 「直交」って何?なぜ直交だと減らせる?
- そもそも、この「魔法」の正体は何?
私も最初は同じでした。
「使い方」は覚えたけど、「なぜ」がわからない。
試験には受かったけど、人に説明できない。
でも、あるとき気づいたんです。
直交表は「魔法」ではなく「数学」だったと。
そして、その仕組みを理解したとき、
「なるほど、だから減らせるのか!」とスッキリしました。
💡 この記事のゴール
直交表が実験回数を減らせる「3つの原理」を、中学生でもわかるように解説します。
この記事を読み終えたとき、あなたは「なぜ直交表で実験を減らせるのか」を誰にでも説明できるようになっています。
目次
まず「全組み合わせ実験」の問題点を理解しよう
直交表の価値を理解するには、まず「直交表を使わない場合」の問題点を知る必要があります。
【例題】最高のカレーを作りたい!
あなたは「最高においしいカレー」を作るための実験をしたいと考えています。
調整できる要素(因子)は以下の7つ。それぞれ2つの選択肢(水準)があります。
| 因子 | 水準1 | 水準2 |
|---|---|---|
| A:肉の種類 | 豚肉 | 鶏肉 |
| B:玉ねぎの量 | 少なめ | 多め |
| C:煮込み時間 | 30分 | 60分 |
| D:スパイスの量 | 控えめ | 多め |
| E:隠し味 | チョコ | コーヒー |
| F:ルーの種類 | 甘口 | 辛口 |
| G:仕上げ | バター | なし |
全組み合わせ(総当たり)だと何回必要?
すべての組み合わせを試す「総当たり実験」をするとします。
2 × 2 × 2 × 2 × 2 × 2 × 2 = 27 = 128回
128種類のカレーを作って、それぞれ味見して評価する。
現実的に不可能ですよね。
時間もコストも膨大。さらに、128回も味見したら味覚がおかしくなります。
直交表(L8)を使うと、たった8回で済む
ここで登場するのが直交表です。
L8直交表を使えば、7因子2水準の実験がたった8回で完了します。
128回 → 8回
実験回数が 1/16 に激減!
でも、ここで当然の疑問が生まれます。
❓ 素朴な疑問
「128通りあるのに、8回しか試さなくて大丈夫なの?」
「残り120通りの情報は、どこに消えたの?」
「間引いたせいで、間違った結論を出さない?」
この疑問に答えるのが、この記事の目的です。

直交表が実験を減らせる「3つの原理」
直交表が128回を8回に減らせるのは、「魔法」でも「手抜き」でもありません。
数学的に正しい3つの原理に基づいています。
🔑 直交表の3つの原理
原理①:バランス(均等出現)
各因子の各水準が、同じ回数だけ登場する
原理②:直交性(独立性)
任意の2因子の組み合わせが、すべて同じ回数だけ登場する
原理③:効果の分離
各因子の効果を、他の因子の影響を受けずに計算できる
この3つが揃っているから、「間引いても正しい結果が出る」のです。
1つずつ、具体例で見ていきましょう。
原理①:バランス(均等出現)
「バランス」とは何か?
バランスとは、各因子の各水準が、実験全体で同じ回数だけ登場することです。
L8直交表を見てみましょう。
| 実験No. | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 2 | 2 | 2 | 2 |
| 3 | 1 | 2 | 2 | 1 | 1 | 2 | 2 |
| 4 | 1 | 2 | 2 | 2 | 2 | 1 | 1 |
| 5 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| 6 | 2 | 1 | 2 | 2 | 1 | 2 | 1 |
| 7 | 2 | 2 | 1 | 1 | 2 | 2 | 1 |
| 8 | 2 | 2 | 1 | 2 | 1 | 1 | 2 |
因子Aの列を見てください。
- 水準1(赤)が登場する回数:4回(実験No.1,2,3,4)
- 水準2(青)が登場する回数:4回(実験No.5,6,7,8)
ぴったり半分ずつ。これがバランスです。
他の因子B〜Gも、すべて水準1が4回、水準2が4回です。
なぜバランスが重要なのか?
バランスが取れていないと、公平な比較ができないからです。
❌ バランスが崩れた例
もし因子A(肉の種類)で、豚肉が7回、鶏肉が1回しか登場しなかったら?
「豚肉の平均点」と「鶏肉の平均点」を比較しても、データ数が違いすぎて公平じゃない。
鶏肉の1回がたまたま良かった(悪かった)だけかもしれない。
✅ バランスが取れている場合
豚肉4回、鶏肉4回なら、同じ条件で比較できる。
どちらも4回分のデータがあるので、平均を比較しても公平。

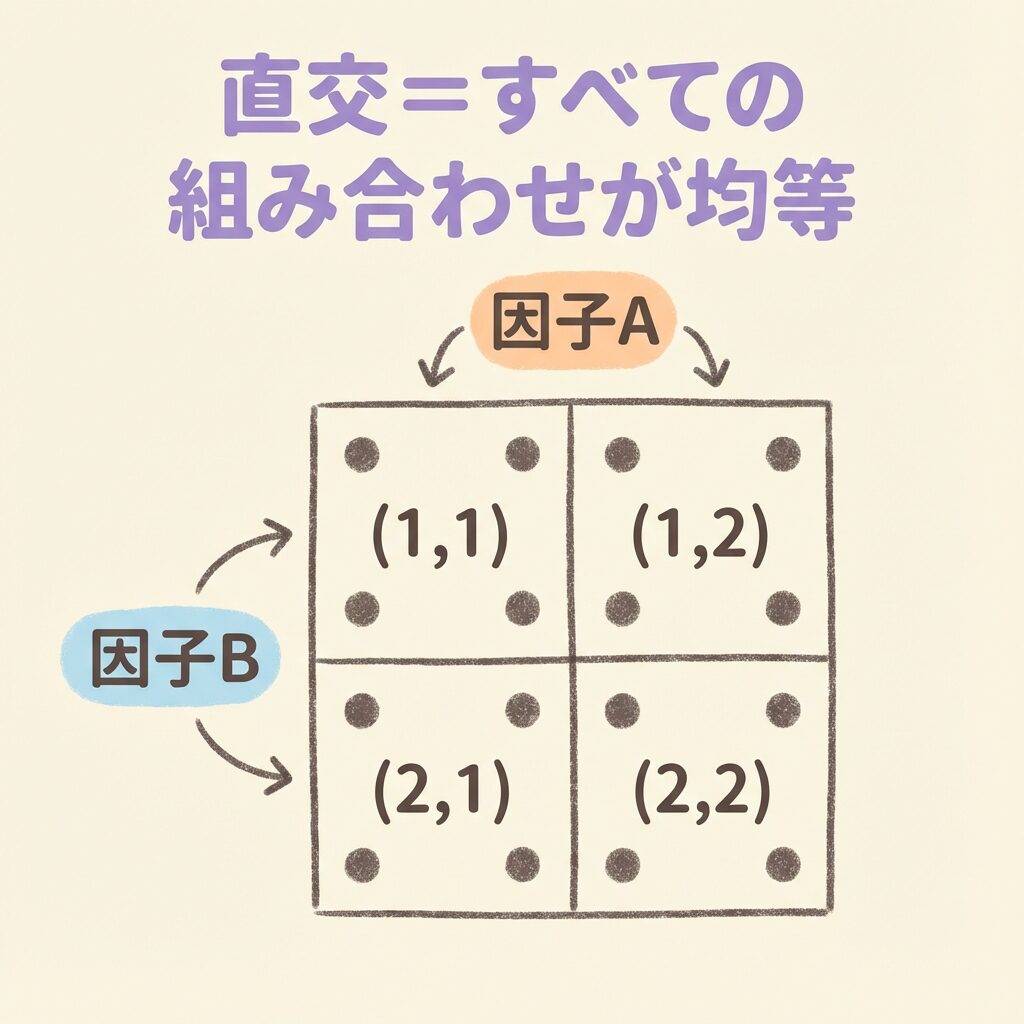
原理②:直交性(独立性)
ここが最も重要で、「直交表」という名前の由来でもあります。
「直交」とは何か?
直交とは、数学的には「ベクトルの内積がゼロ」という意味ですが、
実験計画法では「任意の2列の組み合わせが、すべて同じ回数だけ登場する」という性質を指します。
言葉だけではわかりにくいので、具体的に見てみましょう。
【具体例】因子Aと因子Bの組み合わせを数える
L8直交表で、因子Aと因子Bの組み合わせを数えてみましょう。
| 実験No. | 因子A | 因子B | 組み合わせ |
|---|---|---|---|
| 1 | 1 | 1 | (1,1) |
| 2 | 1 | 1 | (1,1) |
| 3 | 1 | 2 | (1,2) |
| 4 | 1 | 2 | (1,2) |
| 5 | 2 | 1 | (2,1) |
| 6 | 2 | 1 | (2,1) |
| 7 | 2 | 2 | (2,2) |
| 8 | 2 | 2 | (2,2) |
組み合わせの出現回数を数えると、
| (1,1):2回 | (1,2):2回 |
| (2,1):2回 | (2,2):2回 |
すべて2回ずつ!これが「直交」!
この性質は、どの2列を選んでも成り立ちます。
AとB、AとC、BとD、EとG…すべての2列の組み合わせが「均等」なのです。
なぜ直交性が重要なのか?
直交性があると、因子の効果が「混ざらない」のです。
🍛 カレーの例で考える
「豚肉のときは玉ねぎ多め」「鶏肉のときは玉ねぎ少なめ」
という組み合わせが偏っていたらどうなるでしょう?
「豚肉がおいしい」のか「玉ねぎ多めがおいしい」のか、
区別がつかなくなります。
これが交絡(こうらく)という問題です。
直交表は、すべての組み合わせが均等なので、交絡が起きない。
だから、各因子の効果を独立して評価できるのです。
【たとえ話】アンケート調査で考える
直交性をもっと身近な例で考えてみましょう。
📊 ダメなアンケート調査
「コーヒーが好きか?」と「朝型か夜型か?」を調査したい。
ダメな調査:
朝の7時にオフィスで調査 → 朝型の人ばかり
朝型の人はコーヒー好きが多いかも?
→ 「コーヒー好き」と「朝型」が混ざってしまう
良い調査:
朝型×コーヒー好き、朝型×コーヒー嫌い、
夜型×コーヒー好き、夜型×コーヒー嫌い
を同じ人数ずつ集める → 直交している!
原理③:効果の分離(なぜ128回が8回で済むのか)
ここまでで「バランス」と「直交性」を理解しました。
でも、まだ核心の疑問が残っています。
❓ 核心の疑問
128通りの組み合わせのうち、8通りしか試していない。
残り120通りの情報は、本当に不要なの?
答えは、「不要な情報」ではなく「知りたい情報を効率よく得ている」です。
【核心】私たちが本当に知りたい情報は何か?
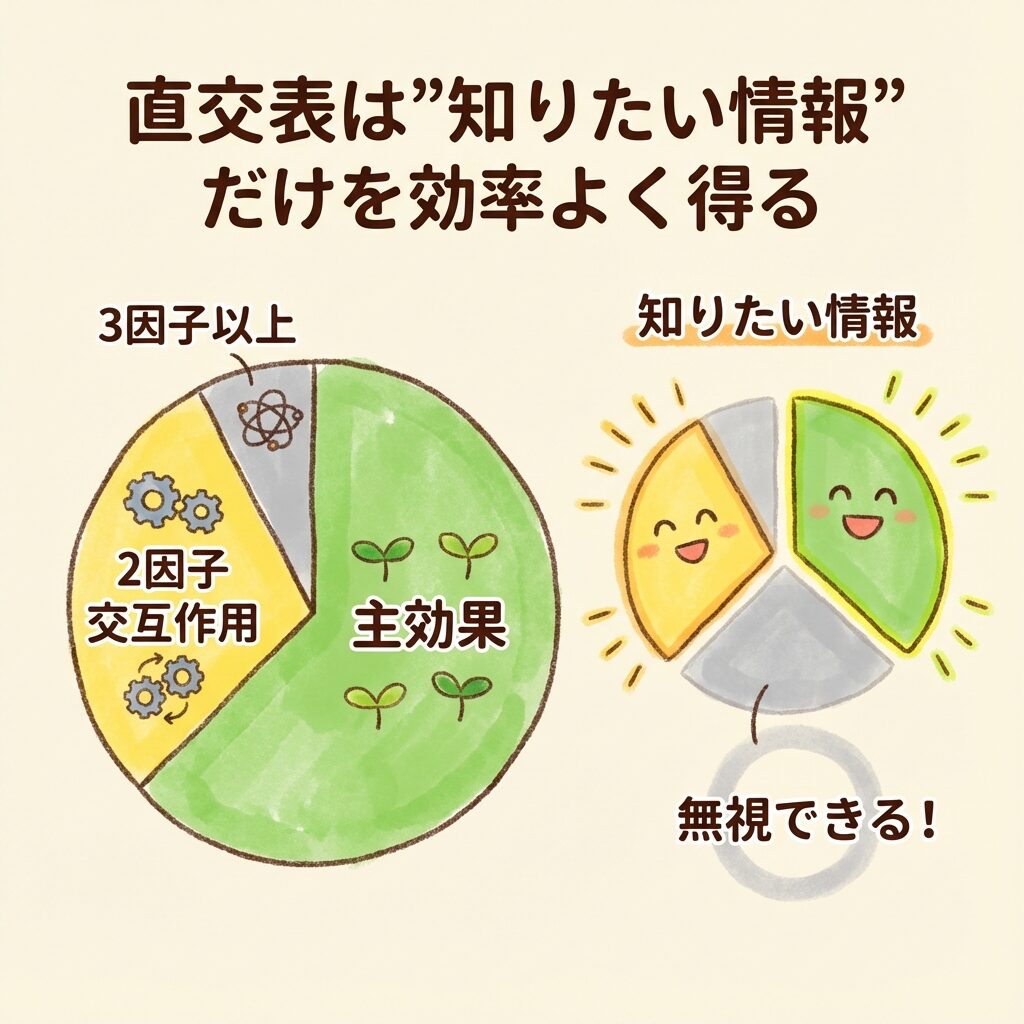
128回の総当たり実験で得られる情報を整理してみましょう。
📊 128回の実験で得られる情報
| 主効果(7つ) | A, B, C, D, E, F, G それぞれの効果 |
| 2因子交互作用(21個) | A×B, A×C, A×D, ... など |
| 3因子交互作用(35個) | A×B×C, A×B×D, ... など |
| 4因子以上の交互作用 | A×B×C×D, ... など(さらに多数) |
しかし、現実の実験では3因子以上の交互作用はほぼ無視できることが知られています。
カレーの例で言えば、
「肉×玉ねぎ×煮込み時間×スパイス×隠し味」の5因子が同時に影響し合う…
なんてことは、現実にはほぼ起きないのです。
💡 重要な原則
実験で本当に知りたいのは、ほとんどの場合、
①主効果と②2因子交互作用だけ。
3因子以上の交互作用は「無視しても問題ない」という
「効果のスパース性」の原則があります。
直交表は「知りたい情報」だけを効率よく得る
L8直交表で8回の実験をすると、以下の情報が得られます。
| 情報の種類 | 128回総当たり | L8(8回) |
|---|---|---|
| 主効果(7因子) | ✅ 得られる | ✅ 得られる |
| 2因子交互作用 | ✅ 得られる | ⚠️ 交絡する |
| 3因子以上の交互作用 | ✅ 得られる | - 無視 |
ポイントは、「主効果」は完璧に分離できるということ。
バランスと直交性があるおかげで、
「どの因子がどれだけ効果があるか」は、8回の実験で正確にわかるのです。
【たとえ話】クラスの平均点を知りたいとき
もう1つ、身近な例で考えてみましょう。
🏫 クラスの平均点を調べたい
30人のクラスがあります。全員のテストの点数を知りたい。
方法A(総当たり):
30人全員に聞く → 完璧なデータが得られる
方法B(サンプリング):
男女比・成績順が均等になるように8人だけ選んで聞く
→ 「平均点」は、ほぼ正確に推定できる
方法Bでは「各個人の点数」はわからないけど、
「クラスの傾向」を知るには十分。
これが直交表の考え方と同じです。
【図解まとめ】直交表が実験を減らせる仕組み
ここまでの内容を、1枚の図にまとめます。
🎯 直交表で実験回数を減らせる3つの理由
理由①:バランスがある
各因子の各水準が同じ回数登場する
→ 公平に比較できる
理由②:直交性がある
任意の2因子の組み合わせが均等に登場する
→ 因子の効果が混ざらない(交絡しない)
理由③:必要な情報に絞っている
主効果は完璧に分離できる
3因子以上の交互作用は現実的に無視できる
→ 「知りたい情報」を効率よく得られる
直交表の「代償」も知っておこう
直交表は万能ではありません。
実験回数を減らす代わりに、失うものもあります。
代償①:交互作用が交絡する
L8直交表で7因子を割り付けると、2因子交互作用が他の効果と混ざってしまいます。
例えば、「A×B」の交互作用と「C」の主効果が区別できなくなる、など。
これを交絡(エイリアス)と呼びます。
交互作用が重要な実験では、L8ではなくL16など、より大きな直交表を使う必要があります。
代償②:最適な組み合わせがわからないことがある
128通りのうち8通りしか試していないので、
「試していない組み合わせが実は最高だった」という可能性はあります。
ただし、主効果が正しく評価できていれば、
「各因子のベストな水準」を組み合わせることで、最適解に近い条件は見つけられます。
次に学ぶべきこと
直交表の「なぜ」がわかったら、次は「どう使うか」を学びましょう。
📚 直交表を使いこなすための記事
【完全版】実験計画法の学習マップ|基礎から直交表・応用までを体系的に学ぶ →
まとめ:直交表は「魔法」ではなく「数学」
📌 この記事のポイント
- 直交表は「バランス」「直交性」「効果の分離」の3原理で成り立っている
- バランス:各水準が同じ回数登場 → 公平な比較ができる
- 直交性:2因子の組み合わせが均等 → 効果が混ざらない
- 効果の分離:主効果は完璧に分離できる → 知りたい情報が得られる
- 3因子以上の交互作用は現実的に無視できるため、128回→8回でも問題ない
直交表は、「間引き」ではなく「効率的な選択」です。
128通りすべてを試さなくても、
「知りたい情報(各因子の効果)」は8回で正確に得られる。
それを数学的に保証しているのが、「直交性」という性質なのです。
「使い方」を覚えるだけでなく、「なぜ」を理解する。
それができれば、試験でも実務でも、自信を持って直交表を使いこなせるようになります。
最後まで読んでいただき、ありがとうございました。
「直交表って結局何なの?」というモヤモヤが、
「なるほど、だから減らせるのか!」に変わっていれば嬉しいです。
次は、ぜひL4・L8直交表の具体的な使い方を学んでみてください。

