📌 この記事の目的
一元配置実験の計算は、「修正項 → 平方和 → 分散 → F値」という流れで進みます。
今回は「なぜその計算をするのか」は説明しません。
まずは「どこに向かっているのか」という全体像(地図)を頭に入れることがゴールです。
😔 こんな経験ありませんか?
- 「修正項」「平方和」「自由度」…いきなり計算が始まって混乱した
- 参考書を読んでも「なぜこの計算をするのか」が全然わからない
- 計算を進めているけど、どこに向かっているのかわからない
- 分散分析表を見ても、何がゴールなのかピンとこない
安心してください。これは誰もが通る道です。
実験計画法の参考書は、いきなり「修正項を計算します」から始まることが多いです。でも、ゴールが見えないまま計算を始めても、迷子になるだけですよね。
そこで今回は、計算の「理由」は後回しにして、「全体の流れ」だけを先にお見せします。
🗺️ たとえるなら「旅行の地図」
旅行に行くとき、まず「どこに行くか(ゴール)」を決めますよね。
ゴールがわかれば、「どの道を通るか(ルート)」が見えてきます。
一元配置実験も同じです。
「分散分析表を完成させる」というゴールがわかれば、
「修正項 → 平方和 → 分散 → F値」という道順が腑に落ちます。
この記事を読み終わる頃には、「ああ、だからこの順番で計算するのか!」とスッキリしているはずです。
目次
🏁 まずはゴールを確認しよう
結論から言います。
一元配置実験のゴールは、「分散分析表(ANOVA表)」を完成させることです。
まずは完成形を見てみましょう。これがゴールです。
完成形:分散分析表(ANOVA表)
| 要因 | 平方和(S) | 自由度(f) | 分散(V) | F値 | 判定 |
|---|---|---|---|---|---|
| 因子A | 24.0 | 2 | 12.0 | 24.0 | ** |
| 誤差(e) | 3.0 | 6 | 0.5 | - | - |
| 計(T) | 27.0 | 8 | - | - | - |
「うわ、数字がいっぱい…」と思いましたか?大丈夫です。
今は「この表を埋めることがゴールなんだな」ということだけ覚えてください。
🎯 この表が完成すると何がわかる?
「因子Aは結果に影響しているか?」が、
数値(F値)と判定(** や * )でハッキリわかります。
つまり、「肉の種類でカレーの味は変わるか?」という疑問に、「はい、確実に変わります(有意差あり)」と科学的に答えられるようになるのです。
🗺️ 分散分析表を作る「5つのステップ」
ゴールがわかったところで、次は「どうやってそこにたどり着くか」を見ていきましょう。
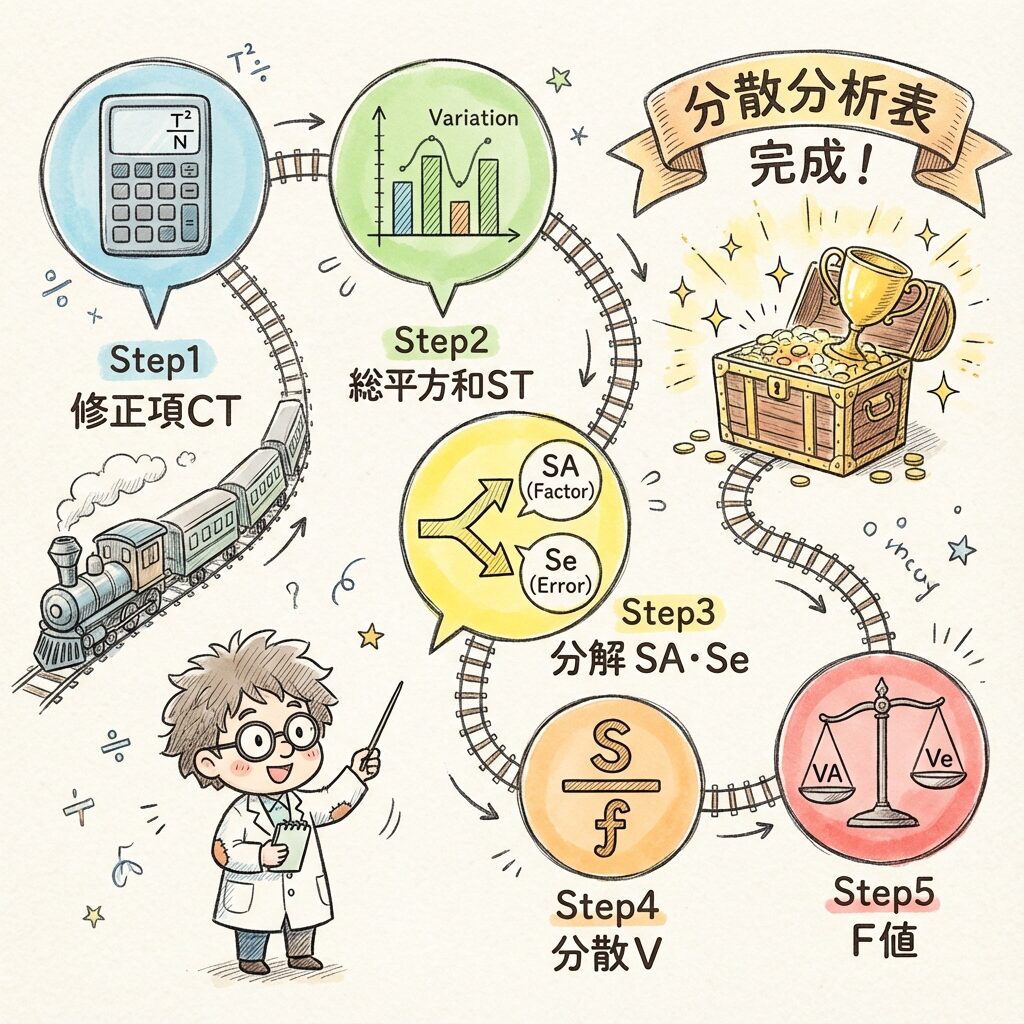
分散分析表を完成させるには、5つのステップを順番に進みます。
🚀 計算の5ステップ(全体像)
Step 1:修正項(CT)を計算する
↓
Step 2:総平方和(ST)を計算する
↓
Step 3:平方和を「因子」と「誤差」に分解する(SA、Se)
↓
Step 4:分散(V)を計算する
↓
Step 5:F値を計算して判定する
↓
🏁 分散分析表の完成!
今は「ふーん、5つあるのか」くらいで大丈夫です。
次から、各ステップを「何をするのか」だけザッと説明します。「なぜその計算をするのか」は次回以降の記事で詳しく解説しますので、今回は流れをつかむことに集中してください。
一元配置実験とは?1つの因子で白黒つける実験の基本形 →
📋 各ステップでやることを確認しよう
各ステップで「何をするのか」を、料理のレシピのようにザッと見ていきます。理由は後回し。まずは流れだけです。
Step 1:修正項(CT)を計算する
CT = T² / N
(全データの合計)²÷(データの個数)
ひとことで言うと:データ全体の「基準点」を作る計算です。
詳しくは → 修正項(CT)とは?|一元配置実験④
Step 2:総平方和(ST)を計算する
ST = Σx² − CT
(各データの2乗の合計)−(修正項)
ひとことで言うと:データ全体の「バラつきの総量」を計算します。
詳しくは → 総平方和(S_T)の計算|一元配置実験⑥
Step 3:平方和を「因子」と「誤差」に分解する
ST = SA + Se
(総バラつき)=(因子による効果)+(誤差)
ひとことで言うと:バラつきを「因子の効果」と「偶然の誤差」に分けます。
詳しくは → 群間平方和と群内平方和|一元配置実験⑦
Step 4:分散(V)を計算する
V = S ÷ f
(平方和)÷(自由度)
ひとことで言うと:バラつきを「1個あたり」に換算します。
詳しくは → 分散分析表(ANOVA)の作り方|一元配置実験⑧
Step 5:F値を計算して判定する
F = VA ÷ Ve
(因子の分散)÷(誤差の分散)
ひとことで言うと:「因子の効果」が「誤差」の何倍大きいか計算します。
F値が大きければ「因子に効果あり!」と判定できます。
詳しくは → F検定で有意差を判定する|一元配置実験⑨
🎨 全体像をイメージで理解しよう
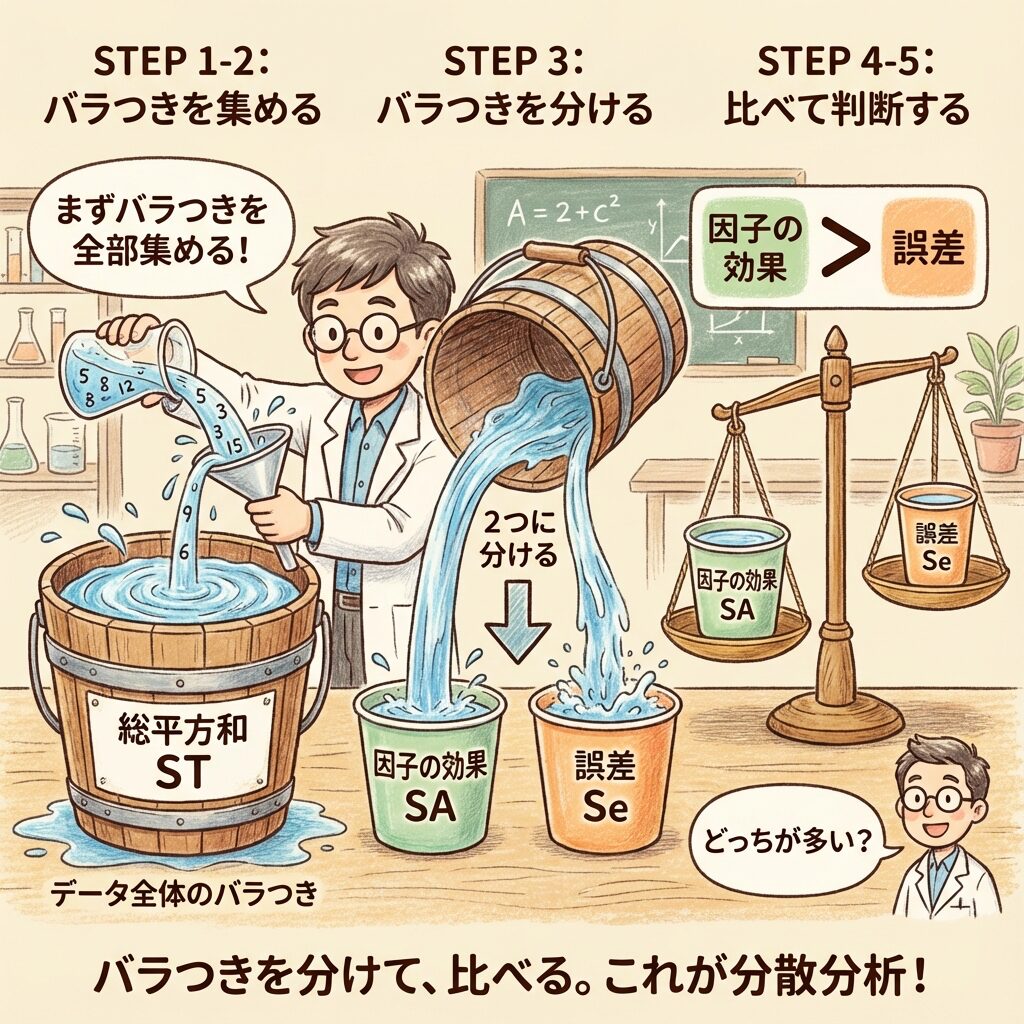
文字だけではわかりにくいので、計算の流れを「水の流れ」にたとえてみます。
💧 計算の流れを「水」でイメージ
🪣 Step 1〜2(修正項・総平方和)
まず、バケツに「水(データのバラつき)」を全部集めます。
これが総平方和(ST)です。
🔀 Step 3(分解)
集めた水を、2つのコップに分けます。
・「因子の効果」のコップ → SA
・「偶然の誤差」のコップ → Se
📏 Step 4(分散)
各コップの水を「1杯あたり」に計算し直します。
これが分散(V)です。
⚖️ Step 5(F値)
「因子のコップ」と「誤差のコップ」を比べます。
因子のコップの方が明らかに多ければ、「因子に効果あり!」と判定。
📊 分散分析表と5ステップの対応
最後に、5ステップで計算した数値が、分散分析表のどこに入るかを確認しましょう。
| ステップ | 計算するもの | 表のどこに入る? |
|---|---|---|
| Step 1 | 修正項(CT) | 表には入らない(計算の準備) |
| Step 2 | 総平方和(ST) | 「計」の行の平方和 |
| Step 3 | SA、Se | 因子A・誤差の行の平方和 |
| Step 4 | VA、Ve | 因子A・誤差の行の分散 |
| Step 5 | F値 | 因子Aの行のF値 |
この対応がわかれば、「何のためにこの計算をしているのか」が見えてきますね。
💡 気づきましたか?
分散分析表は「左から右へ」埋めていきます。
平方和 → 分散 → F値の順番です。
そして、平方和を求めるために「修正項」が必要なので、
計算は修正項が一番最初になるのです。
📝 まとめ
この記事のポイント
- ゴール:分散分析表を完成させて「因子に効果があるか」を判定する
- 5ステップ:修正項 → 総平方和 → 分解 → 分散 → F値
- 表は左から右へ:平方和 → 分散 → F値 の順に埋める
- 今回は「流れ」だけ。「なぜ」は次回以降で解説
🌸 今の段階で完璧に理解しなくて大丈夫です
「なんとなく流れはわかったかも…?」くらいで十分です。
次回からの記事で、各ステップを丁寧に解説していきます。
この「地図」を持っていれば、迷子になりません。
次回は、いよいよ計算の第一歩。「修正項(CT)」とは何か?を図解で解説します。「なぜT²/Nを計算するのか」がスッキリわかりますよ。
📖 次に読む記事
一元配置実験シリーズ|次の記事
修正項(CT)とは?T²/Nの計算式を図解で理解する|一元配置実験④
分散分析の計算で最初に登場する「修正項(CT)」。なぜT²/Nを計算するのか?データの「底上げ分」を取り除く理由を、図解でわかりやすく解説します。
次の記事を読む →🔗 関連記事
分散分析とは?「平均の差」ではなく「分散」を見る理由|一元配置実験① →
一元配置実験とは?1つの因子で白黒つける実験の基本形|一元配置実験② →
誤差とは?実験で避けられないバラつきの正体|実験計画法の基礎概念⑩ →
📚 一元配置実験シリーズ|全16回
このシリーズを順番に読めば、一元配置実験を完全マスターできます。
- 分散分析とは?「平均の差」ではなく「分散」を見る理由
- 一元配置実験とは?1つの因子で白黒つける実験の基本形
- 一元配置実験の計算の全体像|分散分析表を作るまでの地図 ← 今ここ
- 修正項(CT)とは?T²/Nの計算式を図解で理解する
- 平方和(S)と自由度の関係|「分散」を求める準備
- 総平方和(S_T)の計算|データ全体のバラつきを数値化する
- 群間平方和と群内平方和|バラつきを「効果」と「誤差」に分解する
- 分散分析表(ANOVA)の作り方|表を完成させる手順
- F検定で有意差を判定する|F分布表の使い方
- 母平均の点推定と区間推定|最適条件の結果を予測する
- 有効繰返し数とは?実験回数の最適解を導く考え方
- 有効繰返し数の計算方法|2つの公式を使い分ける
- 平均平方の期待値E(V)とは?数式の意味を直感的に理解する
- 分散分析表の作り方完全ガイド|S→V→Fの流れを総復習
- 一元配置実験の分散分析を実践|カレーの例で手を動かす
- 一元配置実験の計算を完全図解|分散分析表を1から作る全手順
🗺️ 全体像(地図)を手に入れました!
次回から、1ステップずつ攻略していきましょう。
