📌 この記事でわかること
- 2水準系直交表の分散分析の全体フロー
- 列平方和の2つの求め方(一般式と簡便式)
- 誤差列の見つけ方と誤差平方和の計算
- 主効果・交互作用の平方和と自由度
- 最適条件における母平均の点推定
- 点推定値の分散の推定と有効繰返し数
「直交表の分散分析、一元配置と何が違うの?」
「列平方和の公式が2つあって、どっちを使えばいいかわからない…」
「誤差列って何?どうやって見つけるの?」
QC検定1級を目指す方なら、こんな悩みを抱えているのではないでしょうか。
直交表の分散分析は、一元配置や二元配置と考え方は同じです。ただし、「列ごとに計算する」という独特のルールがあるため、最初は混乱しやすいポイントでもあります。
結論から言うと、直交表の分散分析は「8つのルール」を理解すれば、どんな問題でも解けるようになります。
この記事では、2水準系直交表(L4・L8・L16など)の分散分析について、基礎から推定まで完全解説します。QC検定1級レベルの内容を、図解と例題で丁寧に説明していきますので、ぜひ最後まで読んでください。
目次
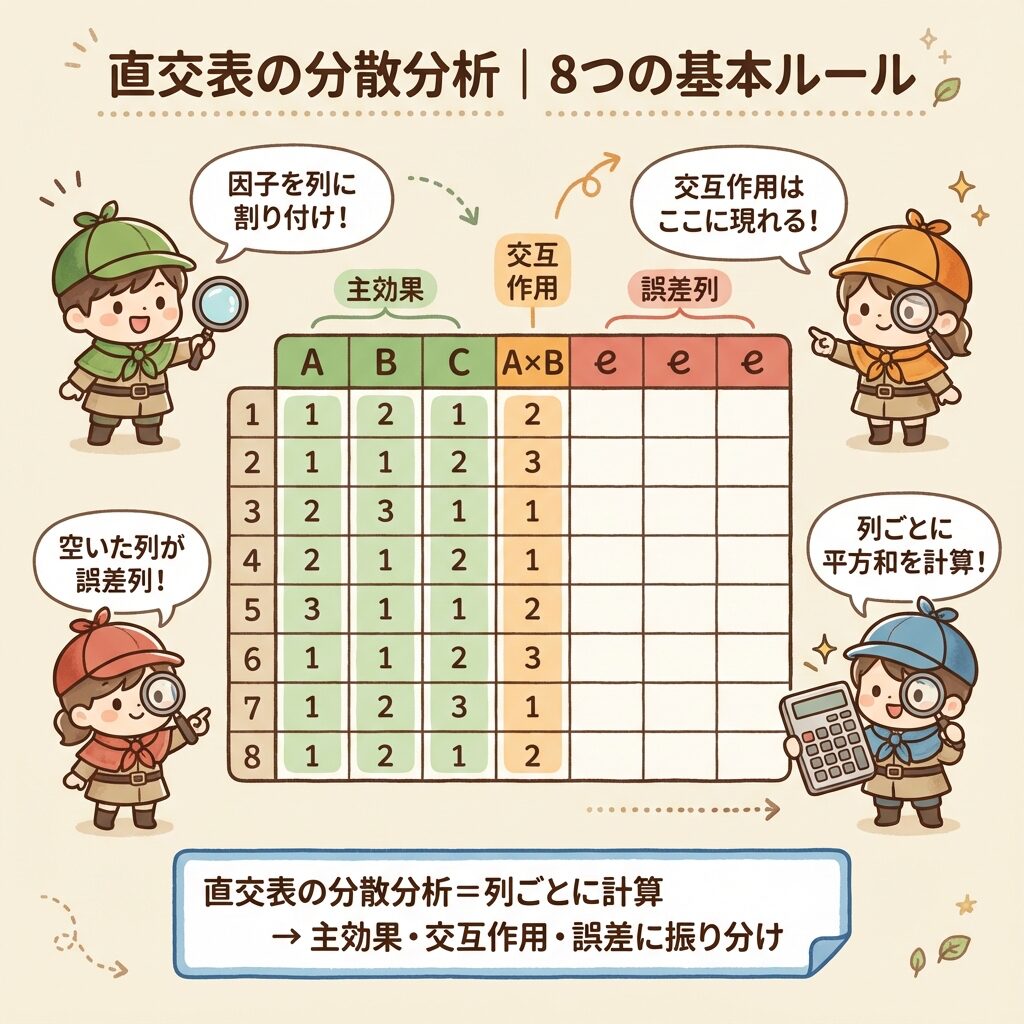
2水準系直交表の分散分析|8つの基本ルール
まずは、2水準系直交表の分散分析における8つの基本ルールを確認しましょう。これが理解できれば、計算の流れが見えてきます。
📋 2水準系直交表の分散分析|8つのルール
① 因子の割り付け
各列に因子の名前(A, B, Cなど)を割り付ける
② 水準の組合せ
因子を割り付けることで、実験を実施する各因子の水準組合せがわかる
(表中の1, 2は水準番号を表す)
③ 誤差列の特定
因子が割り付けられておらず、また取り上げた交互作用が現われない列は「誤差列」とする
④ 列平方和の計算
各列の平方和を求める。各列の平方和を「列平方和」という
⑤ 主効果の平方和
因子の主効果の平方和と自由度は、その因子を割り付けた列の平方和と自由度になる
⑥ 交互作用の平方和
交互作用の平方和と自由度は、その交互作用が現われる列の平方和と自由度になる
⑦ 誤差平方和
誤差平方和 SE は誤差列の平方和の和で、誤差自由度 φE は誤差列の自由度の和となる
⑧ 総平方和
総平方和 ST はすべての列の平方和の合計に等しい。総自由度 φT はすべての列の自由度の合計に等しい
特に重要なのは③の「誤差列」です。一元配置や二元配置では「繰返し」から誤差を求めましたが、直交表では「使わない列」が誤差になるという独特のルールがあります。
なぜ「列ごと」に計算するのか?
直交表の最大の特徴は、「各列が直交している」ことです。
直交しているとは、各列が互いに独立していること。つまり、ある列の効果が、他の列の効果に影響を与えないということです。
この性質があるからこそ、私たちは「列ごとに」平方和を計算できるのです。一元配置や二元配置と同じように、各因子の効果を独立して評価できるのが直交表の強みです。
直交表の分散分析 = 「列ごとに平方和を求めて、それを主効果・交互作用・誤差に振り分ける」という作業です。
列平方和の求め方|2つの公式を使い分ける
直交表の分散分析で最も重要な計算が「列平方和」の計算です。
列平方和を求める公式は2つあります。どちらを使っても同じ答えになりますが、2水準系では「簡便式」を使うと計算がラクになります。
公式①:一般式(多水準でも使える)
まずは、一元配置や二元配置と同じ考え方の「一般式」です。
この式は、一元配置の「水準間平方和」と同じ形です。各水準のデータ合計を2乗して、データ数で割り、修正項CTを引く。
多水準(3水準以上)の直交表を使う場合は、この一般式を使います。
公式②:簡便式(2水準専用)
2水準系の直交表(L4・L8・L16など)では、より簡単な公式が使えます。
T[k]1:第[k]列の第1水準のデータ和
T[k]2:第[k]列の第2水準のデータ和
N:総データ数
この簡便式は、「第1水準の合計と第2水準の合計の差を2乗して、総データ数で割るだけ」です。修正項CTを引く必要がないので、計算がとても簡単になります。
なぜ簡便式が成り立つのか?
2水準の場合、第1水準のデータ数と第2水準のデータ数は常に等しくなります(どちらもN/2個)。
一般式に代入して整理すると…
S[k] = T[k]1²/(N/2) + T[k]2²/(N/2) − (T[k]1 + T[k]2)²/N
= 2(T[k]1² + T[k]2²)/N − (T[k]1 + T[k]2)²/N
= {2(T[k]1² + T[k]2²) − (T[k]1 + T[k]2)²}/N
= {2T[k]1² + 2T[k]2² − T[k]1² − 2T[k]1T[k]2 − T[k]2²}/N
= (T[k]1² − 2T[k]1T[k]2 + T[k]2²)/N = (T[k]1 − T[k]2)²/N
このように、2水準の場合に限り、簡便式が成り立ちます。QC検定ではこの簡便式を使うと計算ミスが減るので、ぜひ覚えてください。
列の自由度
各列の自由度(列自由度)φ[k]は、水準数 − 1 です。
2水準系の場合:φ[k] = 2 − 1 = 1(すべての列で自由度は1)
2水準系の直交表では、すべての列の自由度が1になります。これは覚えておくと便利です。

誤差列の見つけ方|直交表特有のルール
直交表の分散分析で、最も理解しにくいのが「誤差列」の概念です。
一元配置や二元配置では、「繰返し」から誤差を計算しました。しかし、直交表では繰返しがない場合も多いです。では、誤差はどこから求めるのでしょうか?
誤差列とは?
直交表には複数の「列」がありますが、すべての列に因子を割り付けるわけではありません。
因子が割り付けられておらず、かつ取り上げた交互作用が現われない列を「誤差列」とする
つまり、誤差列とは「何の効果も表していない列」のことです。この列の変動は、純粋な「バラつき(誤差)」と見なせます。
【具体例】L8直交表での誤差列
L8直交表には7つの列があります。ここに3因子(A, B, C)を割り付ける場合を考えてみましょう。
| 列番号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 割り付け | A | B | A×B | C | e | e | e |
| 役割 | 主効果 | 主効果 | 交互作用 | 主効果 | 誤差列 | 誤差列 | 誤差列 |
この例では、A×Bの交互作用を取り上げているため、第3列は交互作用列になります。第5・6・7列は、因子も交互作用も割り付けられていないので、「誤差列」となります。
誤差平方和と誤差自由度の計算
誤差平方和と誤差自由度は、誤差列の平方和・自由度を合計して求めます。
φE = φ[5] + φ[6] + φ[7] = 1 + 1 + 1 = 3(誤差列の自由度の和)
2水準系では各列の自由度が1なので、誤差列が3つあれば誤差自由度は3になります。
交互作用を取り上げない場合は、その交互作用が現われる列も誤差列になります。上の例でA×Bを取り上げなければ、第3列も誤差列となり、誤差自由度は4になります。
総平方和の検算
直交表の便利な性質として、「総平方和 = すべての列平方和の合計」が成り立ちます。
φT = φ[1] + φ[2] + ... + φ[7] = 7(L8の場合)
この関係を使うと、計算の検算ができます。総平方和を直接計算した値と、列平方和の合計が一致すれば、計算が正しいことが確認できます。
【実践】L8直交表の分散分析を計算する
ここからは、具体的な例題を使って、L8直交表の分散分析を実際に計算してみましょう。
例題の設定
📝 例題
ある製品の強度を向上させるため、3つの因子(A:温度、B:時間、C:材料)について、L8直交表を用いて実験を行った。各因子は2水準とし、以下の結果を得た。A×Bの交互作用を取り上げる。
| 実験No. | 列1 A |
列2 B |
列3 A×B |
列4 C |
列5 e |
列6 e |
列7 e |
データy |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 12 |
| 2 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 14 |
| 3 | 1 | 2 | 2 | 1 | 1 | 2 | 2 | 18 |
| 4 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 20 |
| 5 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 22 |
| 6 | 2 | 1 | 2 | 2 | 1 | 2 | 1 | 24 |
| 7 | 2 | 2 | 1 | 1 | 2 | 2 | 1 | 26 |
| 8 | 2 | 2 | 1 | 2 | 1 | 1 | 2 | 28 |
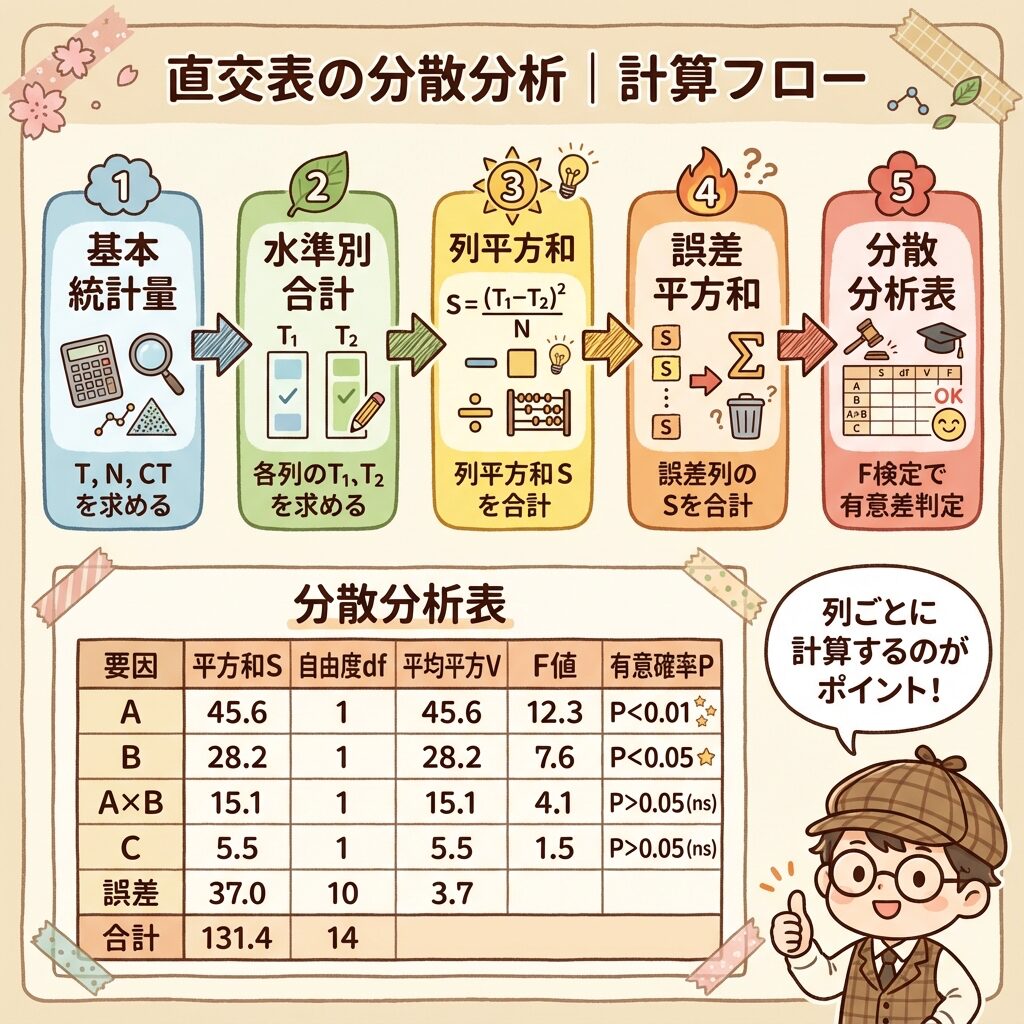
ステップ①:基本統計量の計算
まず、計算に必要な基本統計量を求めます。
データの総和 T = 12 + 14 + 18 + 20 + 22 + 24 + 26 + 28 = 164
総データ数 N = 8
修正項 CT = T²/N = 164²/8 = 26896/8 = 3362
ステップ②:各列の水準別合計を求める
次に、各列について「第1水準のデータ合計」と「第2水準のデータ合計」を求めます。
| 列 | 割り付け | T[k]1 (水準1の合計) |
T[k]2 (水準2の合計) |
差 T[k]1−T[k]2 |
|---|---|---|---|---|
| 1 | A | 12+14+18+20=64 | 22+24+26+28=100 | −36 |
| 2 | B | 12+14+22+24=72 | 18+20+26+28=92 | −20 |
| 3 | A×B | 12+14+26+28=80 | 18+20+22+24=84 | −4 |
| 4 | C | 12+18+22+26=78 | 14+20+24+28=86 | −8 |
| 5 | e | 12+18+24+28=82 | 14+20+22+26=82 | 0 |
| 6 | e | 12+20+22+26=80 | 14+18+24+28=84 | −4 |
| 7 | e | 12+20+24+26=82 | 14+18+22+28=82 | 0 |
ステップ③:列平方和を計算する(簡便式)
2水準系なので、簡便式 S[k] = (T[k]1 − T[k]2)² / N を使います。
S[1] = (−36)² / 8 = 1296 / 8 = 162 (因子A)
S[2] = (−20)² / 8 = 400 / 8 = 50 (因子B)
S[3] = (−4)² / 8 = 16 / 8 = 2 (A×B)
S[4] = (−8)² / 8 = 64 / 8 = 8 (因子C)
S[5] = (0)² / 8 = 0 / 8 = 0 (誤差列)
S[6] = (−4)² / 8 = 16 / 8 = 2 (誤差列)
S[7] = (0)² / 8 = 0 / 8 = 0 (誤差列)
ステップ④:誤差平方和を計算する
誤差列(第5・6・7列)の平方和を合計します。
SE = S[5] + S[6] + S[7] = 0 + 2 + 0 = 2
φE = 1 + 1 + 1 = 3
ステップ⑤:分散分析表を完成させる
以上の結果をまとめて、分散分析表を作成します。
| 要因 | 平方和 S | 自由度 φ | 分散 V | F値 | 判定 |
|---|---|---|---|---|---|
| A | 162 | 1 | 162.00 | 243.00 | ** |
| B | 50 | 1 | 50.00 | 75.00 | ** |
| A×B | 2 | 1 | 2.00 | 3.00 | |
| C | 8 | 1 | 8.00 | 12.00 | * |
| 誤差 e | 2 | 3 | 0.67 | − | − |
| 計 T | 224 | 7 | − | − | − |
F分布表の値(φ1=1, φ2=3):F(1,3;0.05) = 10.13、F(1,3;0.01) = 34.12
この結果から、因子AとBは1%水準で有意(**)、因子Cは5%水準で有意(*)、A×Bの交互作用は有意でないことがわかります。
母平均の点推定|最適条件での予測値を求める
分散分析で有意な因子がわかったら、次は「最適条件を決めて、そのときの母平均を推定する」ステップに進みます。
最適条件の決定
望大特性(大きいほど良い)の場合、各因子の平均値が大きい水準を選びます。
| 因子 | 水準1の平均 | 水準2の平均 | 最適水準 |
|---|---|---|---|
| A | 64/4 = 16 | 100/4 = 25 | A₂ |
| B | 72/4 = 18 | 92/4 = 23 | B₂ |
| C | 78/4 = 19.5 | 86/4 = 21.5 | C₂ |
したがって、最適条件はA₂B₂C₂となります。
母平均の点推定
最適条件A₂B₂C₂における母平均μの点推定値μ̂は、以下の式で求めます。
= Ā₂ + B̄₂ + C̄₂ − 2x̄
x̄:全体平均 | Ā₂, B̄₂, C̄₂:各因子の最適水準の平均
計算してみましょう。
全体平均 x̄ = 164 / 8 = 20.5
Ā₂ = 100 / 4 = 25
B̄₂ = 92 / 4 = 23
C̄₂ = 86 / 4 = 21.5
μ̂ = 25 + 23 + 21.5 − 2 × 20.5 = 69.5 − 41 = 28.5
最適条件A₂B₂C₂で製造した場合、強度の母平均は28.5と推定されます。
点推定値の分散の推定|有効繰返し数を使う
点推定値μ̂がわかったら、次に「その推定値がどのくらい信頼できるか」を評価します。それが「点推定値の分散」です。
有効繰返し数 ne とは?
直交表では実際の「繰返し」がないため、「仮想的な繰返し数」として有効繰返し数 ne を使います。
N:総データ数 | 点推定に使った自由度 = 有意な因子の自由度の合計
今回の例では、A・B・Cの3因子を点推定に使っています(各自由度1)。
ne = 8 / (1 + 1 + 1 + 1) = 8 / 4 = 2
点推定値の分散
点推定値μ̂の分散は、以下の式で推定します。
VE:誤差分散 | ne:有効繰返し数
V(μ̂) = VE / ne = 0.67 / 2 = 0.33
母平均の区間推定(信頼区間)
点推定値の分散がわかれば、95%信頼区間を計算できます。
t(3, 0.05) = 3.182(t分布表より)
√V(μ̂) = √0.33 = 0.58
信頼区間 = 28.5 ± 3.182 × 0.58 = 28.5 ± 1.85
26.65 ≦ μ ≦ 30.35
最適条件A₂B₂C₂における母平均μは、95%の信頼度で26.65〜30.35の範囲にあると推定されます。

