😰 こんな経験、ありませんか?
- F検定をしたら「等分散でない」と出た…どうすれば?
- 2群を比較したいのに、バラつきが全然違う…
- 「スチューデントのt検定は使えません」と言われた…
- そもそもウェルチって誰?何が違うの?
💡 この記事の結論
ウェルチのt検定は、2つのグループのバラつき(分散)が異なる場合でも平均値の差を検定できる手法です。
「スチューデントのt検定」が等分散を前提とするのに対し、ウェルチのt検定は前提なしで使える「万能選手」です。
📚 この記事でわかること
- ウェルチのt検定が必要になる場面と理由
- スチューデントのt検定との違い(図解つき)
- 自由度の計算方法(ウェルチ-サタスウェイトの近似式)
- 具体的な計算例(手計算できるレベルで)
目次
なぜウェルチのt検定が必要なのか?
前回の記事で学んだ「スチューデントのt検定」は、2つのグループの平均を比較する強力な手法でした。
しかし、この検定には大前提がありましたよね。
⚠️ スチューデントのt検定の前提条件
「2つのグループの母分散が等しい」こと
でも、現実のデータはそんなに都合よくありません。
たとえば、こんなケースを想像してみてください。

🏭 例:2つの工場の品質比較
状況:同じ製品を作る2つの工場の品質を比較したい。
| 工場 | 平均寸法 | バラつき(分散) | 特徴 |
|---|---|---|---|
| A工場 | 50.2 mm | 1.5 | ベテラン職人が多く安定 |
| B工場 | 51.8 mm | 8.2 | 新人が多くバラつき大 |
→ 分散が 1.5 vs 8.2 で全然違う!等分散とは言えない…
このように、バラつきの大きさが違う2つのグループを比較したい場面は、実務では頻繁に発生します。
🎯 イメージで理解する:的当てゲームで考えよう
🎯 2人の選手が的当てをする場面
選手A(ベテラン)
🎯
的の中心付近に
密集して当たる
バラつき:小
選手B(初心者)
🎯
的のあちこちに
散らばって当たる
バラつき:大
この2人の「平均的な的中位置」を比較したい場合、単純に「同じ尺度」で測っていいでしょうか?
選手Aの「5cm外れた」と、選手Bの「5cm外れた」は意味が違いますよね。
選手Aにとっては大きなミス、選手Bにとってはいつも通り。
ウェルチのt検定は、この「バラつきの違い」を考慮して、フェアに比較できる手法なのです。
スチューデント vs ウェルチ:何が違う?
2つのt検定の違いを、表でスッキリ整理しましょう。
| 比較項目 | スチューデントのt検定 | ウェルチのt検定 |
|---|---|---|
| 等分散の前提 | 必要 | 不要 |
| 分散の扱い | プールして1つにまとめる | 各群の分散をそのまま使う |
| 自由度の計算 | シンプル(n₁ + n₂ − 2) | 複雑(近似式を使用) |
| 検出力 | 等分散なら高い | やや低い(保守的) |
| 使う場面 | F検定で等分散が確認できた時 | 等分散かわからない/違う時 |
💡 実務でのポイント
最近の統計ソフトでは、「迷ったらウェルチを使え」という考え方が主流です。
等分散の場合でもウェルチのt検定は使えますし、結果も大きくは変わりません。
安全策として、常にウェルチを使う研究者も多いです。

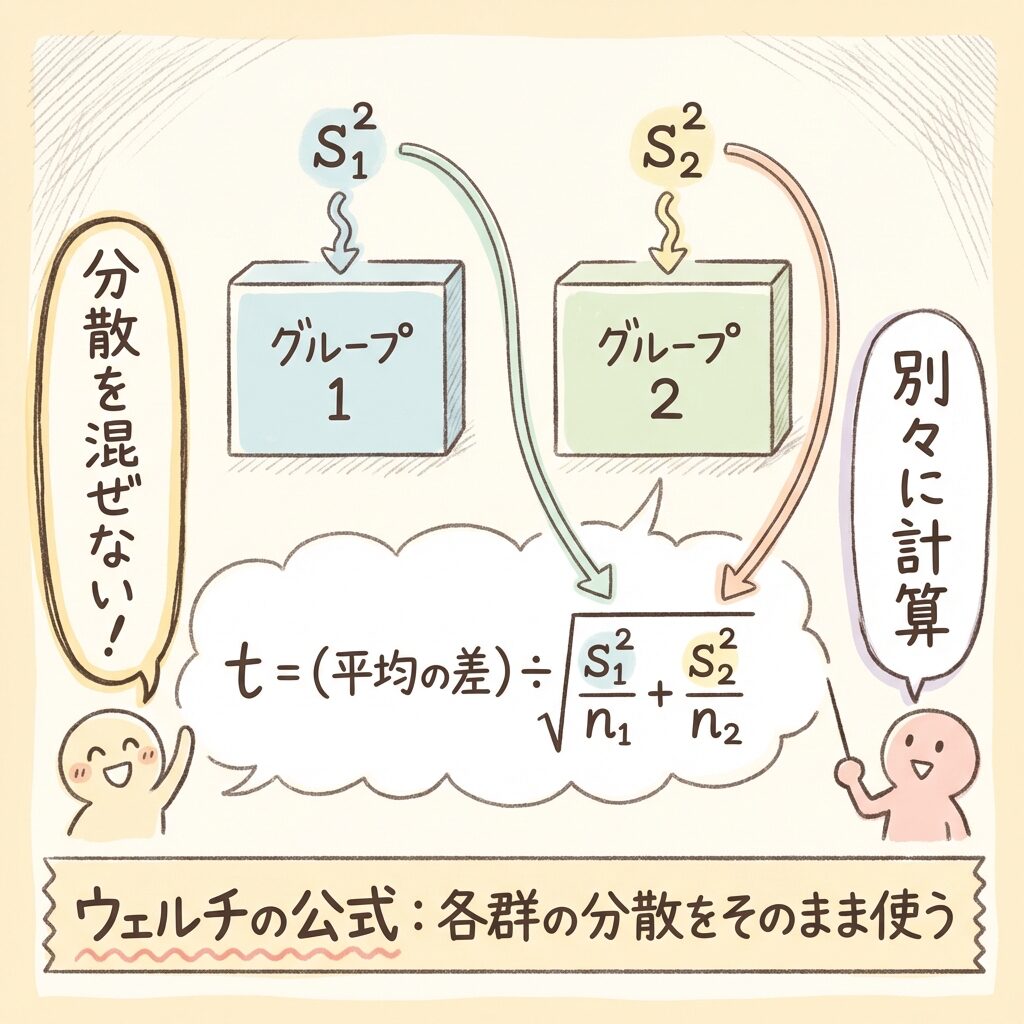
ウェルチのt検定の公式
📐 t値の計算式
t = (x̄₁ − x̄₂) ÷ √(s₁²/n₁ + s₂²/n₂)
各記号の意味を確認しましょう。
| 記号 | 意味 |
|---|---|
| x̄₁, x̄₂ | 各グループの標本平均 |
| s₁², s₂² | 各グループの不偏分散 |
| n₁, n₂ | 各グループのサンプルサイズ |
🔍 スチューデントのt検定との違い
スチューデントのt検定では、分母に「プールした分散」を使いました。
ウェルチのt検定では、各群の分散をそのまま別々に計算に使います。
「混ぜないで、それぞれの個性を尊重する」イメージです。
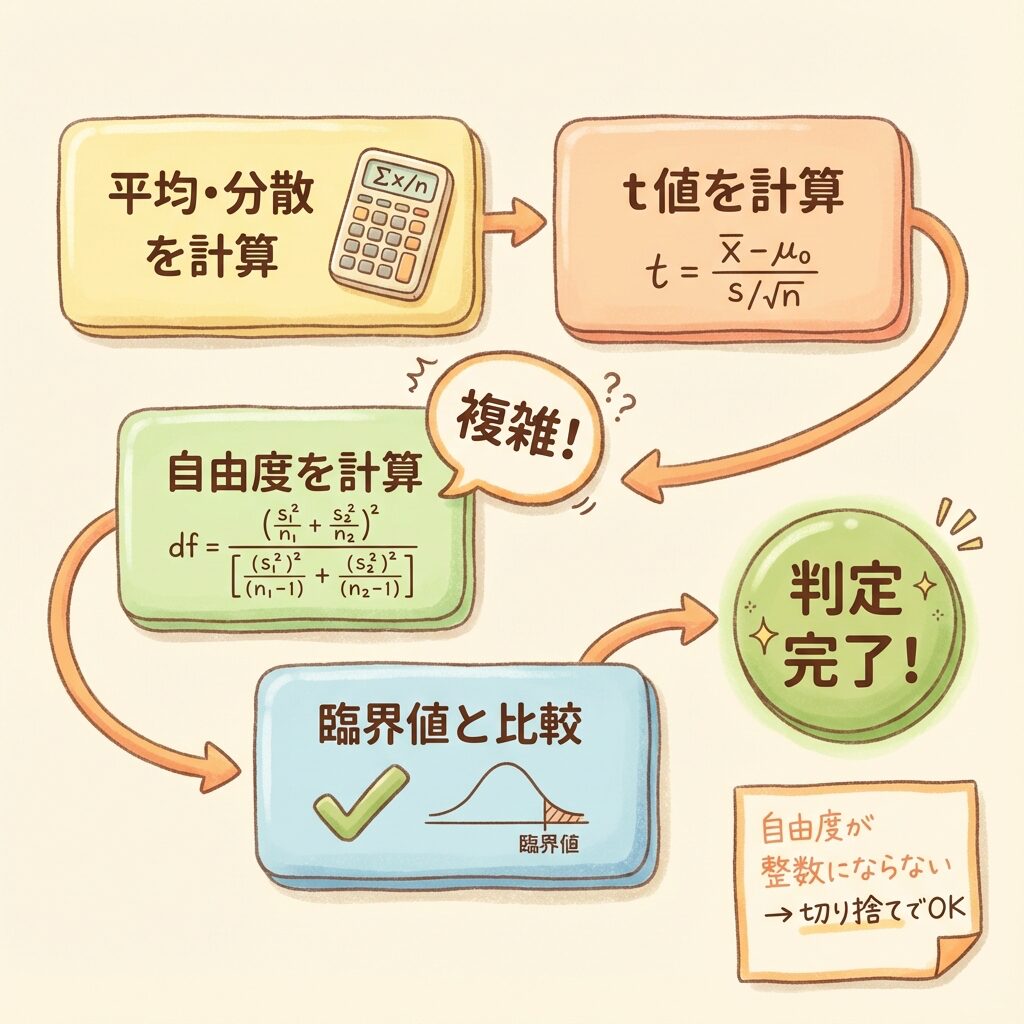
🧮 自由度の計算(ウェルチ-サタスウェイトの近似式)
ここがウェルチのt検定の最大の特徴であり、難しいポイントです。
通常のt検定では自由度は「n₁ + n₂ − 2」という単純な式でしたが、ウェルチのt検定では複雑な近似式を使います。
📊 ウェルチ-サタスウェイトの自由度
df ≈ (s₁²/n₁ + s₂²/n₂)² ÷ [(s₁²/n₁)²/(n₁−1) + (s₂²/n₂)²/(n₂−1)]
式が複雑に見えますが、心配しないでください。
この計算はExcelや統計ソフトが自動でやってくれます。大切なのは「なぜ複雑になるか」を理解することです。
🤔 なぜ自由度が複雑になるのか?(イメージで理解)
🎒 例え話:2人の荷物の重さを比べる
スチューデントのt検定:
「2人の荷物は同じ種類のものが入っている」と仮定。
だから、荷物を全部まとめて平均的な重さを計算できる。
自由度の計算も単純。
ウェルチのt検定:
「2人の荷物には違う種類のものが入っているかも」と考える。
Aさんの荷物の重さのバラつきと、Bさんの荷物の重さのバラつきを別々に考慮する必要がある。
その「別々に考慮する」処理が、自由度の式を複雑にしている。
⚠️ 重要なポイント
ウェルチの自由度は、整数にならないことが多いです(例:df = 12.7)。
t分布表を使う場合は、小数点以下を切り捨てて保守的に判定します。
統計ソフトを使えば、小数のまま正確に計算してくれます。
【具体例】ウェルチのt検定を手計算してみよう
📋 ケーススタディ:2つの工場の製品比較
🏭 設定
A工場とB工場で作られた部品の平均寸法に差があるかを検定します。
F検定の結果、等分散でないことがわかりました。
そのため、ウェルチのt検定を使います。
有意水準 α = 0.05(両側検定)とします。
📊 測定データ
| 工場 | 測定値(mm) |
|---|---|
| A工場(n₁=6) | 50, 51, 50, 51, 50, 50 |
| B工場(n₂=6) | 48, 54, 47, 55, 52, 50 |
📝 STEP 1:基本統計量を計算
| 統計量 | A工場 | B工場 |
|---|---|---|
| サンプルサイズ n | 6 | 6 |
| 標本平均 x̄ | 50.33 mm | 51.00 mm |
| 不偏分散 s² | 0.27 | 10.00 |
👀 注目ポイント
不偏分散を見てください。0.27 vs 10.00で約37倍も違います!
これが「等分散でない」状態です。
A工場は安定、B工場はバラバラ。この状況でスチューデントのt検定を使うのは不適切です。
📝 STEP 2:t値を計算
公式:t = (x̄₁ − x̄₂) ÷ √(s₁²/n₁ + s₂²/n₂)
分子:50.33 − 51.00 = −0.67
分母:√(0.27/6 + 10.00/6) = √(0.045 + 1.667) = √1.712 ≈ 1.31
t = −0.67 ÷ 1.31 ≈ −0.51
📝 STEP 3:自由度を計算(ウェルチ-サタスウェイト)
ここが複雑な部分ですが、順番に計算していきましょう。
A = s₁²/n₁ = 0.27/6 = 0.045
B = s₂²/n₂ = 10.00/6 = 1.667
分子:(A + B)² = (0.045 + 1.667)² = 1.712² = 2.93
分母:A²/(n₁−1) + B²/(n₂−1)
= 0.045²/5 + 1.667²/5
= 0.0004 + 0.556 = 0.556
df = 2.93 ÷ 0.556 ≈ 5.27
自由度が整数にならない点に注目してください。これがウェルチのt検定の特徴です。
t分布表を使う場合は、切り捨てて df = 5 として判定します。
📝 STEP 4:判定
| 項目 | 値 |
|---|---|
| 計算したt値 | −0.51(絶対値 0.51) |
| 自由度 | 5(5.27を切り捨て) |
| 臨界値(α=0.05, 両側) | 2.571 |
📊 判定結果
|t| = 0.51 < 臨界値 2.571
→ 帰無仮説を棄却できない
📝 結論の書き方
「ウェルチのt検定を行った結果、A工場とB工場の製品の平均寸法に有意な差は認められなかった(t = −0.51, df = 5.27, p > 0.05)。
ただし、B工場は分散が大きく品質の安定性に課題がある可能性があり、別途検討が必要である。」
実務での注意点とよくある誤解
⚠️ よくある誤解
❌ 誤解1:「等分散ならウェルチは使えない」
正解:等分散の場合でもウェルチのt検定は使えます。
結果はスチューデントのt検定とほぼ同じになります。
むしろ、「迷ったらウェルチ」が現代の主流です。
❌ 誤解2:「ウェルチの方が常に正確」
正解:ウェルチのt検定は「安全」ですが、等分散が明らかな場合はスチューデントのt検定の方が検出力(Power)が高いです。
つまり、差があるときに「差がある」と見抜く力が強いということです。
❌ 誤解3:「F検定で有意でなければスチューデントでOK」
正解:F検定で「有意でない」≠「等分散が証明された」です。
サンプルサイズが小さいと、本当は分散が違っても検出できないことがあります。
不安な場合は、ウェルチを使う方が安全です。
🔧 実務でのフローチャート
📋 2群の平均を比較するときの判断フロー
① 対応があるか?
→ Yes:対応のあるt検定
→ No:②へ
② F検定で等分散を確認
→ 等分散:スチューデントのt検定
→ 等分散でない:ウェルチのt検定
→ よくわからない:ウェルチのt検定(安全策)
まとめ:ウェルチのt検定のポイント
| 使う場面 | 2群の平均を比較したいが、分散が異なる(または不明な)とき |
| 前提条件 | 正規性は必要。等分散は不要 |
| 特徴 | 各群の分散を別々に使う。自由度の計算が複雑 |
| 実務のコツ | 迷ったらウェルチを選べば安全 |
💡 覚え方のコツ
「ウェルチ」=「Well Check(よく確認)」
バラつきが違っても「よく確認」して比較できる、安全な検定方法!
📖 NEXT STEP
次に学ぶべきは「対応のあるt検定」
同じ人のビフォー・アフターを比較したい場合は、また別の検定が必要です。
「個人差」という厄介な変動を消し去る最強の方法を学びましょう。
🎉
お疲れ様でした!
ウェルチのt検定は、実務で最も安全に使える2群比較の方法です。
「迷ったらウェルチ」を合言葉に、自信を持って分析を進めてください。
関連記事
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


