🤔 こんな疑問、ありませんか?
- 「平均は50.5mmです」って言われたけど、どのくらい信頼できるの?
- 「95%信頼区間」ってよく聞くけど、何が95%なの?
- 検定と推定って何が違うの?
- 区間推定の計算方法を具体的に知りたい…
💡 この記事の結論
区間推定とは、「真の平均値(母平均)はこの範囲のどこかにある」と幅を持たせて推定する方法です。
「50.5mmです!」と言い切るより、「48.2〜52.8mmの間です」と言う方が誠実で科学的。
この「幅」を計算するのが区間推定です。
📚 この記事でわかること
- 「点推定」と「区間推定」の違い
- 「95%信頼区間」の正しい解釈(よくある誤解を解消)
- 母平均の区間推定の計算公式と具体例
- 検定と推定の使い分け
目次
なぜ「区間」で推定するのか?
まず、点推定と区間推定の違いを理解しましょう。
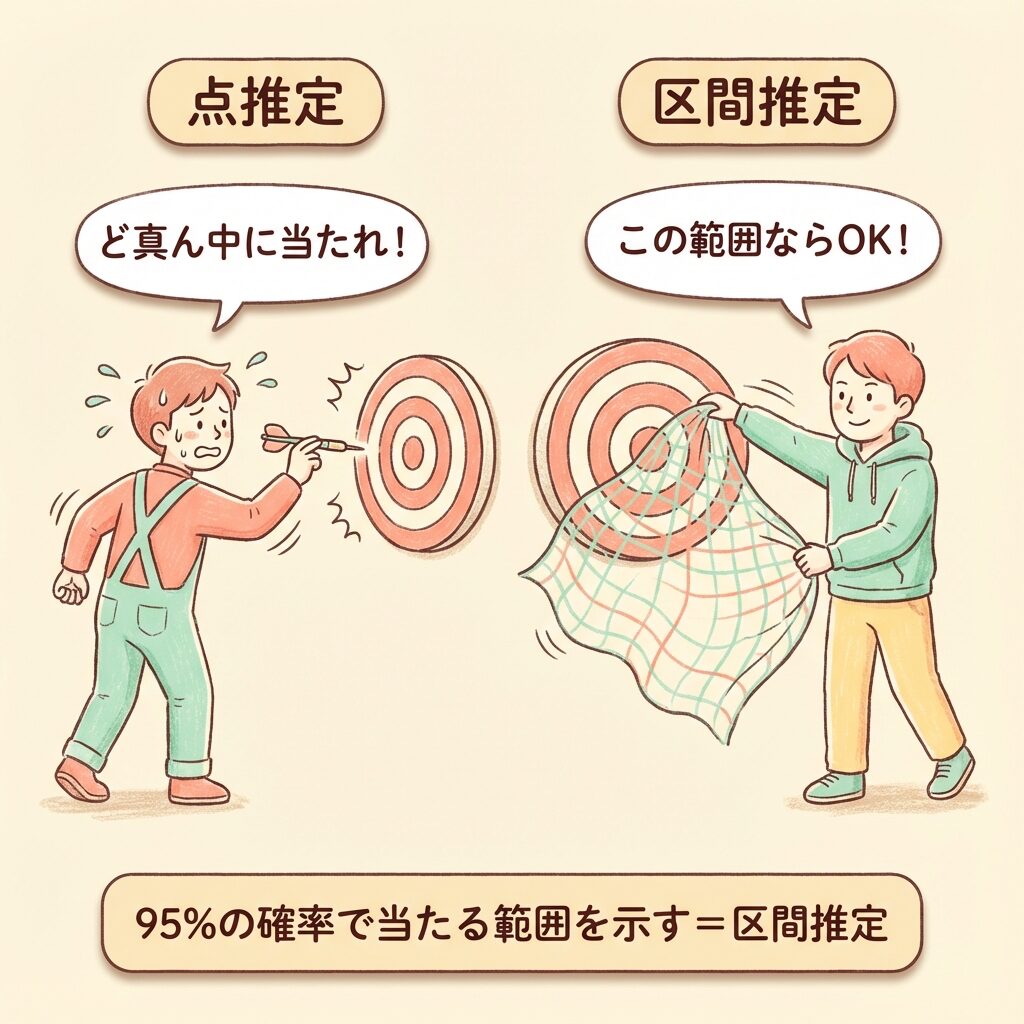
🎯 例え話:的当てゲームで考える
友達が「真ん中に当たった!」と主張しています。
でも、あなたは的を見ていませんでした。
点推定
🎯
「ど真ん中に当たった!」
と言い切る
外れてたら恥ずかしい…
区間推定
🎯
「この範囲のどこかに
当たった」と幅を持たせる
外れにくい!誠実!
→ 区間推定は「外れにくい予測」ができる誠実な方法なのです。
📊 統計学での「点推定」と「区間推定」
| 比較項目 | 点推定 | 区間推定 |
|---|---|---|
| 表現方法 | 「母平均は50.5です」 | 「母平均は48.2〜52.8の間です」 |
| 使う値 | 標本平均 x̄ のみ | x̄ ± t × 標準誤差 |
| 信頼度 | 不明(当たるかどうかは運次第) | 明示できる(95%など) |
| メリット | シンプル・わかりやすい | 不確実性を含めて表現できる |
| デメリット | 「どのくらい正確か」がわからない | 計算がやや複雑 |
💡 ポイント
点推定は「当たるかどうかわからない1点」。
区間推定は「95%の確率で当たる範囲」。
科学論文やビジネスレポートでは、区間推定の方が信頼されるのはこのためです。
「95%信頼区間」の正しい解釈
ここで、最もよくある誤解を解消しておきましょう。
❌ よくある誤解
誤った解釈
「95%信頼区間が48.2〜52.8ということは、
母平均が48.2〜52.8の間にある確率が95%である」
→ これは間違いです!
✅ 正しい解釈
正しい解釈
「同じ方法で100回調査したら、
そのうち95回は真の母平均を含む区間が得られる」
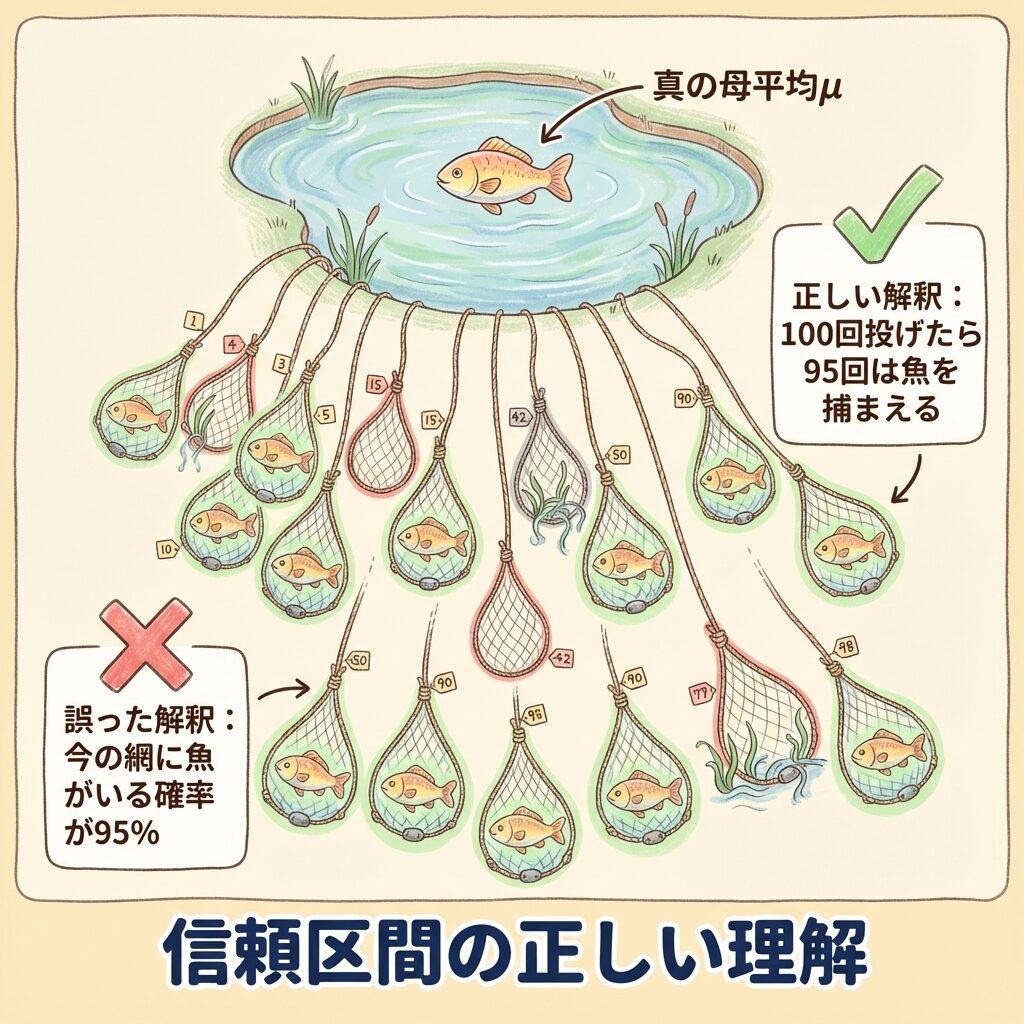
🎣 例え話:釣りで考える
池にいる魚(母平均)を網(信頼区間)で捕まえようとしています。
誤った考え方:「今投げた網の中に魚がいる確率が95%」
→ 魚は決まった場所にいる。網の中にいるか、いないかの2択。確率ではない。
正しい考え方:「この方法で100回網を投げたら、95回は魚が入る」
→ 網の投げ方(推定方法)の信頼性が95%ということ。
🧠 つまり…
母平均(真の値)は固定された1つの値です。動きません。
動くのは私たちが計算する信頼区間の方です。
100回調査すれば100個の異なる信頼区間ができますが、
そのうち95個は真の母平均を含んでいる…というのが正しい解釈です。
母平均の区間推定の公式
📐 公式(母分散が未知の場合)
95%信頼区間の公式
x̄ − t × (s/√n) ≦ μ ≦ x̄ + t × (s/√n)
各記号の意味を確認しましょう。
| 記号 | 意味 |
|---|---|
| x̄ | 標本平均(サンプルの平均値) |
| μ | 母平均(推定したい真の値) |
| s | 標本標準偏差(不偏分散の平方根) |
| n | サンプルサイズ(データの個数) |
| t | t分布の臨界値(自由度n-1、信頼度に対応) |
| s/√n | 標準誤差(Standard Error, SE) |
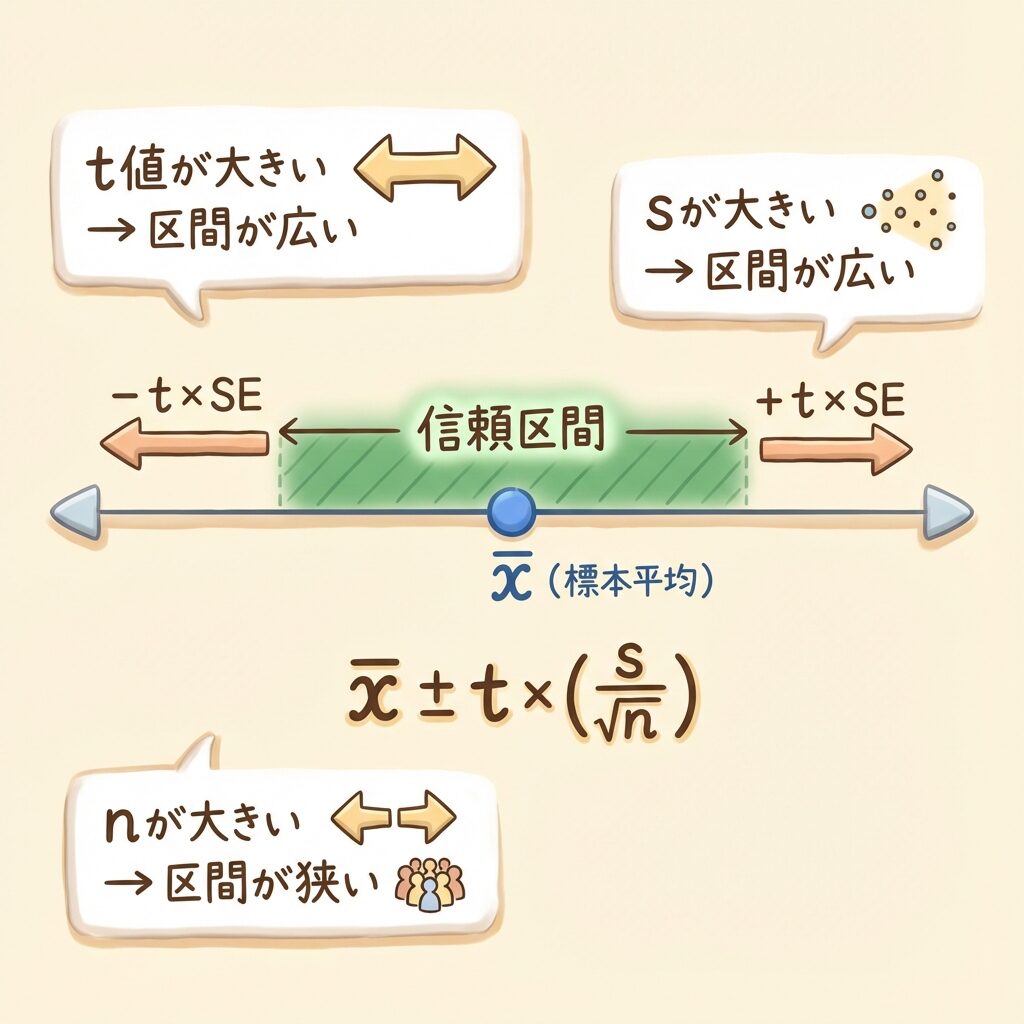
🎯 公式のイメージ
📏 信頼区間 = 標本平均 ± 「のりしろ」
x̄ ± t × (s/√n)
↑中心 ↑のりしろ(マージン)
中心:標本平均 x̄(「ここだろう」という最良の推定値)
のりしろ:t × 標準誤差(「でも、これくらいズレるかも」という余裕)
🔍 「のりしろ」を決める3つの要素
① t値(信頼度)
95%信頼区間なら t は約2。99%信頼区間なら t は約2.6。
信頼度を上げる → t値が大きくなる → 区間が広くなる
② s(標準偏差)
データのバラつきが大きい → s が大きい → 区間が広くなる
バラつきが大きいほど、推定の不確実性が増す
③ n(サンプルサイズ)
サンプル数が多い → √n が大きい → 区間が狭くなる
データが多いほど、推定の精度が上がる
標準偏差と標準誤差の違いは?「ポテトチップス」で解説 →
【計算例】部品の平均寸法を推定する
📋 問題設定
🔧 製造部品の品質管理
ある工場で製造している部品の母平均(真の平均寸法)を推定したい。
10個の部品をランダムに抽出して測定したところ、以下のデータが得られました。
95%信頼区間を求めてください。
📊 測定データ(単位:mm)
50.2, 49.8, 50.5, 50.1, 49.9, 50.3, 50.0, 50.4, 49.7, 50.1
📝 STEP 1:標本平均 x̄ を計算
合計:50.2 + 49.8 + 50.5 + 50.1 + 49.9 + 50.3 + 50.0 + 50.4 + 49.7 + 50.1 = 501.0
x̄ = 501.0 ÷ 10 = 50.10 mm
📝 STEP 2:標本標準偏差 s を計算
各データと平均の偏差の2乗を計算し、合計します。
| データ x | x − x̄ | (x − x̄)² |
|---|---|---|
| 50.2 | 0.1 | 0.01 |
| 49.8 | −0.3 | 0.09 |
| 50.5 | 0.4 | 0.16 |
| 50.1 | 0.0 | 0.00 |
| 49.9 | −0.2 | 0.04 |
| 50.3 | 0.2 | 0.04 |
| 50.0 | −0.1 | 0.01 |
| 50.4 | 0.3 | 0.09 |
| 49.7 | −0.4 | 0.16 |
| 50.1 | 0.0 | 0.00 |
| 合計 | 0.60 | |
不偏分散 s² = 0.60 ÷ (10 − 1) = 0.60 ÷ 9 ≈ 0.0667
s = √0.0667 ≈ 0.258 mm
📝 STEP 3:標準誤差を計算
標準誤差 SE = s / √n = 0.258 / √10 = 0.258 / 3.162
SE ≈ 0.082 mm
📝 STEP 4:t値を確認
📝 STEP 5:信頼区間を計算
のりしろ = t × SE = 2.262 × 0.082 ≈ 0.185 mm
下限:50.10 − 0.185 = 49.915 mm
上限:50.10 + 0.185 = 50.285 mm
📊 結果
95%信頼区間:49.92 mm ≦ μ ≦ 50.29 mm
📝 結論の書き方
「10個の部品を測定した結果、標本平均は50.10 mmであった。
母平均の95%信頼区間は49.92〜50.29 mmと推定される。
この結果は、同様の調査を100回行った場合、約95回は真の母平均がこの区間に含まれることを意味する。」
P値と有意水準(α)|臨界値の読み方を理解する →

検定と推定の違い
⚖️ 「検定」と「推定」は兄弟のような関係
| 比較項目 | 検定 | 推定 |
|---|---|---|
| 目的 | 仮説が正しいか判定 | 値を推測する |
| 問いかけ | 「50mmと違うか?」 | 「何mmか?」 |
| 答え方 | Yes/No(有意差あり/なし) | 範囲(48.2〜52.8mm) |
| 使う場面 | 規格との比較、効果の有無 | 真の値を知りたいとき |
💡 実は裏表の関係!
95%信頼区間に「規格値50mm」が含まれていれば、検定でも「有意差なし」になります。
信頼区間に「規格値50mm」が含まれていなければ、検定でも「有意差あり」になります。
つまり、区間推定の結果から検定の結論もわかるのです!
まとめ:母平均の区間推定のポイント
| 区間推定とは | 母平均が「この範囲にある」と幅を持たせて推定する方法 |
| 95%の意味 | 100回調査したら95回は真の値を含む区間が得られる |
| 公式 | x̄ ± t × (s/√n) |
| 区間を狭くする | サンプルサイズ n を増やす / バラつき s を減らす |
💡 覚え方のコツ
「点推定」= ダーツの的の真ん中を狙う
「区間推定」= 的全体を網で覆う
網で覆えば95%の確率で的中!これが「誠実な推定」
📖 NEXT STEP
次に学ぶべきは「検出力とサンプルサイズ」
「n=10で実験したけど有意差なし」は計画ミスかも?
「差があるのに検出できなかった」を防ぐために、事前にサンプルサイズを決める方法を学びましょう。
これがわかれば、実験計画の精度が劇的に上がります。
🎉
お疲れ様でした!
区間推定は、「自分の分析結果にどれくらい自信があるか」を数値で示せる強力なツールです。
ビジネスでも論文でも、「95%信頼区間」が言えると説得力が格段に上がりますよ!
関連記事
統計学のおすすめ書籍
統計学の「数式アレルギー」を治してくれた一冊
「Σ(シグマ)や ∫(インテグラル)を見ただけで眠くなる…」 そんな私を救ってくれたのが、小島寛之先生の『完全独習 統計学入門』です。
この本は、難しい記号を一切使いません。 「中学レベルの数学」と「日本語」だけで、検定や推定の本質を驚くほど分かりやすく解説してくれます。
「計算はソフトに任せるけど、統計の『こころ(意味)』だけはちゃんと理解したい」 そう願う学生やエンジニアにとって、これ以上の入門書はありません。
【QC2級】「どこが出るか」がひと目で分かる!最短合格へのバイブル
私がQC検定2級に合格した際、使い倒したのがこの一冊です。
この本の最大の特徴は、「各単元の平均配点(何点分出るか)」が明記されていること。 「ここは出るから集中」「ここは出ないから流す」という戦略が立てやすく、最短ルートで合格ラインを突破できます。
解説が分かりやすいため、私はさらに上の「QC1級」を受験する際にも、基礎の確認用として辞書代わりに使っていました。 迷ったらまずはこれを選んでおけば間違いありません。


